Слободянюк А.И. Физика 10/11.8

Содержание книги

Предыдующая страница

§11. Постоянный электрический ток

11.8 Электрическое сопротивление среды при пространственно распределенных токах.

Электрический ток может протекать не только «концентрировано», по проводам. Движение электрических зарядов может занимать определенную область проводника, при этом векторное поле плотности тока \(~\vec j(x,y,z)\) , не обязательно является однородным, а представлять достаточно сложную структуру. Расчет электрического сопротивления между различными точками среды в этом случае принципиально отличается от рассмотренных выше. Особо отметим, что электрическое сопротивление среды зависит не только от ее свойств (удельного электрического сопротивления), но и от распределения токов в среде. Проиллюстрируем это положения двумя примерами, заодно и покажем методы расчета сопротивления для пространственно распределенных токов.

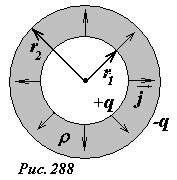
Пример 1. Пространство между двумя концентрическими хорошо проводящими сферами радиусами r₁ и r₂ заполнено слабопроводящим веществом с удельным электрическим сопротивлением ρ (рис. 288). Определим сопротивление среды между сферами.

Оговорки о проводимости сфер и среды между ними позволяют использовать следующие приближения:

- считать потенциалы сфер постоянными и пренебречь их сопротивлением;

- пренебречь объемными зарядами в пространстве между сферами, которые, в принципе, могут возникать при протекании электрического тока.

Для расчета сопротивления среды между сферами положим, что на внутренней сфере поддерживается постоянный электрический заряд +q (то есть сфера подключена к источнику тока, который компенсирует заряд, стекающий с него через проводящую среду). Электрическое поле в пространстве между сферами эквивалентно полю точечного заряда +q, помещенного в центр сфер. Следовательно, разность потенциалов между сферами может быть рассчитана по знакомой из электростатики формуле

\(~\Delta \varphi = \frac{q}{4 \pi \varepsilon_0} \left ( \frac{1}{r_1} - \frac{1}{r_2} \right )\) . (1)

Так как система обладает сферической симметрией, то вектор плотности электрического тока \(~\vec j\) во всех точках направлен радиально (вдоль прямой проходящей через центр сфер).

Задание для самостоятельной работы.

1. Докажите, что модуль вектора плотности тока убывает обратно пропорционально квадрату расстояния до центра сфер.

Непосредственно у поверхности внутренней сферы напряженность электрического поля равна

\(~E = \frac{q}{4 \pi \varepsilon_0 r^2_1}\) . (2)

По закону Ома плотность тока у поверхности сферы равна

\(~j = \frac{1}{\rho} E = \frac{q}{4 \pi \varepsilon_0 \rho r^2_1}\) . (3)

Так как вектор плотности тока направлен радиально, то есть по нормали к поверхности сферы, и постоянен по модулю, то сила электрического тока, стекающего со сферы, равная потоку вектора плотности тока, равна произведению плотности тока на площадь сферы \(~I = jS = \frac{1}{\rho} E = \frac{q}{4 \pi \varepsilon_0 \rho r^2_1} \cdot 4 \pi r^2_1 = \frac{q}{\varepsilon_0 \rho}\) . Зная силу тока и разность потенциала, электрическое сопротивление рассматриваемой системы определим по закону Ома

\(~R = \frac{\Delta \varphi}{I} = \frac{\rho}{4 \pi} \left ( \frac{1}{r_1} - \frac{1}{r_2} \right ) = \frac{\rho(r_2 - r_1)}{4 \pi r_2 r_1}\) . (4)

Как и следовало ожидать, полученное значение сопротивления не зависит от «придуманного» заряда внутренней сферы.

Итак, суть использованного метода сводится к независимому расчету разности потенциалов и силы тока между сферами, при заданном значении заряда сферы. Величина этого заряда сокращается при вычислении сопротивления.

Интересно отметить, что если расстояние между сферами Δr = r₂ - r₁ значительно меньше их радиусов, то в знаменателе формулы (4) можно пренебречь различием в их радиусах, тогда знаменатель упрощается \(~4 \pi r_2 r_1 \approx 4 \pi r^2 = S\) , то есть становится равным площади поверхности сферы. В этом случае полученная формула (4) превращается в банальную \(~R = \rho \frac{l}{S}\) .

Если радиус внешней сферы устремить к бесконечности (\(~r_2 \to \infty, \frac{1}{r_2} \to 0\)), то рассматриваемая система превращается в заряженный шарик, помещенный в бесконечную проводящую среду. В этом случае сопротивление среды от шарика радиуса r до «бесконечности» оказывается равным

\(~R = \frac{\rho}{4 \pi r}\) . (5)

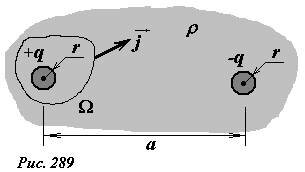
Пример 2. Два одинаковых металлических шарика, радиусы которых равны r, находятся на большом расстоянии a (a >> r) друг от друга в слабопроводящей среде с удельным электрическим сопротивлением ρ (рис. 289). Вычислим электрическое сопротивление среды между шариками.

Для расчета электрического сопротивления мысленно сообщим шарикам электрические заряды, равные по величине и противоположные по знаку (+q,-q). Так расстояние между шариками значительно больше размеров шарика, то можно пренебречь влиянием заряда одного шарика потенциал другого, тогда разность потенциалов между шариками определяется по формуле

\(~\Delta \varphi = \varphi^+ - \varphi^- = \frac{+q}{4 \pi \varepsilon_0 r} - \frac{-q}{4 \pi \varepsilon_0 r} = \frac{q}{2 \pi \varepsilon_0 r}\) , (6)

где φ⁺, φ^- - потенциалы положительно и отрицательно заряженных шариков, соответственно.

Распределение напряженности электрического поля (и соответствующей ему плотности тока) в данном случае достаточно сложной . Однако для вычисления силы тока, стекающего с одного из шариков, знание его не требуется. Мысленно окружим положительно заряженный шарик произвольной замкнутой поверхностью Ω. Поток вектора плотности тока через эту поверхность и будет равен суммарной силе тока между шариками \(~I = \Phi_{\vec j}\) . По закону Ома плотность тока пропорциональна напряженности электрического поля \(~\vec j = \frac{1}{\rho} \vec E\) ; так как поток пропорционален этому вектора, то такое же соотношение будет выполняться и для потоков векторов плотности тока и напряженности поля \(~\Phi_{\vec j} = \frac{1}{\rho} \Phi_{\vec E}\) . Для потока вектора напряженности электрического поля справедлива теорема Гаусса \(~\Phi_{\vec E} = \frac{q}{\varepsilon_0}\) . Таким образом, сила тока между шариками выражается элементарно

\(~I = \Phi_{\vec j} = \frac{1}{\rho} \vec E = \frac{q}{\rho \varepsilon_0}\) . (7)

Теперь легко вычислить искомое сопротивление

\(~R = \frac{\Delta \varphi}{I} = \frac{\rho}{2 \pi r}\) . (8)

Задания для самостоятельной работы.

1. В каком месте при выводе формулы (8) мы учли, что ток идет между шариками?
2. Получите более точную формулу для сопротивления между шариками с учетом расстояния между ними (не полагая его бесконечно большим).

Теперь, внимание! Сравним два результата, формулы (5) и (8) – сопротивления, рассчитанные по этим формулам, отличаются в два раза, хотя, и в одном и другом случае рассматривается стекание тока с металлического шарика в неограниченную среду. Причина такого существенного расхождения заключается в различной структуре поля электрических токов – если в первом случае ток растекается радиально, одинаково во все стороны, то во втором ток преимущественно направлен в одну сторону, ко второму шарику. Тем самым, мы наглядно продемонстрировали, что электрическое сопротивление зависит не только от свойств среды и размеров источника, но и распределением токов.

Примечания

Следующая страница