Слободянюк А.И. Физика 10/14.2

Содержание книги

Предыдующая страница

§14. Движение заряженных частиц в электрическом и магнитном полях

14.2 Плоское движение заряженной частицы в однородном магнитном поле.

При движении заряженной частицы в магнитном поле на нее действует сила Лоренца, которая, как известно, направлена перпендикулярно вектору скорости частицы, поэтому эта сила работы не совершает. Следовательно, при движении частицы в любом стационарном магнитном поле кинетическая энергия и модуль скорости частицы сохраняются – изменяется только направление вектора скорости частицы.

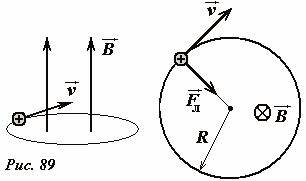
Рассмотрим движение заряженной частицы в однородном магнитном поле, когда вектор скорости частицы направлен перпендикулярно вектору индукции магнитного поля (Рис. 89). Так как модуль скорости частицы сохраняется, сила Лоренца перпендикулярна вектору индукции поля \(~\vec B\), то вектор скорости все время будет перпендикулярен вектору индукции поля. Итак, модули векторов скорости и индукции постоянны, векторы перпендикулярны, следовательно, модуль силы Лоренца также будет оставаться постоянным и равным F_л = qυB. Сила Лоренца является центростремительной, она приводит к искривлению траектории, а, так ее модуль постоянен, то кривизна траектории частицы будет постоянна, то есть траекторией частицы будет окружность. Радиус этой окружности R можно найти на основании уравнения второго закона Ньютона

\(~\frac{m \upsilon^2}{R} = q \upsilon B\) , (1)

из которого находим

\(~R = \frac{m \upsilon}{q B}\) . (2)

Найдем период обращения частицы в магнитном поле

\(~T = \frac{2 \pi R}{\upsilon} = 2 \pi \frac{m}{q B}\) . (3)

Из этой формулы следует интересный и неожиданный вывод – период вращения частицы в магнитном поле не зависит от ее скорости. Частота вращения выражается формулой

\(~\nu = \frac{1}{T} = \frac{1}{2 \pi} \frac{q}{m} B\) , (4)

и называется циклотронной частотой.

14.2.1 Циклотрон.

Постоянство частоты вращения частиц в магнитном поле используется в циклотроне одном из типов ускорителей заряженных частиц – ионов.

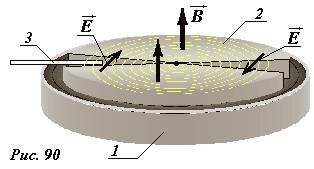
Принципиальная схема ускорителя показана на рис. 90. Основная часть циклотрона – большой электромагнит 1 диаметром в несколько метров и весом в десятки и сотни тонн, между полюсами которого (верхняя часть электромагнита, второй его полюс, на рисунке не показана) находится вакуумная камера. Индукция магнитного поля, создаваемого в камере составляет 1-2 Тл. В вакуумной камере расположены ускоряющие электроды (дуанты) 2. Источник частиц 3 впрыскивает ионы внутрь камеры вблизи ее центра. Под действием постоянного магнитного поля ионы движутся по дугам окружностей. В зазоре электродов создается высокочастотное электрическое поле, частота которого в два раза превышает частоту вращения ионов, которая определяется формулой (4). Ускоряющая разность потенциалов между электродами обычно составляет несколько десятков киловольт. Благодаря этому полю ионы, каждый раз проходя область в зазоре электродов-дуантов, ускоряются, поэтому радиус их орбиты возрастает (см. формулу (2)), а период вращения остается постоянным. Достигая периферийной области, ускоренные ионы выводятся из ускорителя и направляются на мишень и регистрирующие устройства.

Ускорители подобного типа были разработаны и построены в 30-х годах ХХ века и сыграли (и продолжают играть) большую роль в развитии ядерной физики. Не смотря на простоту основных принципов работы ускорителя, циклотрон является очень сложным инженерным сооружением, включающим (помимо описанных элементов) источники питания (электромагнитов, источников частиц, ускоряющей системы, системы регистрации и д.р.), вакуумную систему, блоки управления и регистрации и т.д.

14.2.2 Масс-спектроскопия.

Характеристики движения частиц в магнитном поле (радиус траектории, время движения) зависят от их масс и зарядов. Изучение движения частиц в магнитных полях является основой масс-спектроскопии – метода исследования вещества по спектру масс атомов и молекул, входящих в его состав. Сущность метода состоит в том, что ионизованные атомы и молекулы, проходя через магнитное поле, пространственно разделяются и регистрируются в различных точках. Первоначальными задачами масс-спектроскопии были исследование изотопного состава элементов и прецизионное (точное) измерение масс атомов. В дальнейшем масс-спектроскопия выросла в универсальный аналитический метод, применяющийся в экспериментальной физике, химии, биологии, геологии, технике. Приборы, позволяющие разделять и регистрировать частицы, называются масс-спектрометрами.

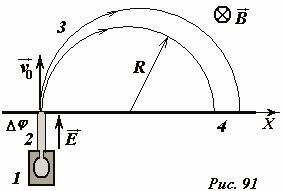
Принцип действия масс-спектрометра показан на рис. 91. Исследуемый образец специальными методами (испарением, электронным ударом) переводится в газообразное состояние, затем образовавшийся газ ионизируется в источнике 1. Затем ионы ускоряются электрическим полем и формируются в узкий пучок в ускоряющем устройстве 2 и через узкую входную щель 3 попадают в камеру 4, в которой создано однородное поперечное магнитное поле. В камере ионы движутся по дуге окружности и попадают на экран 5, где регистрируется место их попадания. Методы регистрации могут быть различными – фотографические, электронные и т.д. Радиус траектории зависит от массы и заряда иона, поэтому разные ионы попадают на экран на различном расстоянии от источника, что и позволяет их разделять и анализировать состав образца.

Найдем координату точки попадания иона на экран в зависимости от его массы, заряда и параметров прибора. В ускоряющем устройстве, пройдя разность потенциалов Δϕ, приобретают скорость υ₀, которая может быть найдена из уравнения закона сохранения энергии

\(~\frac{m \upsilon^2_0}{2} = q \Delta \varphi\) , (1)

из которого следует

\(~\upsilon_0 = \sqrt{2 \frac{q}{m}\Delta \varphi}\) . (2)

Начальной скоростью ионов можно пренебречь, так как обычно она значительно меньше скорости после ускорения. Кроме того, в некоторых приборах применяют дополнительные устройства для выделения частиц имеющих близкие значения скоростей. В магнитном поле ионы движутся по окружности радиуса

\(~R = \frac{m \upsilon_0}{q B} = \frac{m}{q B} \sqrt{2 \frac{q}{m}\Delta \varphi} = \sqrt{\frac{2 \Delta \varphi}{B^2} \frac{m}{q}}\) , (3)

которая зависит от отношения массы к заряду частицы. Координата попадания иона на экран равна диаметру окружности

\(~x_0 = 2R = 2 \sqrt{\frac{2 \Delta \varphi}{B^2} \frac{m}{q}}\) . (4)

В большинстве случаев ионы являются однозарядными (т.е. атомы и молекулы в процессе ионизации теряют один электрон), поэтому фактически прибор разделяет ионы по их массе, формируя масс-спектр исследуемого образца. Если в исходном образце присутствуют различные ионы, то на экране образуется несколько полос, координаты которых позволяют определить состав исходной смеси. Одной из важнейших характеристик масс-спектрометров является их разрешающая способность – характеристика, указывающая, при какой минимальной разности масс, ионы могут различены. Разрешающая способность прибора ограничена, так как полосы на экране не являются абсолютно тонкими, они всегда несколько размыты, имеют некоторую ширину. Если разность координат полос, соответствующих ионам мало различающихся масс (например изотопам одного химического элемента), оказывается меньше ширины полос, то эти полосы сольются, что сделает невозможным разделение (разрешение) двух типов ионов. Кроме того, ширина образующейся полосы Δx определяет погрешность определения массы иона.

Из формулы (4) следует, что масса иона рассчитывается по формуле

\(~m = \frac{q B^2}{8 \Delta \varphi} x^2_0\) . (5)

Если считать, что основную погрешность в определение массы вносит погрешность определения координаты полосы (то есть ее ширина) Δx, то погрешность определения массы следует рассчитывать по формуле

\(~\Delta m = 2 \frac{q B^2}{8 \Delta \varphi} x_0 \Delta x\) ,

а относительная погрешность равна

\(~\varepsilon_m = \frac{\Delta m}{m} = 2 \frac{\Delta x}{x}\) . (6)

Таким образом, уменьшение ширины образующейся полосы является одной из важнейших задач разработчиков масс-спектрометров.

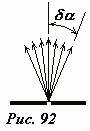
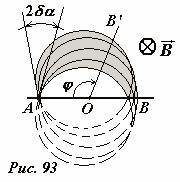
К уширению полосы приводит целый ряд факторов (например, различие в начальных скоростях ионов, ширина входной щели), но одной из основных причин является различия в направлении вектора начальной скорости. Реально, ионы влетают в камеру не строго перпендикулярно экрану, а в пределах некоторого (пусть и небольшого) угла 2δα (рис. 92). Поэтому в масс-спектрометрах применяются специальные системы фокусировки частиц, предназначенные для того, чтобы частицы, вылетевшие из одной точки под разными углами, собирались (фокусировались) в некоторой малой области (в идеале - в точке).

Не случайно в рассматриваемом приборе ионы пролетают половину окружности (их угол поворота равен π) – в этом случае однородное поперечное поле частично фокусирует ионы на регистрирующем экране. Рис. 93 иллюстрирует фокусировку пучка частиц в однородном поперечном магнитном поле. В идеальном случае, когда все частицы вылетают строго в одном направлении, нет необходимости заставлять ионы пролетать половину окружности. В принципе, экран OB’ можно расположить под произвольным углом ϕ. Однако, если ионы вылетают из щели A в пределах некоторого угла 2δα, то пучок ионов (на рис. 93 заштрихован) обладает некоторой шириной, причем его ширина минимальна именно при угле поворота ионов равному π. Найдем эту минимальную ширину пучка, которая равна ширине полосы на экране AB.

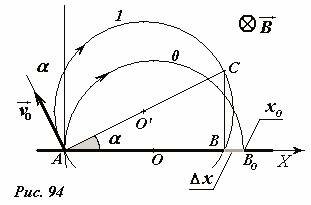
Пусть ион влетает в область магнитного поля под углом α к нормали (Рис. 94) и затем движется по дуге окружности ACB. Для сравнения на рисунке изображена «идеальная» траектория AB₀ частицы, влетевшей перпендикулярно экрану. Если вектор начальной скорости частицы \(~\vec \upsilon_0\) повернут на угол α, то на такой же угол относительно точки вылета повернута и вся траектория, в том числе и ее диаметр AO’C. Ион попадает на экран в точке B, причем угол ∠ABC - прямой, так как он вписан в окружность и опирается на диаметр. Следовательно, координата точки падения B равна

\(~x = 2R \cos \alpha\) . (7)

Эта координата максимальна для «идеальной» траектории α = 0 и уменьшается при увеличении угла отклонения вектора начальной скорости, причем не зависимо от того в какую сторону. Если максимальный угол отклонения равен δα, то ширина полосы равна

\(~\Delta x = 2R (1 - \cos \delta \alpha)\) , (8)

при малом δα следует воспользоваться приближенной формулой \(~\cos \delta \alpha \approx 1 - \frac{(\delta \alpha)^2}{2}\), и рассчитать ширину полосы по формуле

\(~\Delta x = 2R (1 - \cos \delta \alpha) \approx R (\delta \alpha)^2\) , (9)

а относительное уширение полосы оказывается равным

\(~\frac{\Delta x}{x_0} = \frac{\Delta x}{2 R} = \frac{1}{2} (\delta \alpha)^2\) . (10)

Как следует из полученного результата, уширение полосы является малой величиной более высокой степени (действительно (δα)² < δα при δα < 1), что и свидетельствует об эффекте фокусировки.

В настоящее время разработаны многочисленные типы масс-спектрометров, принципы работы которых отличаются от рассмотренных выше: с другими методами фокусировки частиц, с иной конфигурацией магнитного поля. Изготавливаются также динамические масс-спектрометры, в которых массы исследуемых ионов определяются по времени пролета от источника до регистрирующего устройства.

14.2.3 Магнитная отклоняющая система.

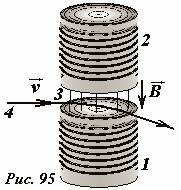
Магнитное поле также используется для отклонения пучков частиц. Причем магнитные отклоняющие системы электронных пучков в телевизионных трубках (кинескопах) и осциллографах используются гораздо чаще электростатических. Магнитная отклоняющая система проста – состоит из двух электромагнитов 1-2, в зазоре 3 которых проходит электронный пучок 4 (Рис. 95).

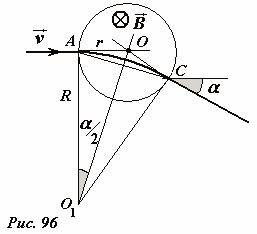
Найдем угол отклонения электронного луча в этом случае. Пусть область, занятая однородным магнитным полем индукции \(~\vec B\) (зазор между торцами магнитов, магнитным полем вне этой области можно пренебречь) имеет форму цилиндра радиуса r (Рис. 96). Для простоты будем считать, что пучок электронов движется по направлению к центру этой области и попадает в нее в точке A. Под действием магнитного поля пучок отклоняется и движется по дуге окружности AC, радиус которой равен

\(~R = \frac{m \upsilon}{eB}\) . (1)

угол отклонения луча α легко находится из рисунка. Из прямоугольного треугольника AOO₁ следует, что

\(~\operatorname{tg} \frac{\alpha}{2} = \frac{r}{R} = \frac{er}{m \upsilon} B\) , (2)

или

\(~\alpha = 2 \operatorname{arctg} \left ( \frac{er}{m \upsilon} B \right )\) . (3)

При малых углах (когда тангенс приблизительно равен самому углу) отклонение пропорционально индукции поля, которая в свою очередь пропорциональна силе тока электромагнита. Изменяя величину этого тока можно регулировать направление пучка электронов.

Примечания

Следующая страница