Слободянюк А.И. Физика 10/19.4.III

Содержание книги

Предыдующая страница

§19. Волновые процессы

19.4 Интерференция волн.

19.4.3 Интерференция двух плоских волн.

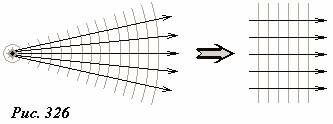
Участок сферической волны на большом расстоянии от источника можно приближенно рассматривать как плоскую волну. Поэтому использованное нами приближение «параллельных лучей» равносильно переходу к рассмотрению плоских волн – действительно, если семейство волновых лучей является набором параллельных прямых, то перпендикулярные им волновые поверхности представляют набор параллельных плоскостей (рис. 326).

Следовательно, интерференция сферических волн на большом расстоянии от источников может быть описана как интерференция более простых плоских волн.

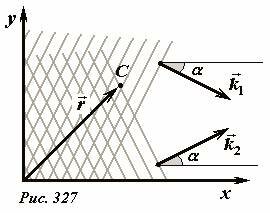
Пусть в некоторой области пространства распространяются две плоские монохроматические волны одинаковых частот. Построим декартовую систему координат так, чтобы ее плоскость xOy была перпендикулярна волновым поверхностям обеих волн, а направления распространения волн были симметричны относительно оси Ox (рис. 327). При этом волновые векторы волн образуют равные углы α с этой осью.

Уравнение плоской волны имеет вид

\(~u(\vec r,t) = a \cos (\omega t - \vec k \cdot \vec r)\) , (1)

где \(~\vec k\) - постоянный волновой вектор волны, \(~\vec r\) - радиус-вектор точки, в которой задано возмущение \(~u(\vec r,t)\).

Обратите внимание, на отличие функции (1) от уравнения сферической волны, в котором вместо скалярного произведения \(~(\vec k \cdot \vec r)\) стоит произведение волнового числа k (а не вектора!) на расстояние до точки наблюдения r (а не радиус-вектор этой точки!)

Используя принцип суперпозиции, запишем суммарное возмущение, вызванное обеими волнами в произвольной точке, и преобразуем его к виду:

\(~U(\vec r,t) = a \cos (\omega t - \vec k_1 \cdot \vec r) + a \cos (\omega t - \vec k_2 \cdot \vec r) = 2 a \cos \left(\omega t - \frac{(\vec k_1 + \vec k_2) \cdot \vec r}{2} \right) \cos \left(\frac{(\vec k_1 - \vec k_2) \cdot \vec r}{2} \right)\) . (2)

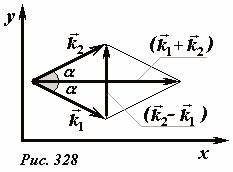
Описанный выбор системы координат позволяет записать сумму и разность волновых векторов в очень простом виде (Рис. 328). Вектор суммы этих векторов направлен параллельно оси Ox, его модуль равен

\(~|\vec k_1 + \vec k_2| = 2k \cos \alpha\) . (3)

Вектор разности волновых векторов направлен параллельно оси Oy, его модуль равен

\(~|\vec k_1 - \vec k_2| = 2k \sin \alpha\) . (4)

С учетом этих выражений уравнение результирующей волны (2) записывается в виде

\(~\begin{matrix} U(\vec r,t) = 2 a \cos \left(\omega t - \frac{(\vec k_1 + \vec k_2) \cdot \vec r}{2} \right) \cos \left(\frac{(\vec k_1 - \vec k_2) \cdot \vec r}{2} \right) = 2 a \cos (\omega t - kx \cos \alpha) \cos (ky \sin \alpha) = \\ = (2a \cos (ky \sin \alpha)) \cos (\omega t - kx \cos \alpha) = A(y) \cos (\omega t - \Phi(x)) \end{matrix}\) . (5)

В преобразованиях учтено, что проекция радиус-вектора точки на ось Ox равна координате x этой точки, аналогично, проекция радиус-вектора на ось Oy есть координата y.

Из формулы (5) следует, фаза результирующей волны

\(~\Phi(x) = kx \cos \alpha\) (6)

зависит только координаты x, следовательно, поверхности постоянной фазы (волновые поверхности) являются плоскостями перпендикулярными оси Ox. В свою очередь, амплитуда волны

\(~A(y) = 2a \cos (ky \sin \alpha)\) (7)

не постоянна, но зависит только от координаты y.

Таким образом, результирующую волну можно представить как плоскую волну, распространяющуюся вдоль оси Ox, амплитуда которой модулирована – изменяется при изменении координаты y.

На рис. 329 показан трехмерный график зависимости амплитуды волны от координат, а на рис. 330 профиль этой плоской волны в некоторый момент времени. В таком представлении волновой вектор суммарной волны равен полусумме волновых векторов \(~\frac{(\vec k_1 + \vec k_2) \cdot \vec r}{2}\). Поэтому длина волны, распространяющейся вдоль оси Ox равна

\(~\lambda' = \frac{2 \pi}{k'} = \frac{2 \pi}{k \cos \alpha} = \frac{\lambda}{\cos \alpha}\) , (8)

что больше длины волны исходных плоских волн.

Найдем также ширину интерференционной полосы, под которой будем понимать расстояние Δy между двумя прямыми, на которых амплитуда волны максимальна, или, что равносильно, расстояние между двумя минимумами. Из выражения (7) для амплитуды волны следует, что координаты y₀ ближайших к оси Ox линий минимума амплитуды удовлетворяют уравнению

\(~ky \sin \alpha = \frac{2 \pi}{\lambda} y_0 \sin \alpha = \pm \frac{\pi}{2}\) . (9)

Из этого уравнения следует, что ширина полосы равна

\(~\Delta y = 2 y_0 = \frac{\lambda}{2 \sin \alpha}\) . (10)

Если угол схождения волн (т.е. угол между их угловыми векторами) ψ = 2α является малым, то ширина полосы оказывается равной отношению длины волны к углу схождения волн:

\(~\Delta y_0 = \frac{\lambda}{2 \sin \alpha} \approx \frac{\lambda}{2 \alpha} = \frac{\lambda}{\psi}\) . (11)

В этом же приближении cos α ≈ 1, поэтому длину результирующей волны можно считать равной длине исходных волн.

Из полученных соотношений также следует очевидный результат, если направления распространения исходных волн совпадают, то результирующая волна является такой же плоской волной удвоенной амплитуды.

19.4.4 Стоячие волны.

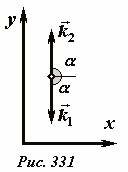
При описании интерференции двух плоских волн мы сознательно опустили очень интересный частный случай – когда две одинаковых волны распространяются на встречу друг другу. Для того, чтобы рассмотреть его необходимо в общей формуле (5) из предыдущего раздела следует просто положить угол \(~\alpha = \frac{\pi}{2}\) (Рис. 331). В этом случае волновые векторы встречных волн противоположны, поэтому обозначим \(~\vec k_1 = -\vec k_2 = \vec k\). Тогда результирующая волна описывается выражением (при сохранении прежней ориентации осей координат):

\(~U(\vec r,t) = 2 a \cos (\omega t) \cos (\vec k \cdot \vec r) = 2 a \cos (\omega t) \cos (ky)\) . (1)

В полученном выражении пространственная и временная зависимости «разделись», то есть волна в обычном понимании, как «нечто, распространяющееся в пространстве», исчезла. Действительно, формулу (1) описывает колебания всех точек среды, происходящие в одной фазе, но амплитуда этих колебаний зависит от координаты. Чтобы сделать это утверждение более явным, переставим сомножитель в формуле (1):

\(~U(y,t) = (2a \cos (ky)) \cdot \cos (\omega t) = A(y) \cos (\omega t)\) . (2)

где зависимость амплитуды от координаты имеет вид \(A(y)= 2a \cos(ky)\).

Колебания среды, при которых все точки колеблются в одной фазе, но с разными амплитудами называются стоячими волнами.

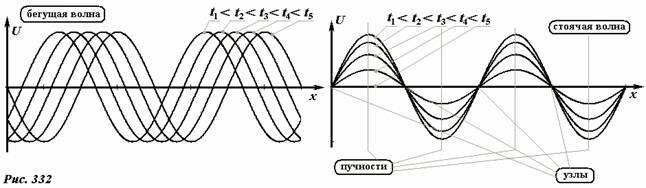
Рис. 332 демонстрирует различие между стоячей и «обычной» бегущей волной (в обоих случаях показаны профили волн в последовательные моменты времени). В первой одинаковы фазы колебаний, но различны амплитуды; во второй – постоянны амплитуды, но различны фазы колебаний, что и приводит к перемещению максимумов и минимумов возмущений в пространстве.

В стоячей волне существую точки, амплитуда колебаний которых равна нулю, они называются узлами волны. Точки, амплитуда колебаний которых максимальна, называются пучностями волны. Иногда расстояние между двумя соседними узлами (или соседними пучностями) называют длиной стоячей волны. При таком определении длина стоячей волны оказывается в два раза меньше длины бегущей волны.

Стоячие волны можно рассматривать как собственные колебания ограниченных тел, так как в этом случае все точки тела колеблются синфазно. Для примера, рассмотрим еще раз колебания упругой цепочки (19.2 Рис. 292). Движение шариков этой цепочки по-прежнему описываются системой уравнений

\(~a_n = -\omega^2_0 u_n + \frac{\omega^2_0}{2} u_{n-1} + \frac{\omega^2_0}{2} u_{n+1}\) , (3)

где - частота колебаний одного шарика, при условии, что два его соседних шарика закреплены (напомним, что эта система уравнений справедлива как для продельных, так и поперечных волн – различия между ними заключается в различных способах определения параметра ω₀). Ограничим цепочку, считая, что шарики под номерами n = 0 и n = N +1 закреплены, поэтому для них смещения всегда равны нулю

\(~u_0(t) = 0, u_{N+1}(t) = 0\) . (4)

Эти дополнительные условия, накладываемые на систему уравнений, называются граничными условиями.

Рассматриваемая ограниченная цепочка обладает N степенями свободы, поэтому следует ожидать, что число ее собственных частот колебаний также равно N.

Теперь решение уравнений (3) необходимо искать в форме стоячей волны, для которой частоты и фазы колебаний для всех шариков одинаковы, а амплитуды изменяются по гармоническому закону. Попытаемся найти решение системы уравнений

\(~u_n = A \sin n \beta \cdot \cos \omega t\) . (5)

При такой записи при n = 0 колебания нулевого шарика отсутствуют. Также должно выполняться второе граничное условие \(u_{N+1}(t) = 0\), которое налагает ограничения на возможные значения параметра β. Это условие должно выполняться в любой момент времени, что возможно только при

\(~\sin (N + 1) \beta = 0\) , (6)

откуда следует \((N + 1) \beta_j = j \pi\), или

\(~\beta_j = j \frac{\pi}{N + 1} ; j = \pm 1, \pm 2 \ldots \pm N\) . (7)

При j = N + 1 все функции, описываемые выражением (5) обращаются в нуль, а j > N наборы этих функций, начинают повторяться, поэтому мы ограничили значения индекса j. Подставим пробное решение (5) с определенным значением β_j в уравнения движения (3):

\(~-A \omega^2 \sin n \beta_j \cos \omega t = -A \omega^2_0 \sin n \beta_j \cos \omega t + A \frac{\omega^2_0}{2} \sin (n-1) \beta_j \cos \omega t + \frac{\omega^2_0}{2} \sin (n+1) \beta_j \cos \omega t\) ,

после сокращения и применения формулы для суммы синусов получим

\(~-\omega^2 \sin n \beta_j = -\omega^2_0 \sin n \beta_j + \omega^2_0 \sin n \beta_j \cos \beta_j\) .

Из этого равенства с учетом выражения (7), определяем набор частот колебаний, при которых возможно существование стоячих волн на ограниченной цепочке:

\(~\omega_j = \omega_0 \sqrt{1 - \cos \frac{j \pi}{N + 1}} ; j = 1,2,3 \ldots N\) . (8)

Отметим, что при j = N + 2 соответствующая собственная частота равна

\(~\omega_{N+2} = \omega_0 \sqrt{1 - \cos \frac{(N + 2) \pi}{N + 1}} = \omega_0 \sqrt{1 - \cos \left(2 \pi - \frac{N \pi}{N + 1} \right)} = \omega_N\) ,

что совпадает с частотой ω_N. Аналогично при больших значениях j частоты повторяются, поэтому действительно число различных частот равно N. Формула (8) также приводит к заранее очевидному результату для цепочки из трех шариков, два крайних из которых закреплены, в этом случае (N = 1) существует единственная собственная частота \(~\omega_1 = \omega_0 \sqrt{1 - \cos \frac{\pi}{2}} = \omega_0\), соответствующая смыслу параметра ω₀.

Таким образом, мы показали, что на ограниченной упругой цепочке могут существовать стоячие волны, число типов которых совпадает с числом степеней свободы. Граничные условия (4) приводят к тому, что частоты этих волн принимают строго определенный дискретный набор значений. Полученным частотам и соответствующим им типам стоячих волн может быть придан иной, геометрический смысл.

Движения шариков в стоячей волне описываются функциями (5), которые при возможных значениях параметра β_j имеют вид (второй индекс указывает тип возможной стоячей волны)

\(~u_{n,j}(t) = A \sin n \frac{j \pi}{N+1} \cdot \cos \omega t\) . (9)

Перейдем в этой формуле от номера шарика к его координате \(x_n = nl\) (где l - расстояние между центрами шариков), тогда величина \((N +1)l = L\) равна длине цепочки. Тогда набор функций (9) можно приближенно заметить одной функцией двух переменных \(u_{n,j}(t) \to u_j (x,t)\), причем

\(~u_j (x,t) = A \sin nl \frac{j \pi}{(N+1)l} \cdot \cos \omega t = A \sin j \pi \frac{x}{L} \cdot \cos \omega t\) . (10)

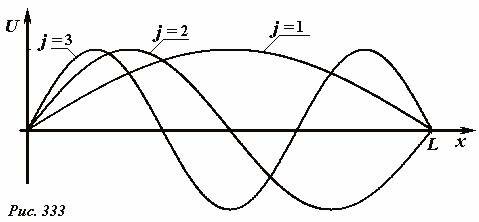
Эта формула позволяет найти длину соответствующей стоячей волны. Нулевой шарик в цепочке покоится, то есть, расположен в узле стоячей волны. Координата следующего узла удовлетворяет условию \(~j \pi \frac{x_1}{L} = \pi\), из которого следует, что \(~x_1 = \frac{L}{j}\). Эта величина равна длине стоячей волны (или половине длины бегущей волны)\[~x_1 = \lambda_c = \frac{\lambda}{2}\]. Таким образом, индекс j равен числу длин стоячих волн, укладывающихся на длине цепочки, или, что равносильно, – числу пучностей в стоячей волне. На рис. 333 показаны профили стоячих волн, соответствующих различным значениям этого параметра.

С помощью такого подхода частоты собственных колебаний могут быть определены с помощь формулы, связывающей частоту, длину волны и скорость ее распространения λν = с, из которой следует, что

\(~\omega_j = 2 \pi \nu_j = 2 \pi \frac{c}{\lambda_j} = \pi \frac{c}{L} j\) , (11)

здесь λ_j - длина бегущей волны, которая в соответствии с проведенными рассуждениями в два раза больше длины стоячей волны, поэтому \(~\lambda_j = \frac{L}{j}\).

В общем случае скорость распространения волны зависит от ее частоты (дисперсии), поэтому выражение (11) следует рассматривать как уравнение, в котором неизвестная частота входит явно в левую часть, и как аргумент зависимости с(ω). В том же случае, когда скорость волны постоянна, не зависит от частоты, то формула (11) определяет собственные частоты колебаний струны с закрепленными концами.

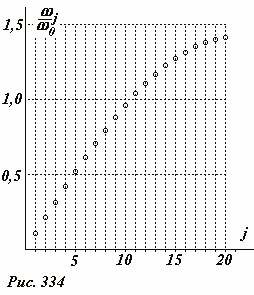
На рис. 334 представлен набор (спектр) рассчитанных по формуле (8) собственных частот упругой цепочки, содержащей N = 20 колеблющихся шариков. Обратите внимание, низшие частоты практически эквидистантны (отличаются на одну и ту же величину), с ростом частот ее зависимость от порядкового номера становится нелинейной – начинает сказываться зависимость скорости волны от частоты.

Еще раз обратим внимание на неоднозначность решения системы уравнений (3): сначала мы искали (и нашли!) решение в виде бегущих волн; а затем в виде стоячих. Правда, во втором случае мы наложили дополнительные (граничные) условия. В общем случае, для того, чтобы решение системы было однозначным необходимо задать еще и начальные условия: значения начальных положение и скоростей всех шариков цепочки. Тогда решение может быть представлено в виде суперпозиции найденных волн (построение решения в виде суммы найденных решений допустимо, так как сама система является линейной): для бесконечной струны в виде суперпозиции бегущих волн произвольных частот; для струны с закрепленными концами – в виде суперпозиции стоячих волн с дискретным набором собственных частот.

Стоячие волны могут существовать не только в одномерных системах тапа рассмотренной цепочки, или натянутой струны. На любой упругой пластине конечных размеров при определенных условиях возникают стоячие волны, то есть такие колебания, при которых все точки колеблются с одной частотой и в одной фазой. Так же как и в одномерном случае точки, амплитуда колебаний которых равна нулю, называются узлами. Эти точки образуют непрерывные линии на поверхности пластины, называемые узловыми линиями. Некоторые точки пластины могут быть закреплены, в этом случае они также являются узловыми. Точки, амплитуды колебаний которых максимальны, называются пучностями. Типы возможных стоячих волн пластинки зависят от ее формы. Кроме того, формы стоячих волн зависят от граничных условий: края пластинки могут быть закреплены, могут быть свободны. В первом случае на границе будут располагаться узлы стоячей волны, во втором – пучности. Частоты этих собственных колебаний (т.е. стоячих волн) зависят не только от размеров, формы пластины, граничных условий, но также от скорости распространения волн по пластине.

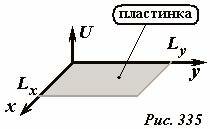
Наиболее просто описываются стоячие волны на прямоугольной пластинке с закрепленными краями. Если задать декартовую систему координат, так чтобы ее оси совпадали с краями пластинки (Рис. 335), то функции, описывающие колебания пластинки имеют вид

\(~U (x,y,t) = A \sin (k_x x) \sin (k_y y) \cos \omega t\) , (12)

где k_x, k_y - волновые числа, значения которых определяются граничными условиями. Так как края пластинки закреплены, то ее возмущения должны обращаться в нуль: при x = 0, что выполняется автоматически для функций вида (12); и при x = L_x (L_x - длина стороны пластинки, направленной вдоль оси Ox). Второе условие накладывает ограничения на возможные значения параметра k_x, так как для его удовлетворения следует положить

\(~k_x L_x = j_x \pi, j_x = \pm 1, \pm 2, \pm 3 \ldots\) . (13)

Следовательно, волновое число k_x может принимать значения

\(~k_x = j_x \frac{\pi}{L_x}\) . (14)

Аналогичные рассуждения приводят к следующим значениям волнового числа k_y

\(~k_y = j_y \frac{\pi}{L_y}\) , (15)

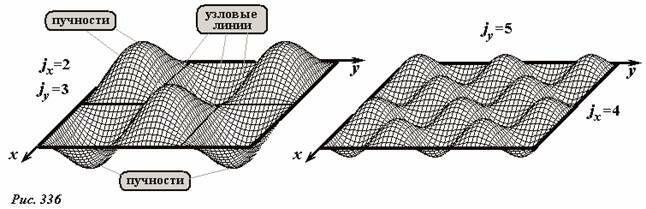
где L_y - длина стороны пластинки, направленной вдоль оси Oy. Таким образом, форма собственных колебаний пластинки определяется двумя целыми числами j_x, j_y - каждое из которых равно числу пучностей волны вдоль соответствующих сторон пластинки. На рис. 336 показаны два типа стоячей волны на прямоугольной пластинке с различными значениями этих параметров.

Возможный набор частот собственных колебаний такой пластинки также зависит от этих двух целочисленных параметров, причем они равны

\(~\omega = c \sqrt{k^2_x + k^2_y} = c \sqrt{\left(j_x \frac{\pi}{L_x} \right)^2 + \left(j_y \frac{\pi}{L_y} \right)^2}\) , (16)

где с - скорость распространения волн по пластинке.

Данная формула приведена без доказательств. Однако убедится в ее справедливости можно следующим образом. В свое время в разделе 19.2.4 мы записали волновое уравнение, описывающие колебания одномерной струны. Это уравнение очевидным образом обобщается на двумерный случай колебаний плоской пластинки

\(~\frac{\partial^2 u}{\partial t^2} = c^2 \left(\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} \right)\) .

Подставьте в это уравнение функцию (12) и убедитесь, что она удовлетворяет ему только при выполнении формулы (16).

На рис.336 показаны формы колебаний пластинок в определенный момент времени. С течением времени их форма не изменяется – периодически изменяется только величина отклонения от положения равновесия. На рис. 337 показаны профили колеблющейся пластинки в последовательные моменты времени через одну восьмую периода колебаний – всего половина периода. За этот промежуток времени на месте возвышения образуется впадина и наоборот.

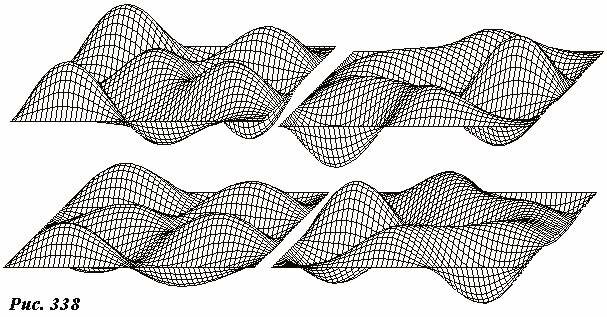
Реальные колебания такой пластинки могут иметь более сложную форму, но любая из них представима в виде суперпозиции собственных колебаний, описываемых функциями (12). Отметим, что, так как собственные колебания имеют различные частоты, то при их суперпозиции профиль пластинки изменяется более сложным образом, чем простое изменение величины отклонения. Рис. 338 иллюстрирует это утверждение. На нем показаны профили пластики, колебание которой является суммой всего двух собственных колебаний.

Виды собственных поперечных колебаний пластинок различных форм легко наблюдать и изучать с помощью простого эксперимента. Исследуемую пластинку располагают горизонтально, закрепляют в нужных местах и посыпают тонким слоем мелкозернистого песка. После чего возбуждают ее колебания. Проще всего это сделать, если провести по ее незакрепленному краю смычком. В ходе колебаний песок, находящийся в местах пучностей приходит в движение и скапливается в тех точках пластинки, которые неподвижны, то есть на узловых линиях. В результате на пластинке образуется хорошо видимая сетка узловых линий, «нарисованная» крупицами песка. Образованные таким способом узоры получили название фигур Хладни, по имени ученого впервые предложивший способ из получения.

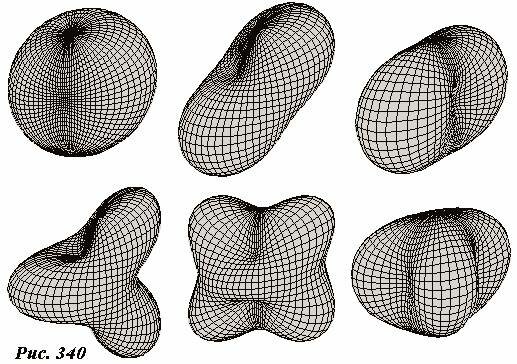
Собственными колебаниями обладают также двумерные поверхности, отличные от плоских. Так на рис. 340 показаны некоторые виды собственных колебаний сферы. Для большего зрительного эффекта амплитуда этих колебаний сильно преувеличена. Эти собственные колебания описываются более сложными функциями, чем (12). Однако вид этих колебаний (и их частоты) также определяется двумя целыми числами. Так для сферы они определяют число пучностей «вдоль параллелей и меридианов». Так на длине экватора должно укладываться целое число длин стоячих волн.

Собственными колебаниями обладают и трехмерные тела. Формы этих колебаний могут быть весьма причудливы - они зависят от формы тела, граничных условий, точек закрепления. Важно отметить, что собственные колебания трехмерных тел определяются тремя целочисленными параметрами. Так в простейшем случае упругих колебаний сплошного параллелепипеда со сторонами L_x, L_y, L_z и жестко закрепленными гранями, его собственные колебания описываются функциями, аналогичными (12):

\(~U (x,y,z,t) = A \sin \left(j_x \pi \frac{x}{L_x} \right) \sin \left(j_y \pi \frac{y}{L_y} \right) \sin \left(j_z \pi \frac{z}{L_z} \right) \cos \omega t\) . (17)

Частоты этих колебаний также зависят от скорости распространения волн и определяются набором трех целых чисел j_x, j_y, j_z:

\(~\omega = c \sqrt{\left(j_x \frac{\pi}{L_x} \right)^2 + \left(j_y \frac{\pi}{L_y} \right)^2 + \left(j_z \frac{\pi}{L_z} \right)^2}\) . (18)

Для тел другой формы типы собственных колебаний и их частоты описываются гораздо более сложными функциями, однако, в любом случае они определяются тремя целыми параметрами.

Большое значение имеют собственные колебания ограниченных объемов воздуха в различных музыкальных инструментах. Их полости-резонаторы имеют сложную геометрическую форму, поэтому типы возможных стоячих звуковых волн (и их частоты) весьма разнообразны. Чем более совершенный музыкальный инструмент, тем больше собственных частот возбуждается при его звучании, поэтому спектр его звучания оказывается богат различными частотами, поэтому звук имеет богатый тембр.

Еще один пример стоячих волн – формы электронных облаков в атомах, которые вы изучали в курсе химии. Однако эти волны имеют совсем иную физическую природу и еще ни разу не упоминались нами. С ними познакомимся при изучении основ квантовой механики.

Примечания

Следующая страница