Слободянюк А.И. Физика 10/9.11
§9. Электрическое поле и его свойства
9.11 Примеры расчета потенциалов электростатических полей.
Поле равномерно заряженной сферы.
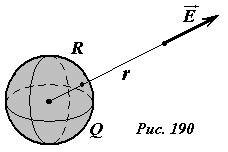
Пусть электрическое поле создается зарядом Q, равномерно распределенным по поверхности сферы радиуса R (Рис. 190). Для вычисления потенциала поля в произвольной точке, находящейся на расстоянии r от центра сферы, необходимо вычислить работу, совершаемую полем при перемещении единичного положительного заряда от данной точки до бесконечности. Ранее мы доказали, что напряженность поля равномерно заряженной сферы вне ее эквивалентно полю точечного заряда, расположенного в центре сферы. Следовательно, вне сферы потенциал поля сферы будет совпадать с потенциалом поля точечного заряда
В частности, на поверхности сферы потенциал равен \(~\varphi_0 = \frac{Q}{4 \pi \varepsilon_0 R}\) . Внутри сферы электростатическое поле отсутствует, поэтому работа по перемещению заряда из произвольной точки, находящейся внутри сферы, на ее поверхность равна нулю A = 0, поэтому и разность потенциалов между этими точками также равна нулю Δφ = -A = 0. Следовательно, все точки внутри сферы имеют один и тот же потенциал, совпадающий с потенциалом ее поверхности \(~\varphi_0 = \frac{Q}{4 \pi \varepsilon_0 R}\) .
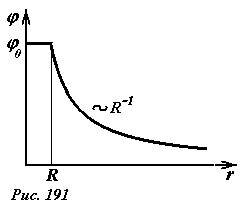
Итак, распределение потенциала поля равномерно заряженной сферы имеет вид (Рис. 191)
Обратите внимание, поле внутри сферы отсутствует, а потенциал отличен от нуля! Этот пример является яркой иллюстрацией, того, что потенциал определяется значением поля от данной точки до бесконечности.
Поле равномерно заряженного кольца.
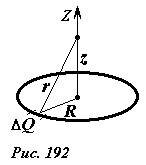
Вычислим потенциал поля, создаваемого зарядом Q, равномерно распределенным по тонкому кольцу радиуса R, причем ограничимся расчетом потенциала поля только на оси кольца (Рис. 192). Ранее мы вычислили напряженность поля на оси кольца, как функцию расстояния до его центра. Поэтому для вычисления потенциала можно, в принципе, подсчитать работу, совершаемую полем при перемещении заряда от данной точки до бесконечности. Однако, в данном случае проще воспользоваться принципом суперпозиции для потенциала поля. Для этого мысленно разобьем кольцо на малые участки, несущие заряд ΔQk. Тогда в точке, находящейся на расстоянии z от его центра, этот заряд создает поле, потенциал которого равен
Так как все точки кольца находятся на одинаковом расстоянии \(~r = \sqrt {R^2 + z^2}\) от рассматриваемой точки, то суммирование потенциалов полей, создаваемых зарядами ΔQk сводится к суммированию самих зарядов
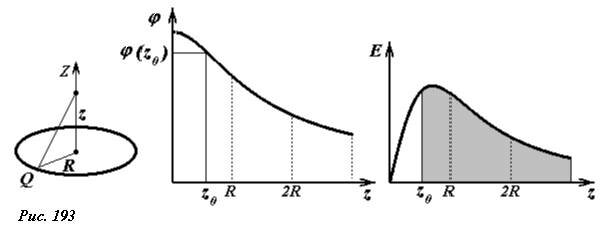
График этой функции показан на рисунке. Там же повторен график зависимости напряженности поля кольца на его оси от расстояния до центра кольца. Напомним, что значения потенциала φ(z0) в точке с координатой z0 численно равно площади под графиком зависимости E(z) в интервале от z0 до \(~z \to \infty\) .
Обратите внимание – так как проекция вектора напряженности не изменяет свой знак, то функция φ(z) является монотонной.
Поле равномерно заряженной бесконечной пластины.
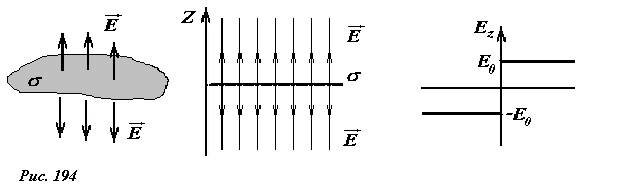
Ранее мы показали, что электрическое поле, создаваемое бесконечной равномерно заряженной пластиной является однородным, то есть напряженность поля одинакова во всех точках, причем вектор напряженности направлен перпендикулярно плоскости, а его модуль равен \(~E_0 = \frac{\sigma}{2 \varepsilon_0}\) . Семейством силовых линий такого поля явяется набор параллельных прямых, перпендикулярных пластине. На рис. 194 так же изображен график зависимости проекции вектора напряженности поля Ex на ось Z перпендикулярную пластине (начало отсчета этой оси расположим на пластине). Понятно, что потенциал данного поля зависит только от координаты z, то есть эквипотенциальные поверхности в данном случае являются плоскостями, параллельными заряженной пластине.
При традиционном выборе нулевого уровня потенциала \(~\varphi(z \to \infty) = 0\) , потенциал произвольной точки равен работе по перемещению единичного положительного заряда из данной точки на бесконечность. Так как модуль напряженности постоянен, то такая работа (а, следовательно, и потенциал) оказывается равной бесконечности! Следовательно, указанный выбор нулевого уровня потенциала в данном случае непригоден.
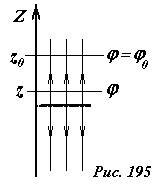
Поэтому следует воспользоваться произволом выбора нулевого уровня. Достаточно выбрать произвольную точку с координатой z = z0, и приписать ей произвольное значение потенциала φ(z0) = φ(0) (Рис. 195). Теперь, чтобы вычислить значение потенциала в произвольной точке φ(z), можно воспользоваться соотношением между напряженностью и потенциалом поля \(~\Delta \varphi = - \vec E \cdot \Delta \vec r\) . Учитывая, что в данном случае напряженность поля постоянна (при z > 0) это выражение записывается в виде
из которого следует искомая зависимость потенциала от координаты (при z > 0)
В частности, можно задать произвольное значение потенциала самой пластины, то есть положить при z = z0 = 0 φ = φ(0). Тогда значение потенциала в произвольной точке определяется функцией
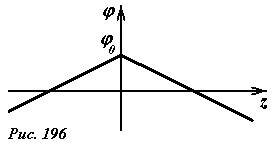
график которой показан на рисунке 196.
То, что потенциал относительно бесконечности оказался бесконечно большим, вполне очевидно – ведь и бесконечная пластина обладает бесконечно большим зарядом. Как мы уже подчеркивали, такая система является идеализацией – бесконечных пластин не существует. В реальности все тела имеют конечные размеры, поэтому для них традиционный выбор нулевого потенциала возможен, правда в этом случае распределение поля может быть очень сложным. В рамках же рассматриваемой идеализации удобнее воспользоваться использованным нами выбором нулевого уровня.
Задание для самостоятельной работы.
-
Покажите, что при произвольном выборе нулевого уровня потенциала функция (4) может быть обобщена на все значения координаты z (в том числе и отрицательные) следующим образом
-
\(~\varphi(z) = \varphi_0 - E_0 (|z| - z_0)\) . - Постройте график этой функции.
-
Поле двух параллельных равномерно заряженных пластин.
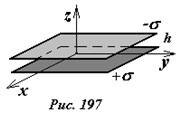
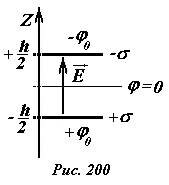
Найдем распределение потенциала поля, создаваемого двумя одинаковыми равномерно заряженными параллельными пластинами, заряды которых равны по модулю и противоположны по знаку [1] (Рис. 197). Обозначим поверхностную плотность заряда на одной пластине +σ, а на другой -σ . Расстояние между пластинами h будем считать значительно меньшим размеров пластин. Введем систему координат, ось z которой перпендикулярна пластинам, начало координат разместим по средине между пластинами. Очевидно, для бесконечно больших пластин все характеристики поля (напряженность и потенциал) зависят только от координаты z. Для расчета напряженности поля в различных точках пространства воспользуемся полученным выражением для напряженности поля, создаваемого бесконечной равномерно заряженной пластиной и принципом суперпозиции.
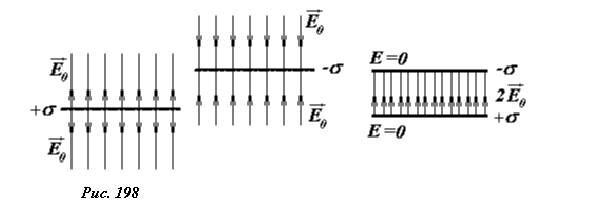
Каждая равномерно заряженная пластина создает однородное поле, модуль напряженности которого равен \(~E_0 = \frac{\sigma}{2 \varepsilon_0}\) , а направления указаны на рисунке 198.
Складывая напряженности полей по принципу суперпозиции, получим, что в пространстве между пластинами напряженность поля \(~E = 2E_0 = \frac{\sigma}{\varepsilon_0}\) вдвое превышает напряженность поля одной пластины (здесь поля отдельных пластин параллельны), а вне пластин поле отсутствует (здесь поля отдельных пластин противоположны).
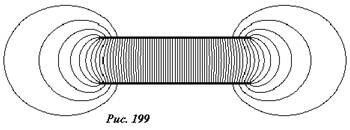
Строго говоря, для пластин конечных размеров поле не является однородным, силовые линии поля пластин конечных размеров показаны на рисунке 199. Наиболее сильные отклонения от однородности наблюдаются вблизи краев пластин (часто эти отклонения называют краевыми эффектами). Однако, в области прилегающей к середине пластин поле с высокой степенью точности можно считать однородным, то есть в этой области можно пренебречь краевыми эффектами. Заметим, что погрешности такого приближения тем меньше, чем меньше отношение расстояния между пластинами к их размерам.
Для однозначного определения распределения потенциала поля, необходимо выбрать уровень нулевого потенциала. Будем считать, что потенциал равным нулю в плоскости расположенной по средине между пластинами, то есть, положим φ = 0 при z = 0.
Не смотря на произвол в выборе нулевого уровня потенциала, наш выбор может быть логически обоснован на основании симметрии системы. Действительно, рассматриваемая система зарядов зеркально повторяет себя при зеркальном отражении относительно плоскости z = 0 и одновременном изменении знаков зарядов. Поэтому желательно, чтобы и распределение потенциала обладало такой же симметрией: восстанавливалось при зеркальном отражении с одновременным изменением знака всех функций поля. Выбранный нами способ выбора нулевого потенциала удовлетворяет такой симметрии.
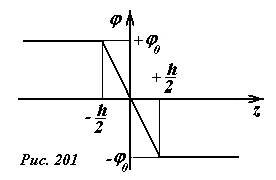
Обозначим потенциал положительно заряженной пластины +φ0, тогда потенциал отрицательно заряженной пластины будет равен -φ0. Эти потенциалы легко определить, используя найденное значение напряженности поля между пластинами и связь между напряженностью и разностью потенциалов электрического поля. Уравнение этой связи в данном случае имеет вид φ0 - (-φ0) = Eh. Из этого соотношения определяем значения потенциалов пластин \(~\varphi_0 = \frac{\sigma h}{2 \varepsilon_0}\) . Учитывая, что между пластинами поле однородное (поэтому потенциал изменяется линейно), а вне пластин поле отсутствует (поэтому здесь потенциал постоянен), зависимость потенциала от координаты z имеет вид (рис. 201)
Задания для самостоятельной работы.
- Во всех рассмотренных примерах проделайте обратную операцию: по найденному распределению потенциала с помощью формулы \(~E_x = -\frac{\Delta \varphi}{\Delta x}\) рассчитайте напряженности рассмотренных полей.
- Строго выведите формулу (6).
- Качественно объясните следующий «парадокс». В поле плоского конденсатора неоднозначно определен потенциал «бесконечности»: при движении в положительном направлении оси Z потенциал «бесконечности» оказался равным -φ0; при движении в отрицательном направлении оси Z - +φ0 , при движении вдоль осей X или Y- равен нулю. Так чему равен потенциал «бесконечности» в реальной системе двух пластин конечных размеров?
Примечания
- ↑ Такая система называется плоским конденсатором, подробнее эти устройства мы будем изучать позже.
Смотреть HD
видео онлайн
бесплатно 2022 года