Слободянюк А.И. Физика 10/9.7

Содержание книги

Предыдующая страница

§9. Электрическое поле и его свойства

9.7. Поле равномерно заряженной сферы

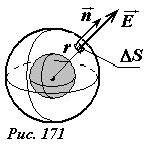
Рассмотрим теперь с помощью теоремы Гаусса, поле, создаваемое равномерно заряженной тонкой сферической оболочки. Опять начнем с рассмотрения симметрии поля. Очевидно, что поле, также как распределение зарядов имеет сферическую симметрию. Это означает, что модуль вектора напряженности зависит только от расстояния до центра сферы (или во всех точках, находящихся от центра сферы на одном расстоянии, модуль напряженности постоянен), а направление — радиальное, от центра сферы к точке наблюдения. Выберем в качестве замкнутой поверхности, к которой применим теорему Гаусса, сферу, концентрическую с заряженной оболочкой (рис. 171).

Пусть радиус сферы r больше радиуса оболочки. Тогда во всех точках этой сферы вектор напряженности направлен вдоль нормали к поверхности, а его модуль постоянен. Поэтому поток вектора напряженности через сферу равен произведению модуля напряженности на площадь сферы \(~\Phi_E = E \cdot 4 \pi r^2\) . По теореме Гаусса это поток равен заряду сферы, деленному на электрическую постоянную \(~\Phi_E = \frac{Q}{\varepsilon_0}\) . Из равенства этих выражений получаем зависимость напряженности поля от расстояния

\(~E = \frac{Q}{4 \pi \varepsilon_0 r^2}\) . (1)

Полученная формула, соответствует формуле закона Кулона для точечного заряда, следовательно, вне сферы, поле равномерно заряженной сферы, совпадает с полем точечного заряда, помещенного в центре сферы. Таким образом, результат, на доказательство которого И. Ньютон затратил несколько лет, получен нами почти автоматически. Подчеркнем, что для доказательства формулы (1) помимо теоремы К. Гаусса, потребовалось рассмотреть симметрию поля.

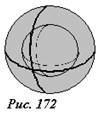
Поле внутри заряженной сферической оболочки также должно обладать сферической симметрией. Поэтому, поток вектора напряженности электрического поля через сферу, концентрическую с заряженной оболочкой и расположенную внутри нее (рис. 172) также выражается формулой \(~\Phi_E = E \cdot 4 \pi r^2\) .

Однако внутри этой сферы электрических зарядов нет, поэтому, из теоремы К. Гаусса следует, что напряженность поля внутри сферы равна нулю. Подчеркнем, если бы теорема Гаусса была не справедлива, то внутри равномерно заряженной оболочки существовало бы электрическое поле.

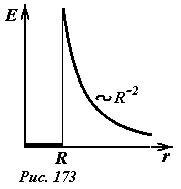
Таким образом, функция, описывающая напряженность поля равномерно заряженной сферы радиуса R, имеет вид (график этой функции показан на рисунке 173)

\(~E(r) = \left\{ \begin{matrix} 0, & \mbox{npu } r < R \\ \frac{Q}{4 \pi \varepsilon_0 r^2}, & \mbox{npu } r > R \end{matrix} \right.\) .

Следующая страница