Решение. Относительность движения. B7

Условие

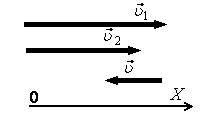
B7. На рисунке 1 даны направления движения трех тел. Модули скоростей первого и второго тела относительно неподвижного наблюдателя соответственно равны: υ₁ = 5 м/с, υ₂ = 4 м/с. Скорость третьего тела относительно второго по модулю равна υ₃ = 3 м/с. Определите скорость третьего тела относительно:

а) неподвижного наблюдателя;

б) первого тела.

Рис. 1

Решение

а) 1 способ. Так как задана скорость движения тела 3 относительно тела 2, то переходим в СО, связанную с телом 2. Тогда υ_c =υ₂ = 4 м/с; υ_top3 = υ = 3 м/с; найти необходимо скорости тела относительно неподвижной системы отсчета, т.е. υ_ton3 – ?

Запишем закон сложения скоростей в следующем виде\[~\vec \upsilon_{ton3} = \vec \upsilon_c + \vec \upsilon_{top3} = \vec \upsilon_2 + \vec \upsilon\] .

В проекциях на ось 0Х: υ_ton3 = υ₂ – υ; υ_ton3 = 4 м/с – 3 м/с = 1 м/с.

«ИНТУИТИВНО» тело 3 движется относительно тела 2 с меньшей скоростью, чем скорость тела 2, следовательно тело 3 движется в ту же сторону, что и второе тело. Так как скорость относительного движения направлена против скорости системы, то скорость тела 3 меньше скорости тела 2.

2 способ. Так как задана скорость движения тела 3 относительно тела 2, то воспользуемся законом сложения скоростей в следующем виде\[~\vec \upsilon_3 = \vec \upsilon_2 + \vec \upsilon_{3/2}\] или в проекции на ось 0Х: υ_3x = υ₂ – υ_3/2; υ_3x = 4 м/с – 3 м/с = 1 м/с.

б) 1 способ. Определим скорость тела 3 относительно тела 1 (υ_top3x). Для этого переходим в СО, связанную с первым телом. Тогда υ_c =υ₁ = 5 м/с; найти необходимо υ_top3x – ?

Из закона сложения скоростей \(~\vec \upsilon_{ton3} = \vec \upsilon_c + \vec \upsilon_{top3}\) следует, что \(~\vec \upsilon_{top3} = \vec \upsilon_{ton3} - \vec \upsilon_c = \vec \upsilon_{ton3} - \vec \upsilon_1\) , где \(~\vec \upsilon_{ton3}\) – скорость тела 3 относительно неподвижного наблюдателя (υ_ton3x = 1 м/с (см. пункт а 1 способ)).

В проекциях на ось 0Х: υ_top3x = υ_ton3x – υ₁; υ_top3x = 1 м/с – 5 м/с = –4 м/с. Знак «–» указывает на то, что данная скорость направлена против выбранной оси 0Х.

«ИНТУИТИВНО» – тело 1 и тело 3 движутся в одну сторону, поэтому их относительная скорость будет меньше их реальной скорости. А так как скорость третьего тела меньше скорости первого тела, то тело 3 будет отставать от тела 1, и ее скорость будет направлена против скорости первого тела.

2 способ. Так как определяем скорость движения тела 3 относительно тела 1, то воспользуемся законом сложения скоростей в следующем виде\[~\vec \upsilon_3 = \vec \upsilon_1 + \vec \upsilon_{3/1}\] . Тогда \(~\vec \upsilon_{3/1} = \vec \upsilon_3 - \vec \upsilon_1\) или в проекции на ось 0Х: υ_3/1x = υ_3x – υ₁, где υ_3x = 1 м/с (см. пункт а 2 способ). Получаем υ_3/1x = 1 м/с – 5 м/с = –4 м/с.