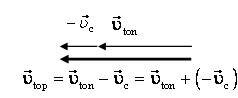Решение. Относительность движения. B9

Условие

B9. Скорость велосипедиста 36 км/ч, а скорость встречного ветра 4 м/с. Какова скорость ветра в системе отсчета, связанной с велосипедистом?

Решение

1 способ. Решим задачу по предложенному плану.

План решения задач:	Решение
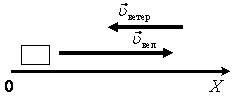
1. Сделайте чертеж: тела изобразите в виде прямоугольников, над ними укажите направление скорости.	Рис. 1
2. Выберите направление осей координат.
3. Исходя из условия задачи или по ходу решения:
а) определите тело, скорость которого надо найти;	Ветер.
б) определите тело, с которым свяжем неподвижную СО;	Земля.
в) определите тело, с которым свяжем подвижную СО и объясните свой выбор;	Велосипедист, т.к. несмотря на то, что движутся два тела (велосипедист и ветер), нужно определить скорость ветра относительно велосипедиста.
г) найдите скорость системы и объясните свой выбор;	υc = υвел = 36 км/ч = 10 м/с, т.к. это скорость тела, с которым мы связали подвижную систему.
д) найдите скорость тела относительно неподвижной СО и объясните свой выбор;	υton = υветер = 4 м/с, т.к. скорость ветра задана относительно земли (нет специальных оговорок), с которой мы связали неподвижную систему.
е) найдите скорость тела относительно подвижной СО и объясните свой выбор.	Это скорость ветра относительно велосипедиста, с которым мы связали подвижную систему. По условию эту скорость нужно найти.
4. Запишите закон сложения скоростей в векторном виде.	\(~\vec \upsilon_{ton} = \vec \upsilon_c + \vec \upsilon_{top}\)
5. Найдите искомые величины.	Способ а. Найдем проекцию скоростей на ось 0X: -υton = υc + υtopx(рис. 1), вектор скорости \(~\vec \upsilon_{ton}\) направлен против оси. После преобразований получим υtop x = –υton – υc = –υветер – υвел. Тогда υtopx = –4 м/с – 10 м/с = –14 м/с. Знак «–» указывает, что проекция скорости отрицательная, т.е. вектор \(~\vec \upsilon_{top}\) направлен против выбранной оси 0Х. Способ б. Найдем векторную сумму скоростей. Из рисунка 2 видно, что значение υton = υc + υtop = υветер +υвел. Рис. 2 Тогда υtop = 4 м/с + 10 м/с = 14 м/с.

2 способ. Так как требуется найти скорость ветра в системе отсчета, связанной с велосипедистом, то воспользуемся законом сложения скоростей в следующем виде\[~\vec \upsilon_{vet} = \vec \upsilon_{vel} + \vec \upsilon_{vet/vel}\] , где υ_vet = 4 м/с – скорость ветра, по умолчанию, относительно земли (неподвижной СО); υ_vel = 36 км/ч = 10 м/с – скорость велосипедиста, по умолчанию, относительно земли (неподвижной СО); υ_vet/vel – скорость ветра в системе отсчета, связанной с велосипедистом, по условию эту скорость нужно найти. Тогда \(~\vec \upsilon_{vet/vel} = \vec \upsilon_{vet} - \vec \upsilon_{vel}\) или в проекции на ось 0Х:

υ_{vet/vel x} = –υ_vet – υ_vel; υ_{vet/vel x} = –4 м/с – 10 м/с = –14 м/с. Знак «–» указывает, что проекция скорости отрицательная, т.е. вектор направлен против выбранной оси 0Х.