Решение. Сила упругости. B17

Условие

B17. Постройте график зависимости удлинения пружины от приложенной силы Δl = f(F), если коэффициент жесткости пружины 400 Н/м.

Решение

Для неподвижной пружины сила упругости, возникающая при деформации, равна приложенной силе F_упр = F.

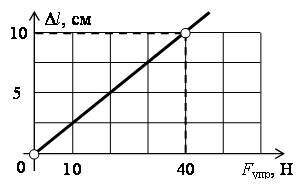
Уравнение зависимости силы упругости, возникающей в деформированной пружине, от ее удлинения F_упр = k∙Δl, где k = 400 Н/м. Тогда уравнение зависимости удлинения пружины от приложенной силы примет вид \(~\Delta l = \frac{1}{400} \cdot F = 2,5 \cdot 10^{-3} \cdot F\) . Это линейная функция, проходящая через начало координат. Для построения такой прямой достаточно одной точки.

Для заполнения таблицы выбираем произвольные значения силы. Пусть, например, F = 40 Н. Получаем Δl(4 Н) = 2,5∙10^-3 ∙ 40 = 1∙10^-1 (м) = 10 см. Подставляем эти значения в таблицу:

Δl, см	0	10
Fупр, Н	0	40

По оси ординат откладывают значения функции (Δl), по оси абсцисс – аргумента (F). Отметим полученные точки и соедините их прямой линией. Полученный график изображен на рис. 1.

Рис. 1