Слободянюк А.И. Физика 10/16.9

Содержание книги

Предыдующая страница

§16. Превращение энергии в электрических и магнитных явлениях

16.9 Превращения энергии при изменении индуктивности цепи.

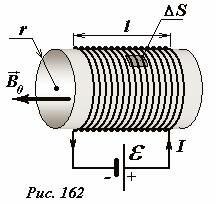
Энергия магнитного поля соленоида зависит от индуктивности последнего. Поэтому при изменении размеров соленоида или изменении материала сердечника в цепи происходят процессы, приводящие к изменению энергии магнитного поля. Для поддержания постоянного электрического тока в цепи, содержащей соленоид, присутствие источника ЭДС обязательно (Рис. 162). Следовательно, нам необходимо принимать во внимание не только изменения магнитного поля соленоида, но и процессы, протекающие на других участках цепи, в том числе и источнике.

Рассмотрим подробно превращения энергии при изменении радиуса соленоида. Для наглядности можно считать, что обмотка соленоида изготовлена из упругой проволоки, способной растягиваться. Прежде всего, обратим внимание, что на обмотку соленоида действуют силы со стороны магнитного поля, создаваемого электрическим током в самой обмотке.

Найдем силы, действующие на обмотку длинного соленоида с плотной намоткой, для которого можно пренебречь краевыми эффектами. Магнитное поле внутри такого соленоида является однородным, вектор индукции направлен вдоль оси соленоида, а его модуль равен

\(~B_0 = \mu_0 nI\) , (1)

где \(~n = \frac{N}{l}\) - плотность намотки, равная числу витков на единицу длины соленоида, I - сила тока в обмотке. Вне соленоида магнитное поле отсутствует.

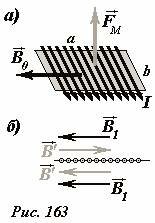
Выделим на поверхности соленоида малую площадку площадью \(\Delta S = ab\) (Рис. 163а). Сила Ампера, действующие на участки витков обмотки, находящиеся на выделенной площадке, направлена перпендикулярно направлению тока и вектору индукции поля. Модуль этой силы рассчитывается по формуле

\(~F = I N_1 B_1 b\) , (2)

где \(N_1 = na\) - число витков, лежащих на площадке, B₁ - индукция магнитного поля, создаваемого всеми элементами соленоида, кроме лежащих на площадке.

Вспомните расчет силы, действующей на заряженную пластину конденсатора со стороны электрического поля. При выводе формулы для этой силы мы также учитывали напряженность поля, создаваемого всеми зарядами, кроме находящихся на площадке. Мы показали, что напряженность этого поля в два раза меньше напряженности суммарного поля.

Чтобы определить требуемую индукцию поля, представим суммарное поле в виде суммы полей\[~\vec B'\] - создаваемого током площадки и \(~\vec B_1\) - создаваемого всеми остальными участками обмотки (Рис. 163б). Внутри соленоида эти векторы направлены одинаково и их сумма равна индукции суммарного поля \(B' + B_1 = B_0\). Вне соленоида эти векторы направлены противоположно и их сумма равна нулю \(B' - B_1 = 0\). Из этих соотношений следует, что индукция поля, действующего на выделенную площадку, в два раза меньше индукции суммарного поля внутри соленоида \(~B_1 = \frac{B_0}{2}\). Таким образом, на выделенную площадку действует сила, которая рассчитывается по формулам

\(~F = I N_1 B_1 b = I n \frac{B_0}{2} ab = \frac{\mu_0 n^2 I^2}{2} ab = \frac{(\mu_0 n I)^2}{2 \mu_0} ab = \frac{B^2_0}{2 \mu_0} ab\) . (3)

Найденная сила пропорциональна площади выделенной площадки и направлена перпендикулярно ей, поэтому можно говорить о давлении магнитного поля на поверхность соленоида. Существенно, что величина этого давления равна плотности энергии магнитного поля вблизи площадки

\(~p = \frac{F}{\Delta S} = \frac{B^2_0}{2 \mu_0} = w_M\) . (4)

аналогично тому, что давление электрического поля на поверхность проводника со стороны электрического поля равно плотности энергии этого поля.

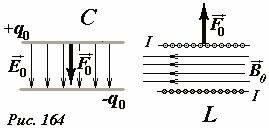
Продолжим сравнение действия электрического поля в конденсаторе и магнитного поля в соленоиде. Самое существенное отличие заключается в направлении действия силы (Рис. 164). На обкладки конденсатора действует сила, направленная внутрь, в сторону части пространства, занятого полем. Если предоставить пластинам возможность двигаться, то сила их взаимодействия приведет к уменьшению расстояния между пластинами, уменьшению объема, занятого полем, уменьшению суммарной энергии поля (при неизменном заряде на пластКурсивное начертаниеинах). При этом энергия электрического поля переходит в кинетическую энергию движущихся пластин.

На обмотку соленоида со стороны магнитного поля действует сила, направленная наружу, в сторону противоположную части пространства, занятого полем. Если обмотка соленоида способна расширятся, то силы взаимодействия приведут к увеличению радиуса обмотки, увеличению объема, занятого полем, увеличению его суммарной энергии (при неизменной силе тока в обмотке). Таким образом, мы приходим к парадоксальному выводу: магнитное поле совершает работу и при этом его энергия увеличивается – отсюда уже недалеко до «вечного двигателя»! Не стоит обольщаться этим «гениальным изобретением», достаточно вспомнить, что для поддержания тока в цепи, в ней должен быть источник, обладающий энергией и отдающий ее в цепь. Кроме того, при движении зараженной пластины в электрическом поле распределение зарядов и их величина могут оставаться неизменными. При движении проводника в магнитном поле распределение электрических токов и их величина изменяются вследствие явления электромагнитной индукции.

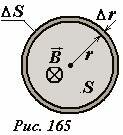
Рассмотрим, какие изменения произойдут в рассматриваемой системе, показанной на рис. 162, при увеличении радиуса обмотки на малую величину Δr (то есть при увеличении площади сечения на величину ΔS - Рис. 165). Изменение силы тока в цепи описывается уравнением закона Ома для полной цепи

\(~\varepsilon + \varepsilon_{ind} = IR\) , (5)

где R - полное сопротивление цепи, ε_ind - ЭДС индукции, возникающей в соленоиде, которая определяется законом Фарадея

\(~\varepsilon_{ind} = -\frac{\Delta \Phi}{\Delta t}\) , (6)

где \(~\Phi = NSB = nlS (\mu_0 n I) = \mu_0 n^2 lSI\) - магнитный поток через все N витков катушки (l - длина обмотки). На основании этих законов запишем уравнение

\(~\varepsilon = IR + \frac{\Delta \Phi}{\Delta t}\) ,

которое, как обычно, умножим на малую величину заряда Δq, протекающего по цепи за малый промежуток времени Δt, в результате получим соотношение

\(~\varepsilon \Delta q = IR \Delta q + \frac{\Delta \Phi}{\Delta t} \Delta q = IR \Delta q + I \Delta \Phi\) . (7)

В данном случае поток через соленоид может изменяться по двум причинам – изменения силы тока и изменения площади поперечного сечения соленоида. Пусть в некоторый момент времени сила тока в обмотке равнялась I, а площадь сечения S, затем за малый промежуток времени Δt сила тока изменилась на ΔI, а площадь - на ΔS. Тогда изменения магнитного потока можно представить в виде

\(~\Delta \Phi = \mu_0 n^2 l \Delta(IS) = \mu_0 n^2 l ((I + \Delta I)(S + \Delta S) - IS) = \mu_0 n^2 l (S \Delta I + I\Delta S)\) ,

на последнем шаге преобразований мы пренебрегли произведением малых величин ΔIΔS. Подставим полученное выражение в уравнение (7)

\(~\varepsilon \Delta q = IR \Delta q + I \Delta \Phi = IR \Delta q + I \mu_0 n^2 l (S \Delta I + I\Delta S) = IR \Delta q + \mu_0 n^2 l S I \Delta I + \mu_0 n^2 I^2 l \Delta S\) . (8)

Выясним теперь смысл каждого члена этого уравнения, тем более, что некоторые из них уже встречались нам ранее: \[\varepsilon \Delta q\] - работа источника ЭДС по перемещению заряда Δq; \[~IR \Delta q = I^2 R \Delta t\] - количество теплоты, выделившееся в цепи при прохождении заряда Δq; \[~\mu_0 n^2 l S I \Delta I = \mu_0 n^2 \Delta \left( \frac{I^2}{2}\right) Sl = \Delta \left( \frac{\mu_0 n^2 I^2}{2}\right) Sl = \Delta \left( \frac{B^2}{2\mu_0}\right) Sl\] - (здесь \(B = \mu_0 n I\) - индукция магнитного поля внутри соленоида) изменение энергии магнитного поля вследствие изменения силы тока в соленоиде (изменение энергии поля в первоначальном объеме соленоида);

наконец, последнее слагаемое преобразуется к виду \(~\mu_0 n^2 I^2 l \Delta S = 2 \left( \frac{B^2}{2\mu_0}\right) \Delta V\) и равно удвоенной (!?) энергии магнитного поля в части приращенного объема соленоида ΔV. Смысл половины этого слагаемого, то есть \(~\left( \frac{B^2}{2\mu_0}\right) \Delta V\) , понятен – это увеличение энергии поля вследствие увеличения его объема, осталось найти смысл оставшейся величины \(~\left( \frac{B^2}{2\mu_0}\right) \Delta V\) . Мы не случайно начали рассуждения данного раздела рассмотрения сил, действующих на обмотку – эти силы увеличивают размер соленоида, следовательно, совершают работу. В результате совершения этой работы увеличивается механическая энергия обмотки – если она упругая и деформируемая, то увеличивается энергия ее упругой деформации, возможно, что часть этой энергии идет на увеличение кинетической энергии расширяющихся витков. Выяснение этих деталей требует более конкретного описания механических свойств обмотки. Не будем их конкретизировать, покажем, что оставшееся слагаемое действительно равно работе сил поля над расширяющейся обмоткой. Еще раз взглянем на выделенную на боковой поверхности соленоида площадку (Рис. 162, 163) со сторонами a и b, на нее действует сила pab (p - давление поля). При смещении этой площадки на расстояние Δr в направлении действия силы, магнитное поле совершает работу \(~\delta A = F \Delta r = pab \Delta r = p \Delta V_{ab}\) , где \(\Delta V_{ab}\) - изменение объема соленоида при смещении рассматриваемой площадки. Так как давление на все точки поверхности соленоида одинаково, то суммарная работа поля по смещению всех участков его поверхности будет равна \(A = p \Delta V\) , где ΔV - полное изменение объема соленоида. Используя формулу (4) для давления магнитного поля, получим, что работа по расширению соленоида равна

\(~A = \left( \frac{B^2}{2\mu_0}\right) \Delta V\) .

Таким образом, энергетический баланс и в этом случае сходится: работа, совершенная источником ЭДС по перемещению заряда \(\varepsilon \Delta q\), расходуется на:

- преодоление сил сопротивления (в результате чего выделяется теплота \(\delta Q = IR \Delta q\));

- увеличение энергии поля, как вследствие изменения его индукции (и плотности энергии) \(~\Delta W_B = \Delta \left( \frac{B^2}{2\mu_0}\right) V\) , так и вследствие изменения объема, занятого полем \(~\Delta W_V = \left( \frac{B^2}{2\mu_0}\right) \Delta V\);

- увеличение механической энергии обмотки, которая возрастает благодаря работе поля \(~\Delta W_{obm} = A = \left( \frac{B^2}{2\mu_0}\right) \Delta V\).

Следующая страница