Слободянюк А.И. Физика 10/2.2. Средняя и мгновенная скорость при движении точки по прямой
Материал из PhysBook
§2. Кинематическое описание механического движения материальной точки
2.2 Средняя и мгновенная скорость при движении точки по прямой
Как мы уже отмечали, равномерное движение является простейшей моделью механического движения. Если такая модель неприменима, то необходимо использовать более сложные модели. Для их построение нам необходимо рассмотреть понятие скорости в случае неравномерного движения.
Пусть за интервал времени от t0 до t1 координата точки изменилась от x0 до x1. Если мы вычислим скорость по прежнему правилу
 , (1)
, (1)
то получим величину (она называется средней скоростью), которая описывает быстроту движения «в среднем» - вполне возможно, что за первую половину времени движения точка сместилась на большее расстояние, чем за вторую.
Средней скоростью называется физическая величина равная отношению изменения координаты точки к интервалу времени, в течение которого это изменение произошло.
Геометрический смысл средней скорости - коэффициент наклона секущей AB графика закона движения.
Для более детального, более точного описания движения, можно задать два значения средней скорости – за первую половину времени движения υср1, за вторую половину - υср2 .Если и такая точность нас не устраивает - то необходимо дробить временные интервалы дальше - на четыре, восемь и т.д. частей. При этом необходимо задавать соответственно четыре, восемь и т.д. значений средних скоростей. Согласитесь, такое описание становится громоздким и неудобным. Выход из этой ситуации давно найден - он заключается в том, что бы рассматривать скорость как функцию времени.
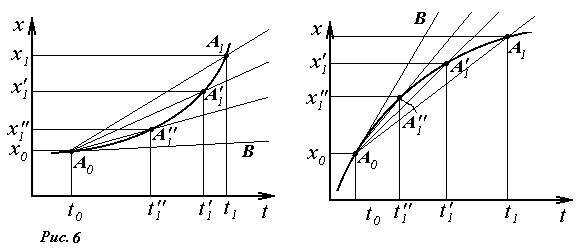
Давайте посмотрим, как будет меняться средняя скорость при уменьшении промежутка времени, за который мы эту скорость вычисляем. На рис.6 показан график зависимости координаты материальной точки от времени. Будем вычислять среднюю скорость за интервал времени от t0 до t1, последовательно приближая значение t1 к t0. При этом семейство секущих A0A1, A0A1’, A0A1’’ (рис.6), будет стремиться к некоторому предельному положению прямой A0B, которая является касательной к графику закона движения. Мы приводим два различных случая, чтобы показать, что мгновенная скорость может быть как больше, так и меньше средней скорости. Эту процедуру можно описать и алгебраически, последовательно вычисляя отношения  ,
,  ,
,  . При этом оказывается, что эти величины приближаются к некоторому вполне определенному значению. Это предельное значение получило название мгновенной скорости.
. При этом оказывается, что эти величины приближаются к некоторому вполне определенному значению. Это предельное значение получило название мгновенной скорости.
Мгновенной скоростью называется отношение изменения координаты точки к интервалу времени, за которое это изменение произошло, при интервале времени, стремящемся к нулю [1]:
 , при Δt → 0 . (2)
, при Δt → 0 . (2)
Геометрический смысл мгновенной скорости - коэффициент наклона касательной к графику закона движения.
Таким образом, мы «привязали» значение мгновенной скорости к конкретному моменту времени - задали значение скорости в данный момент времени, в данной точке пространства. Тем самым у нас появилась возможность рассматривать скорость тела как функцию времени, или функцию координаты.
С математической точки зрения это гораздо удобней, чем задавать значения средних скоростей на многих малых временных промежутках. Однако давайте задумаемся, а имеет ли физический смысл скорость в данный момент времени? Скорость - характеристика движения, в данном случае перемещения тела в пространстве. Для того чтобы зафиксировать перемещение необходимо наблюдать за движением в течение некоторого промежутка времени. Чтобы измерить скорость, также необходим промежуток времени. Даже самые совершенные измерители скорости радарные установки измеряют скорость движущихся автомобилей пусть за малый (порядка одной миллионной доли секунды) промежуток времени, а не в какой-то момент времени. Следовательно, выражение «скорость в данный момент времени» с точки зрения физики некорректно. Тем не менее, в механике постоянно пользуются понятием мгновенной скорости, которое очень удобно в математических расчетах. Математически, логически мы можем рассмотреть предельный переход Δt → 0, а физически имеется минимально возможное значение промежутка Δt, за который можно измерить скорость.
В дальнейшем, говоря о скорости, мы будем иметь в виду именно мгновенную скорость. Заметим, при равномерном движении мгновенная скорость равна ранее определенной скорости, потому, что при равномерном движении отношение  не зависит от величины промежутка времени, поэтому остается неизменным и при сколь угодно малом Δt.
не зависит от величины промежутка времени, поэтому остается неизменным и при сколь угодно малом Δt.
Так как скорость может зависеть от времени, то ее следует рассматривать как функцию времени, и изображать ее в виде графика.
Примечания
- ↑ В высшей математике это определение записывают с помощью специального символа lim (предел - limit):
 , кроме того, процедура вычисления подобного предела называется взятием производной.
, кроме того, процедура вычисления подобного предела называется взятием производной.
Смотреть HD
видео онлайн
бесплатно 2022 года
