Т. Закон Ома для пер. тока — различия между версиями
|
Ruslan (обсуждение | вклад)
|
Ruslan (обсуждение | вклад)
|
||
| Строка 1: | Строка 1: | ||
| + |
__NOTOC__
|
||
|
== Закон Ома для участка цепи переменного тока. Разность фаз между колебаниями силы тока и напряжения ==
|
== Закон Ома для участка цепи переменного тока. Разность фаз между колебаниями силы тока и напряжения ==
|
||
| Строка 18: | Строка 19: | ||
|
[[Изображение:Img_T-116-002.jpg|frame|center|<center>Рис. 2</center>]]
|
[[Изображение:Img_T-116-002.jpg|frame|center|<center>Рис. 2</center>]]
|
||
| − |
Амплитудное значение силы тока <math>~I_0</math> в цепи совпадает по фазе с амплитудным значением напряжения <math>~U_{0R}</math> на резисторе ''R''. Амплитуда <math>~(U_0)</math> приложенного напряжения должна быть равна геометрической сумме этих амплитуд. Угол φ определяет разность фаз между напряжением и силой тока <math>~I = I_0\cos (wt -\
|
+ |
Амплитудное значение силы тока <math>~I_0</math> в цепи совпадает по фазе с амплитудным значением напряжения <math>~U_{0R}</math> на резисторе ''R''. Амплитуда <math>~(U_0)</math> приложенного напряжения должна быть равна геометрической сумме этих амплитуд. Угол φ определяет разность фаз между напряжением и силой тока <math>~I = I_0\cos (wt -\varphi).</math> Из рисунка 2 видно, что <math>~\operatorname{tg} \varphi = \frac {U_{0L} - U_{0C}}{U_{0C}} = \frac {wL - \frac 1{wC}}{R}.</math>
|
|
По теореме Пифагора
|
По теореме Пифагора
|
||
Версия 21:29, 6 октября 2010
Закон Ома для участка цепи переменного тока. Разность фаз между колебаниями силы тока и напряжения
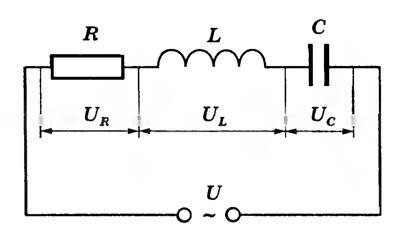
Рассмотрим участок цепи, содержащий резистор сопротивлением R, катушку индуктивностью L и конденсатор емкостью С, включенные последовательно (рис. 1). На участок подается переменное напряжение \(~U = U_0 \sin wt,\) в результате возникает переменный ток.
Так как электромагнитные взаимодействия распространяются со скоростью света, то во всех последовательно включенных элементах цепи изменения силы тока происходят практически одновременно. Колебания же мгновенных значений напряжения на каждом из элементов \(~U_R, U_L, U_C \) не совпадают по фазе с колебаниями силы тока. В любой момент времени сумма мгновенных значений напряжений на последовательно включенных элементах цепи равна мгновенному значению приложенного напряжения:
Учитывая, что на активном сопротивлении колебания силы тока совпадают, на емкостном опережают, на индуктивном отстают от колебаний напряжения (см. Переменный ток, Реактивные сопротивления), последнее равенство можно записать
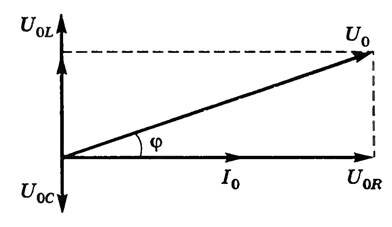
Амплитуду колебаний напряжения в цепи можно выразить через амплитудные значения напряжения на отдельных ее элементах, воспользовавшись методом векторных диаграмм. На рисунке 2 представлена векторная диаграмма амплитуд напряжений на резисторе \(~(U_{0R})\) конденсаторе \(~(U_{0C})\) и катушке \(~(U_{0L})\).
Амплитудное значение силы тока \(~I_0\) в цепи совпадает по фазе с амплитудным значением напряжения \(~U_{0R}\) на резисторе R. Амплитуда \(~(U_0)\) приложенного напряжения должна быть равна геометрической сумме этих амплитуд. Угол φ определяет разность фаз между напряжением и силой тока \(~I = I_0\cos (wt -\varphi).\) Из рисунка 2 видно, что \(~\operatorname{tg} \varphi = \frac {U_{0L} - U_{0C}}{U_{0C}} = \frac {wL - \frac 1{wC}}{R}.\)
По теореме Пифагора
\(~I_0 = \frac {U_0}{\sqrt{R^2 + (wL - \frac 1{wC})^2}}\) — закон Ома для участка цепи переменного тока.
Величина \(~Z = \sqrt{R^2 + (wL - \frac 1{wC})^2} \) называется полным сопротивлением цепи, \(~(wL - \frac 1{wC})\) — реактивным сопротивлением.
Резонанс в электрической цепи
Резонанс напряжений
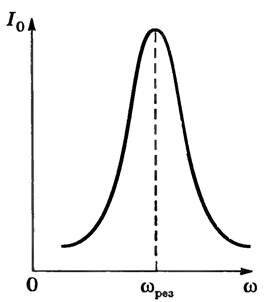
Если в цепи (см. рис. 1) подобрать так емкость С конденсатора и индуктивность катушки, чтобы \(~wL = \frac 1{wC}, \) то разность фаз между колебаниями силы тока и напряжения φ = 0, т.е. изменения тока и напряжения происходят синфазно. Из этого равенства \(~w_{rez} = \frac 1{\sqrt {LC}}.\) Эту частоту называют резонансной. При этом условии Z = R, т.е. полное сопротивление цепи становится наименьшим, амплитуда силы тока при данном напряжении принимает наибольшее значение (рис. 3).
В этом случае амплитуда напряжения на активном сопротивлении равна амплитуде внешнего напряжения, приложенного к участку цепи \(~(U_{0R} = U_0),\) а напряжения на катушке индуктивности и конденсаторе одинаковы по модулю и противоположны по фазе:
При этом \(~(U_{OL})_{rez} = (U_{OC})_{rez},\) и они могут значительно превышать \(~U_0.\) Это явление называется резонансом напряжений. Резонанс используется в радио- и электротехнике для усиления колебаний напряжения какой-либо определенной частоты. Его надо учитывать при расчете изоляции электрических линий, содержащих катушки индуктивности и конденсатора, иначе может наблюдаться их пробой.
Резонанс токов
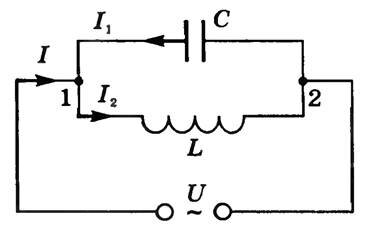
Рассмотрим участок цепи переменного тока, содержащий параллельно включенные конденсатор емкостью С и катушку индуктивностью L (рис. 4).
Пусть активное сопротивление мало, им можно пренебречь. Если приложенное напряжение изменяется по закону \(~U=U_0 \sin wt,\), то в ветви 1С2 проходит ток
В ветви 1L2 проходит ток
Таким образом, разность фаз токов в ветвях 1С2 и 1L2 равна π, т.е. колебания токов в ветвях противоположны по фазе. Амплитуда тока во внешней (неразветвленной) цепи \(~I_{0C} = \left| I_{01} - I_{02} \right| = U_0 (wC - \frac 1 {wL}).\) Если \(~w = w_{rez} = \frac 1{\sqrt {LC}},\) то \(~I_{01} = I_{02}\) и \(~I_0 = 0.\) Амплитуда силы тока \(~I_0\) оказалась равной нулю потому, что активным сопротивлением участка пренебрегали. Если учесть сопротивление R, то разность фаз не будет равна π и \(~I_0 \not = 0,\) но \(~I_0\) примет наименьшее возможное значение, а амплитуды сил токов \(~I_{01} \) и \(~I_{02}\) могут значительно превышать амплитуду силы тока \(~I_0.\)
Явление резкого уменьшения амплитуды силы тока во внешней цепи, питающей параллельно включенные конденсатор и катушку индуктивности, при приближении частоты w приложенного напряжения к резонансной частоте wrez называется резонансом токов (параллельным резонансом).
Это явление используется в резонансных усилителях, позволяющих выделять одно определенное колебание из сигнала сложной формы, а также в индукционных печах, где параллельно нагревательной катушке включается конденсатор, емкость которого подбирается так, чтобы при частоте генератора получился резонанс токов, в результате сила тока через катушку будет гораздо больше, чем сила тока в подводящих проводах.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 406-408.
Смотреть HD
видео онлайн
бесплатно 2022 года