Т. ЭДС индукции в движ. проводниках — различия между версиями
|
Ruslan (обсуждение | вклад)
|
Ruslan (обсуждение | вклад)
|
||
| Строка 8: | Строка 8: | ||
| − |
Пусть средняя скорость упорядоченного движения электронов, обусловленная действием силы Лоренца, в системе отсчета, связанная с проводником, равна <math>~\vec u </math>. Тогда скорость <math>~\vec {v_0}</math> движения электронов в инерциальной системе отсчета, в которой существует магнитное поле, будет равна <math>~\vec{v_0} = \vec u + \vec v</math>, причем вектор <math>~\vec {v_0}</math> составляет угол α со скоростью <math>~\vec v</math> движения проводника. Сила Лоренца будет перпендикулярна <math>~\vec {v_0}</math> (рис. 1, б), и ее модуль <math>~F_L = qBv_0</math>. Разложим вектор <math>~\vec {F_L}</math> на две составляющие: направленные вдоль проводника <math>~\vec
|
+ |
Пусть средняя скорость упорядоченного движения электронов, обусловленная действием силы Лоренца, в системе отсчета, связанная с проводником, равна <math>~\vec u </math>. Тогда скорость <math>~\vec {v_0}</math> движения электронов в инерциальной системе отсчета, в которой существует магнитное поле, будет равна <math>~\vec{v_0} = \vec u + \vec v</math>, причем вектор <math>~\vec {v_0}</math> составляет угол α со скоростью <math>~\vec v</math> движения проводника. Сила Лоренца будет перпендикулярна <math>~\vec {v_0}</math> (рис. 1, б), и ее модуль <math>~F_L = qBv_0</math>. Разложим вектор <math>~\vec {F_L}</math> на две составляющие: направленные вдоль проводника <math>~\vec F_{L \parallel}</math> и перпендикулярно проводнику <math>~\vec F_{L \perp}</math>.
|
| − |
Продольная составляющая <math>~\vec
|
+ |
Продольная составляющая <math>~\vec F_{L \parallel}</math> и выполнит работу по разделению зарядов.
|
|
Из рис. 1, б видим, что <math>~F_{L \parallel} = F_L \cos \phi = qBv_0 \cos \phi</math>, а <math>~v_0 \cos \phi = v</math>. Следовательно, <math>~F_{L \parallel} = qBv</math>. Перемещение электронов прекратится, когда <math>~F_{L \parallel} = F_e </math>, т.е. <math>~ qBv = qE </math>. Напряженность электростатического поля связана
|
Из рис. 1, б видим, что <math>~F_{L \parallel} = F_L \cos \phi = qBv_0 \cos \phi</math>, а <math>~v_0 \cos \phi = v</math>. Следовательно, <math>~F_{L \parallel} = qBv</math>. Перемещение электронов прекратится, когда <math>~F_{L \parallel} = F_e </math>, т.е. <math>~ qBv = qE </math>. Напряженность электростатического поля связана
|
||
Версия 17:50, 8 сентября 2010
ЭДС индукции в движущихся проводниках
Выясним механизм возникновения ЭДС индукции в проводнике, движущемся в постоянном магнитном поле.
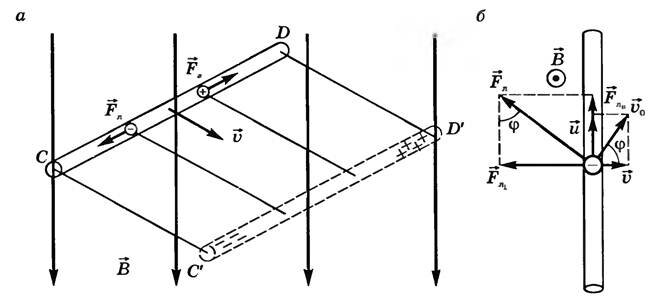
Пусть металлический проводник движется со скоростью \(~\vec v\), перпендикулярной вектору магнитной индукции \(~\vec B\) (рис. 1). Вместе с проводником, естественно, движутся свободные электроны. Следовательно, на электроны будет действовать сила Лоренца. Под действием этой силы свободные электроны перемещаются к одному из торцов проводника (на рис. 1, а к левому торцу), в результате происходит разделение зарядов: положительные заряды накапливаются на одном конце проводника, отрицательные — на другом. Эти заряды создадут внутри проводника электростатическое поле. Перераспределение зарядов будет происходить до тех пор, пока электрическая сила \(~\vec {F_e} = q \vec {E}\) не скомпенсирует силу Лоренца.
Пусть средняя скорость упорядоченного движения электронов, обусловленная действием силы Лоренца, в системе отсчета, связанная с проводником, равна \(~\vec u \). Тогда скорость \(~\vec {v_0}\) движения электронов в инерциальной системе отсчета, в которой существует магнитное поле, будет равна \(~\vec{v_0} = \vec u + \vec v\), причем вектор \(~\vec {v_0}\) составляет угол α со скоростью \(~\vec v\) движения проводника. Сила Лоренца будет перпендикулярна \(~\vec {v_0}\) (рис. 1, б), и ее модуль \(~F_L = qBv_0\). Разложим вектор \(~\vec {F_L}\) на две составляющие: направленные вдоль проводника \(~\vec F_{L \parallel}\) и перпендикулярно проводнику \(~\vec F_{L \perp}\).
Продольная составляющая \(~\vec F_{L \parallel}\) и выполнит работу по разделению зарядов.
Из рис. 1, б видим, что \(~F_{L \parallel} = F_L \cos \phi = qBv_0 \cos \phi\), а \(~v_0 \cos \phi = v\). Следовательно, \(~F_{L \parallel} = qBv\). Перемещение электронов прекратится, когда \(~F_{L \parallel} = F_e \), т.е. \(~ qBv = qE \). Напряженность электростатического поля связана с разностью потенциалов \(~ E = \frac Ul\). Из этих уравнений найдем \(~U = Bνl\). Таким образом, между концами проводника возникла разность потенциалов. Следовательно, сторонней силой, вызывающей разделение зарядов, является продольная составляющая силы Лоренца. Работа, которую совершает эта сила при перемещении электрического заряда (электрона) вдоль проводника, \(~ A_1 = F_{L \parallel} l = qBvl \). ЭДС индукции в этом случае \(~ \varepsilon _i =\frac Aq = Bνl.\)
Если такой проводник замкнуть, то в цепи пойдет индукционный ток, направление которого можно определить по правилу правой руки (оно является частным случаем правила Ленца):
если правую руку расположить вдоль проводника так, чтобы перпендикулярная составляющая магнитной индукции \(~\vec {B_{\perp}}\) входила в ладонь, а отогнутый большой палец показывал направление движения проводника, то четыре вытянутых пальца укажут направление индукционного тока в проводнике.
Если \(~\vec v\) не перпендикулярно \(~\vec B\), то
где α — угол между \(~\vec v\) и \(~\vec B\).
Пусть проводник перемещается в магнитном поле в направлении действия внешней силы \(~\vec F\). За время t, в течение которого электрон, движущийся со скоростью \(~\vec u\) вдоль проводника, пройдет расстояние \(~ l = ut\), проводник переместится на \(~\Delta r.\) \(~\Delta r = vt = v \frac lu\). Работа, которую совершит за это время перпендикулярная составляющая силы Лоренца,
Из рисунка 1, б \(~\sin \phi_0 = \frac u{v_0}\). Тогда \(~A_2 =-qBv_0 \frac u{v_0} v\frac lu = -qBvl.\)
Так как \(~A_2<0\), то происходит торможение движения проводника в магнитном поле. Для того чтобы проводник двигался равномерно, к нему необходимо приложить внешнюю силу, по модулю равную перпендикулярной составляющей силы Лоренца. Полная работа силы Лоренца \(~A = A_1-A_2=qBvl - qBvl = 0 .\) В данном случае имеет место превращение механической энергии источника внешней силы \(~\vec F\) в энергию индукционного тока. Это превращение происходит в соответствии с законом сохранения и превращения энергии.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 348-350.
Смотреть HD
видео онлайн
бесплатно 2022 года