Kvant. Абсолютная температура

Городецкий Е. Е. Абсолютная температура //Квант. — 1988. — № 9. — С. 60-62.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Теплота! Казалось бы, нет другой такой области физики, где фундаментальные идеи о строении вещества (все тела состоят из взаимодействующих друг с другом молекул, которые находятся в непрестанном движении) касались бы так тесно наших непосредственных ощущений. Но как долог и мучителен был путь понимания даже самых простых вещей. Например того, что происходит при нагревании или остывании тел, при контакте двух тел с разными температурами и т. п.

В этой заметке мы коснемся лишь двух основных моментов современного представления о тепловых явлениях с точки зрения молекулярного строения вещества.

Выделим небольшую, но все же макроскопическую часть какого-нибудь тела. Небольшую — это значит, что размеры выделенной области гораздо меньше размеров всего тела. Это нам нужно для того, чтобы в случаях, когда температура меняется вдоль тела, на протяжении нашей области ее всюду можно было бы считать одинаковой. С другой стороны, мы сказали, что область должна быть макроскопической. Это означает, что, несмотря на небольшие размеры, число частиц в ней должно быть все-таки очень большим.

Молекулы, заполняющие выделенную область, движутся с самыми разными скоростями, сталкиваются друг с другом, некоторые из них покидают область, а на их место приходят другие — в общем, идет сложная, можно даже сказать, суетливая жизнь. Понять эту безумную молекулярную «пляску», наблюдая за каждой молекулой отдельно,— занятие совершенно безнадежное, да и ненужное: мы все равно не знали бы, что делать с такой гигантской информацией. К счастью, именно сложность и запутанность молекулярного движения позволяют подойти к описанию ситуации совсем с другой стороны — с точки зрения теории вероятностей.

Предсказания этой теории очень специфичны. Она не может, например, предсказать, кто и с каким временем победит в десятикилометровой лыжной гонке на предстоящих в 1992 году Олимпийских играх. Однако, просмотрев результаты всех предыдущих игр, можно более или менее надежно сказать, что 1—2 % участников гонки покажут время, меньшее 29 минут, а 60—70 % уложатся в интервал от 29 до 31 минуты и т. д. Разумеется, на школьных соревнованиях уровень и распределение результатов будет другим. Вполне очевидно, что ранг соревнований определяет средний уровень результатов (и в этом смысле, как будет видно из дальнейшего, он похож на температуру).

Теория вероятностей, почти ничего не зная о единичных событиях, надежно предсказывает исход большого числа однотипных или повторяющихся событий. Понятно поэтому, что хаотически движущиеся и взаимодействующие друг с другом молекулы являются идеальным объектом для такой теории (теперь ясно, зачем число молекул в выделенной области должно было большим).

Обсудим такой вопрос: какая часть всех молекул, заполняющих нашу область, имеет скорость, близкую к какой-нибудь заданной скорости υ (или, говоря иначе, имеет скорость в интервале от υ до υ + Δυ)? Для того чтобы сформулировать вопрос точнее, обозначим число частиц, имеющих скорость в данном интервале, через ΔN(υ), а полное число частиц, находящихся в выделенной области, через N. Тогда нам нужно найти отношение \(~\frac{\Delta N(\upsilon)}{N}\).

Если величина допустимого разброса скоростей Δυ не слишком велика, то понятно, что ΔN(υ) должно быть пропорционально Δυ:

\(~\frac{\Delta N(\upsilon)}{N} = f(\upsilon) \Delta \upsilon\) .

Величина f(υ) называется функцией распределения молекул по скоростям и является важнейшей характеристикой любой макроскопической системы. Зная f(υ), мы можем оценить, сколько процентов всех молекул движутся со скоростью, близкой к такой-то скорости, а сколько — к такой и т. д.

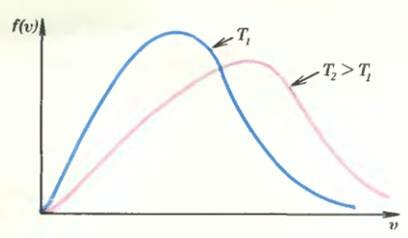
Напомним, что мы начали заметку с вопроса о том, что происходит с системой тел на уровне молекул в процессе выравнивания температур. Так вот, оказывается, что пока система не находится в равновесии, столкновения молекул приводят к постоянному изменению функции распределения f(υ), но после того как равновесие установилось, столкновения молекул больше не влияют на эту функцию. Явный вид равновесной функции f(υ) был найден теоретически в 1860 году выдающимся английским физиком Максвеллом.

Как следует из теории (внимание! это первое главное утверждение заметки), функция f(υ) в равновесии полностью определяется температурой системы Т. Этот факт, если вдуматься, кажется странным. Он означает, что система всегда сама придет в нужное состояние, независимо от того, что с ней было в начальный момент времени, лишь бы температура ее была задана. Вы можете «взболтать» газ как угодно, но, будучи предоставленным сам себе, он всегда придет в одно и то же состояние и начисто забудет о том, что с ним было вначале.

На рисунке представлены графики функции f(υ) для двух температур T₁ и T₂ (T₂ > T₁). Попробуйте самостоятельно объяснить факт «смещения» графика при изменении температуры.

Итак, температура играет основополагающую роль в определении теплового равновесия тел.

Из сказанного становится понятной и еще одна чрезвычайно важная вещь. Раз мы знаем, какая доля молекул с какой скоростью движется, мы можем вычислять средние характеристики движения молекул. В частности, среднюю энергию поступательного движения одной молекулы:

\(~\frac{\overline{m \upsilon^2}}{2} = \frac{3}{2} kT\) .

Основываясь на этой формуле, часто говорят, что температура является мерой средней кинетической энергии поступательного движения молекул. Это не совсем так. Дело в том, что коэффициент «\(~\frac{3}{2}\)», стоящий в выражении для энергии, совершенно не случаен и имеет глубокий смысл. Число «3» связано с тем, что в трехмерном пространстве для определения положения центра масс молекулы необходимо знать три его координаты. Или, говоря иначе, каждая молекула имеет три степени свободы ее поступательного движения. Но, кроме поступательных, у молекулы могут быть и другие степени свободы: вращательные, колебательные и т. п.

Оказывается, зная функцию распределения молекул по скоростям, можно показать (внимание! это второе главное утверждение заметки), что на любую степень свободы приходится в среднем энергия \(~\frac{1}{2} kT\). (Отсюда и получается коэффициент «\(~\frac{3}{2}\)» в выражении для средней кинетической энергии поступательного движения молекул.) Другими словами, температура — не мера кинетической энергии поступательного движения молекул, а мера энергии, приходящейся на одну любую степень свободы системы.