Kvant. Еще вечный двигатель
Стасенко А.Л. Еще один вечный двигатель? //Квант. — 1998. — № 3. — С. 35-37.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
Первые проекты механического вечного двигателя относятся к 13 веку (Виллар де Оннекур, 1245, Пьер де Марикур, 1269, Франция) …
С 1775 года Парижская Академия наук отказалась рассматривать проекты вечного двигателя.
Физический энциклопедический словарь
Проекты вечных двигателей запрещено рассматривать, чтобы не тратить напрасно время. Но иногда полезно порассуждать и понять, действительно ли некую машину можно отнести к классу запретных «вечных двигателей».
Так вот, один вдумчивый школьник слышал, что молекулы при столкновении со стенкой могут терять определенную часть импульса, а в предельных случаях — отражаться абсолютно упруго (изменяя скорость нормального удара на обратную без изменения модуля) или неупруго (полностью теряя эту скорость и «соскальзывая» уже вдоль поверхности). И тут его осенило.
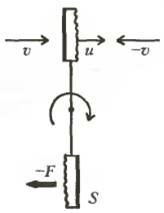
Он решил приобрести пластинку, одна сторона которой отражает молекулы абсолютно упруго, а другая - неупруго, и, вырезав из нее два одинаковых по площади диска, насадить их на стержень (конечно, невесомый), предварительно развернув на 180° их плоскости относительно друг друга, а затем этот стержень укрепить на вертикальной оси, конечно, без трения. И он даже нарисовал это устройство (рис.1, вид сверху). На этом рисунке он обозначил и площадь дисков S, и среднюю тепловую скорость молекул газа υ, и линейную (окружную) скорость дисков u в данное мгновение, а круглой стрелкой показал ожидаемое направление вращения всего устройства. При этом он принял, что левая поверхность верхнего диска отражает молекулы упруго, а правая - неупруго.
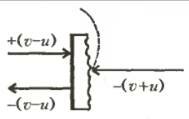
Разумеется, школьник понимал, что молекулы газа движутся равновероятно во всех направлениях, но рисовать их все он не стал, ибо его интересовали только те, которые движутся по направлению к диску или от него. А таких, согласно привычной школьной оценке, в единице объема было \(~\frac n6\) (n - концентрация молекул, «шесть» - это число сторон куба: вверх - вниз, вправо - влево, вперед - назад). Значит, плотность потока молекул (т.е. число молекул, попадающих на единицу площади в единицу времени), догоняющих слева верхний диск, равна \(~\frac n6 (\upsilon - u)\) (легко проверить: при u = υ эти молекулы не догонят диск и не столкнутся с ним). Далее, каждая молекула ударяется о левую поверхность диска со скоростью +(υ - u) (в его системе координат) и, согласно условию упругости удара, отражается обратно с той же по величине скоростью (опять же, в системе диска), но с другим знаком (рис.2): -(υ - u). Значит, в неподвижной (лабораторной) системе координат ее скорость после отражения будет -(υ - u) + u = -υ + 2u, а изменение импульса одной молекулы составит m(-υ + 2u) - mυ. Такой же по величине, но противоположный по знаку импульс получит верхний диск. А умножив его на соответствующую плотность потока молекул и на площадь диска, найдем силу, действующую на верхний диск слева:
Проведем аналогичные рассуждения для правой поверхности верхнего диска. В системе диска скорость перед ударом -(υ + u), а после удара 0. Скорость после удара в лабораторной системе равна u, изменение скорости молекулы в лабораторной системе составляет u - (-υ) = u + υ. Плотность потока молекул, налетающих справа на верхний диск, равна \(~\frac n6 (\upsilon + u)\), так что суммарная сила, действующая на диск справа, будет
Можно далее учесть, что произведение mn равно плотности газа ρ, и записать силу, действующую на верхний диск, в виде
Такая же по величине, но противоположная по направлению сила будет действовать на нижний диск, так что система начнет вращаться под действием пары сил как раз в том направлении, которое указано на рисунке 1.
Ясно, что каждая из сил обратится в ноль (и вращение перестанет ускоряться) при условии
Решая это квадратное уравнение, наш исследователь получил установившуюся линейную скорость:
и, конечно, выбрал отрицательный знак, чтоб не смешить людей - не может ведь диск двигаться быстрее молекул.
Итак, установившаяся окружная скорость дисков \(~u_{\infty} = \upsilon (3 - 2 \sqrt 2) = 0,172 \upsilon\) получилась заметно меньше тепловой скорости молекул, поэтому способный изобретатель догадался пренебречь ее квадратом в выражении для F, так что уравнение, описывающее второй закон Ньютона для диска, приобрело вид следующего линейного дифференциального уравнения относительно u:
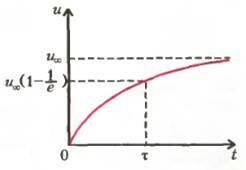
Даже не решая это уравнение, можно кое-что сказать. Из него, в частности, видно, что ускорение с ростом υ уменьшается и обращается в ноль при \(~u_{\infty} = \frac{\upsilon}{6} = 0,167 \upsilon\), что действительно близко к найденному ранее значению. А постоянная величина \(~\tau = \frac{m}{\rho \upsilon S}\) в знаменателе правой части уравнения называется временем релаксации. Например, если взять m = 1 г, ρ = 10-5 кг/м3, υ ~ 300 м/с, S = 1 см2, получится τ ≈ 3·103 с ~ 1 ч. Это — время, за которое почти достигается «предельное значение скорости» \(~u_{\infty}\) (см. рис.3).
Тут надо обратить внимание, что вся теория построена для свободномолекулярного режима обтекания дисков, поэтому наш изобретатель и взял плотность газа на пять порядков ниже, чем для обычного воздуха. Тогда и длина свободного пробега молекул увеличится на пять порядков и, таким образом, вместо 10-7 м станет как раз 1 см, что уже сравнимо с принятым размером диска.
Итак, устройство должно вращаться вечно. К нему даже можно сделать привод и заставить совершать полезную работу. Однако никакого отношения к тому вечному двигателю, который отказывалась рассматривать французская академия, наше устройство не имеет. Оно ведь не пытается родить энергию «из ничего»: диски получают энергию при соударениях молекул со стенками сосуда, которые поддерживаются при постоянной температуре. Так что закон сохранения энергии не нарушается.
Казалось бы, все в порядке, и остается только «изобрести» диски нужной конструкции. Необходимо добиться, чтобы с одной поверхностью молекулы соударялись упруго, а с другой - неупруго. Но оказывается, здесь нашего изобретателя подстерегает немалая опасность. Он очень легко может пойти по ложному пути и увязнуть в тщетных попытках сконструировать нечто столь же невозможное, как и вечный двигатель.
«Зеркальность» упругой поверхности равносильна предположению о ее термодинамическом равновесии с газом: молекулы стартуют с поверхности с такой же средней скоростью, как и падают на нее (температуры газа и поверхности одинаковы). Но как сделать другую поверхность «неупругой»?
Рассмотрим два варианта подхода к решению проблемы. В одном из них (назовем его «механическим») поверхность делают пористой: молекулы, попадающие внутрь цилиндрических пор, ударяются о ее «зеркальные» стенки, а каждая пора, плавно искривляясь под прямым углом, выбрасывает молекулу в конце концов сбоку от пластинки (см. рис. 2).
Другой подход можно назвать «термическим»: специальная жидкость (например, жидкий азот или гелий) постоянно охлаждает «неупругую» поверхность, и средняя энергия отлетающих молекул, определяемая температурой поверхности, будет гораздо меньше, чем энергия падающих молекул.
Какой же из вариантов выбрать? Может показаться, что первый проще и экономичнее: не нужно тратить усилий на поддержание запасов охлаждающей жидкости, а для вращения устройства нужно только поддерживать стенки сосуда при постоянной температуре. Возможно, что такое устройство представляло бы собой нечто замечательное и для человечества весьма полезное. Ведь никто не говорит, какой именно должна быть температура стенок. Можно поместить миллион таких устройств в океан и качать сколько угодно энергии, а потери энергии будут постоянно компенсироваться солнечными лучами. Но люди давно поняли, что подобные устройства - которые могли бы работать за счет энергии одного теплового резервуара — ничем не отличаются от вечного двигателя. Их даже тоже назвали вечными двигателями, но второго рода. На попытки сконструировать такой двигатель было затрачено, неверное, не меньше усилий, чем на создание обычных вечных двигателей (первого рода), - но безуспешно. И это, конечно, неслучайно. На пути изобретателей стоял второй закон (второе начало) термодинамики. Одна из формулировок этого закона гласит: «Невозможен процесс, единственным результатом которого было бы превращение в работу теплоты, взятой из резервуара при постоянной температуре». Или так: «Невозможно существование циклической машины, работающей за счет энергии одного теплового резервуара».[1] Так что «механический» подход к конструированию неупругой поверхности не может быть успешным (кстати - подумайте, почему он не будет работать).
А вот второй, «термический», подход - с использованием охлаждающей жидкости - не противоречит второму закону термодинамики. Ведь кроме «нагревателя» в виде стенок сосуда здесь присутствует и «холодильник» в виде жидкого азота. Но, к сожалению, эффективность такого устройства вряд ли будет высокой.
Итак, ничего вечного и дарового не существует. Хотя, конечно, жаль.
Примечания
- ↑ Затронутая здесь тема (второе начало термодинамики и вечные двигатели второго рода) обсуждаются также в статье «О квантовой природе теплоты». (Прим. ред.)