Kvant. Каустики
Андреев А., Панов А. Каустики на плоскости и в пространстве //Квант. — 2010. — № 3. — С. 48-50
По специальной договоренности с редколлегией и редакцией журнала "Квант"
Каустики - это вездесущие оптические поверхности и кривые, возникающие при отражении и преломлении света. Каустики можно описать как линии или поверхности, вдоль которых концентрируются световые лучи.
Каустики на плоскости (2D каустики)
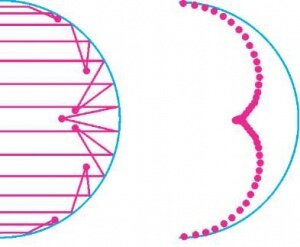
Сначала посмотрим, что происходит, когда все световые лучи и кривая, от которой они отражаются, лежат в одной плоскости. Самый важный пример - это отражение параллельных лучей от окружности. Возникающая здесь каустика - яркая линия с острием, расположенным между вершиной и центром зеркала (рис.1).
Если мы имеем дело с параболой, то все лучи, параллельные ее оси, после отражения собираются в одной точке - фокусе параболы. Для окружности и для других зеркал это не так, отраженные лучи не сходятся в одной точке. Но когда на зеркало падает узкий пучок параллельных лучей, то после отражения он становится сходящимся. Иными словами, отраженный пучок целиком не сходится в одной точке, но узкие пучки, состоящие из близких лучей, будут сходящимися. Точки, в которых они сходятся, это точки концентрации энергии, именно из них и состоит каустика. Эти соображения позволят нам нарисовать каустику.
Запустим на круглое зеркало большое количество параллельных лучей. Разобьем их на пары и отметим точки пересечения лучей в каждой паре после отражения (рис.2). Если число лучей увеличивать, то расстояния между точками попарного пересечения будут уменьшаться. Точки будут располагаться все ближе друг к другу и в пределе заполнят каустическую кривую.
Это один способ понять, как устроена каустика. Другой способ увидеть каустику - это нарисовать много лучей. На полученном таким образом рисунке каустика выделяется как кривая, которой касаются все отраженные лучи (рис.3). Это просто другое проявление той же самой концентрации световой энергии -каждый световой луч касается каустики, значит, проходит вдоль нее значительную часть своего пути и «отдает» ей большую часть своей энергии. Линия, которая касается каждой прямой из некоторого семейства прямых, является огибающей этого семейства. Так что каустика - это огибающая световых лучей. Можно сказать, что каустика представляет собой остов, на который нанизаны все световые лучи.
Как самим можно нарисовать предыдущие картинки?
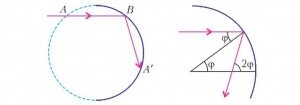
Достроим зеркало до полной окружности (рис.4). Тогда из того, что «угол падения равен углу отражения», следует, что хорды АВ и BA' , высекаемые падающим и отраженным лучами, равны между собой. Так что нужно с помощью циркуля нарисовать окружность с центром в точке В и радиусом АВ и отметить ее пересечение с зеркалом - точку A', а потом по линейке провести отраженный луч BA'. Если для рисования используется компьютер, то тут нужно знать, что горизонтальный (идущий параллельно оси абсцисс) световой луч, отраженный в точке единичной окружности (cos φ, sin φ) с угловой координатой φ , направлен вдоль вектора (- cos 2φ, - sin 2φ). Это позволяет нарисовать все отраженные лучи. А если мы еще хотим добраться от окружности до каустики, то расстояние, которое нужно пройти вдоль этого вектора, равно (cos φ)/2 . Таким образом, точки, лежащие на каустике, будут иметь координаты
Это хорошо известная кривая (ее описывает фиксированная точка окружности, катящейся снаружи по большей в два раза окружности), она имеет собственное имя - нефроида.
Каустики в пространстве (3D каустики)
Все гораздо сложнее и гораздо интереснее в трехмерном пространстве. Там на каждом отраженном луче есть две точки концентрации энергии. В этом смысле можно сказать, что каустическая поверхность в пространстве состоит из двух листов.
В качестве примера возьмем отражающую поверхность вида
и осветим ее сверху пучком, идущим параллельно оси z. Если ограничиться плоскостью y = 0, то мы имеем отражение от параболы z = x2 , а в плоскости x = 0 отражение идет от параболы z = 2y2 . Это разные параболы, и лучи от них сфокусируются на разных высотах, в разных точках оси z. Одна из точек будет лежать на одном листе каустической поверхности, другая - на другом.
В последние годы в Интернете появились фотографии ярких четырехугольных звезд на стенах домов (рис.5). Это результат отражения солнечного света от пластиковых окон из расположенных напротив домов. В пластиковых окнах промежуток между стеклами герметизируется, и оттуда
частично выкачивается воздух. За счет перепада давления стекла деформируются внутрь стеклопакета и приобретают вид, представленный на рисунке 6 (изображение сильно растянуто вдоль вертикальной оси). Такую поверхность можно хорошо приблизить графиком функции подобрав соответствующие постоянные k и m.
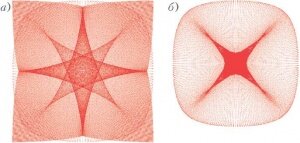
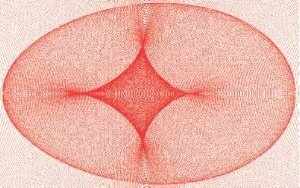
Если ограниченный кусок такой поверхности - «окно» -осветить падающим сверху пучком параллельный лучей, а на пути отраженных лучей поставить экран, то при небольшом удалении от окна мы увидим на экране картину, основным фрагментом которой служит восьмиугольная звезда (рис. 7,а). При большем удалении экрана мы увидим на нем четырехугольную звезду на фоне менее яркого овала (рис.7,6), что соответствует реальным фотографиям. Четыре отсутствующих по сравнению с левым рисунком луча оказались отрезанными от звезды из-за того, что мы рассматриваем отражение только от ограниченного куска поверхности - от квадратного окна.
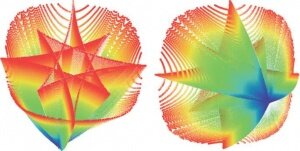
Теперь нарисуем саму каустическую поверхность, соответствующую этой оптической картине. Она на самом деле состоит из двух листов. На рисунке 8 цветом закодировано удаление точек каустики от отражающей поверхности: синие точки находятся ближе к ней, красные - дальше от нее. Сечение одного из листов каустики - восьмиугольная звезда, сечение другого - граница окружающего звезду овала.
Каустики могут образовываться не только при отражении, но и при преломлении света, скажем на поверхности воды. На фотографиях, воспроизведенных на рисунке 9, солнечные лучи преломляются либо на воздушном пузырьке, либо на мениске, возникающем из-за поверхностного натяжения на иголке, погруженной в воду. И тут и там на дне мы видим небольшую четырехугольную звезду.
Смоделируем это явление, задав преломляющую поверхность (рис.10) уравнением
Зафиксируем постоянную k и угол падения солнечных лучей α и вспомним, что для воды показатель преломления n = 1,33. С помощью закона преломления sin α = n sin β можно рассчитать направление преломленных лучей - угол β - и, значит, построить картину, которую формируют лучи на экране, расположенном под поверхностью воды - на дне сосуда. Отчетливо видна та же самая асимметричная четырехугольная звезда (рис. 11), что и на фотографии (см. рис.9)
А вот и соответствующая каустическая поверхность для преломленных лучей (рис.12). Синие точки расположены ближе к поверхности воды, красные более удалены от нее. Сечение внутренней поверхности - четырехугольная звезда, а внешней - граница овала, содержащего эту звезду.
В заключение - наши рекомендации для дальнейшего чтения.
- Об оптических свойствах параболы и других кривых можно прочитать в книге А.Г.Дорфмана «Оптика конических сечений» (Популярные лекции по математике, выпуск 31. - М.: Физматлит, 1950).
- Как записать уравнение огибающей, можно узнать в книге В.Г.Болтянского «Огибающая» (Популярные лекции по математике, выпуск 36. - М.: Физ-матлит, 1961).
- Наконец, об особенностях устройства каустических кривых и каустических поверхностей вы можете прочитать в книге В.И.Арнольда «Теория катастроф» (М.: Наука, 1990).
Смотреть HD
видео онлайн
бесплатно 2022 года