Kvant. Линзы

Зильберман А. Р. Немного о линзах //Квант. — 1993. — № 1. — С. 58-60.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Явление преломления световых лучей на границе раздела прозрачных сред (например, воздух—стекло) можно использовать для самых разных целей в различных оптических приборах. К ним относятся, прежде всего, плоскопараллельные пластины, призмы и линзы.

Чаще всего линзы применяют для получения изображений светящихся (или освещенных) предметов. При помощи линзы можно получить изображение в нужном месте (на пленке фотоаппарата, на экране кинотеатра) или на удобном для рассматривания глазом расстоянии (в лупе, очках, контактных линзах). Можно получить увеличенное во много раз изображение предмета (в микроскопе, в том же кинопроекторе) или уменьшенное (в зрительной трубе или бинокле — да да, именно уменьшенное в несколько десятков или сотен раз, зато приближенное в сотни или тысячи раз, что и позволяет рассмотреть предмет во всех подробностях). А можно получить изображение светящейся точки и в бесконечности — имеется в виду почти параллельный пучок лучей (как, например, в прожекторе).

Во многих практически важных случаях оптическая система содержит несколько линз (так, в объективе фотоаппарата может оказаться более десятка различных линз — собирающих и рассеивающих, совсем тонких и не очень, из разных — специально выбранных — сортов стекла, могут среди них быть линзы с более сложной формой поверхностей, чем привычная сферическая). Нужно сказать сразу, что простейшие расчеты оптических систем, которые можно провести в рамках курса физики для средней школы, довольно плохо подходят для практических расчетов — даже линзы для хороших очков, не говоря уже о контактных линзах, часто рассчитывают на ЭВМ (и вовсе не от избытка этих самых ЭВМ).

Но все же и простая теория может пригодиться — приближенный расчет во многих случаях вполне достаточен.

Рассмотрим ход лучей, падающих на совсем простую линзу — плосковыпуклую, у которой выпуклая поверхность имеет сферическую форму. Такую линзу мы выбрали потому, что расчет хода лучей в ней будет наименее сложным. Пусть линза изготовлена из стекла и находится в воздушной среде.

Представим, что на плоскую поверхность нашей линзы падает параллельный пучок лучей. Известно, что после преломления в собирающей линзе он должен сойтись в точку, лежащую в фокальной плоскости. Покажем это. Для начала сформулируем задачу аккуратнее. Линзу мы будем считать тонкой (по ходу расчетов мы скажем точнее — что такое «тонкая линза» и чем именно приходится пренебрегать), а угол падения лучей — малым (чтобы можно было заменять значения функций sin α и tg α значением самого угла α в радианах, для углов в несколько градусов это дает совсем небольшую ошибку, а расчеты упрощает очень сильно). Условия эти вполне разумны и в общем соответствуют реальному положению для обычных простых оптических экспериментов.

Рис. 1

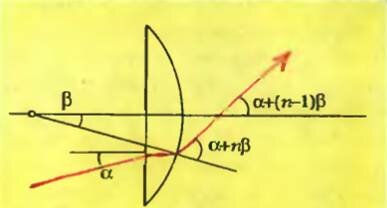
Изобразим линзу и построим ход одного из падающих лучей (рис.1; здесь линза выглядит толстой, а углы большими — это нужно только для наглядности, иначе ничего нельзя было бы разобрать). Выбранный нами луч падает на линзу под углом α к главной оптической оси, после преломления на плоской поверхности угол уменьшится в n раз, где n — показатель преломления стекла. На сферическую границу стекло—воздух луч надает под углом \(~\frac{\alpha}{n} + \beta\) , где β — угол между главной оптической осью линзы и радиусом, проведенном в точку падения луча, а выходит под углом

\(~\left(\frac{\alpha}{n} + \beta \right) n - \beta = \alpha + (n - 1) \beta\) .

Дальше нам понадобится условие тонкости линзы — будем считать, что точки входа луча в линзу и выхода из нее находятся на одинаковых расстояниях от главной оптической оси, равных Rβ. Если теперь отойти от линзы вправо на расстояние L, то в этом месте луч будет сдвинут по вертикали относительно точки выхода из линзы на \(~L(\alpha + (n - 1) \beta)\), и расстояние до главной оптической оси составит

\(~H = L(\alpha + (n - 1) \beta) - R\beta\) .

Рис. 2

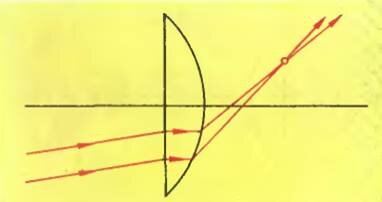
Два различных луча из падающего пучка пересекаются справа от линзы в некоторой точке (рис.2). Приравняем расстояния Н для двух лучей и найдем расстояние L до точки пересечения:

\(~L(\alpha + (n - 1) \beta_1) - R\beta_1 = L(\alpha + (n - 1) \beta_2) - R\beta_2\) ,

откуда

\(~L = \frac{R}{n - 1}\) .

Мы видим, что полученное расстояние не зависит от угла β, т.е. одинаково для всех лучей из нашего пучка. Значит, мы доказали, что пучок после преломления сойдется в точку, и нашли расстояние от линзы до этой точки. Заметим, что при различных углах падения пучка на линзу все точки пересечения лежат в плоскости, которая перпендикулярна главной оптической оси линзы и находится на расстоянии \(~\frac{R}{n - 1}\) от линзы. Иными словами, мы вычислили фокусное расстояние для нашей линзы\[~F = \frac{R}{n - 1}\].

Совершенно таким же образом (только после более длинных вычислений) можно получить аналогичную формулу для фокусного расстояния линзы, которая ограничена двумя сферическими поверхностями радиусов R₁ и R₂. Ее удобно записать в несколько ином виде:

\(~\frac 1F = (n - 1) \left(\frac{1}{R_1} + \frac{1}{R_2} \right)\) .

Радиусы могут быть оба положительными — для двояковыпуклой линзы, оба отрицательными — для линзы, вогнутой с двух сторон, разных знаков — для выпукло-вогнутой линзы (а в нашем случае плосковыпуклой линзы один из радиусов оказывается бесконечно большим). При этом, если фокусное расстояние линзы оказывается положительным (фокус линзы — действительный), т.е. параллельные лучи после преломления действительно сходятся в точке, такую линзу называют собирающей (или положительной) . Если же фокусное расстояние отрицательное (фокус мнимый), т.е. параллельные лучи после преломления расходятся, линзу называют рассеивающей (или отрицательной).

Существует простое соотношение, называемое формулой линзы (его можно получить геометрически) , которое связывает между собой расстояние d от предмета до линзы, расстояние f от линзы до изображения предмета и фокусное расстояние линзы F:

\(~\frac 1d + \frac 1f = \frac 1F \) .

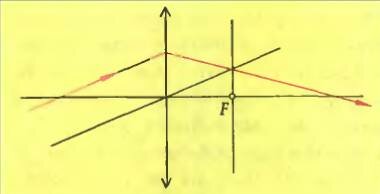
Итак, параллельный пучок лучей после преломления в собирающей линзе сходится в точке, находящейся в фокальной плоскости. Это позволяет легко построить ход произвольного луча после преломления. Для этого достаточно нарисовать параллельно ему вспомогательный луч, проходящий через оптический центр линзы (этот луч не преломляется), и найти точку пересечения этого луча с фокальной плоскостью — через эту же точку должен пройти и основной луч после преломления (рис.3). Возможность построения хода произвольного луча очень помогает, когда нужно строить изображение в сложной оптической системе, содержащей несколько линз, — при этом нет необходимости получать промежуточные изображения после каждой линзы.

Рис. 3

Важно отметить, что при таком способе построения хода лучей можно выбирать любые лучи, даже идущие под большими углами к главной оптической оси линзы, — причем при необходимости можно увеличить диаметр линзы, чтобы лучи на нее попали. Дело в том, что метод построения соответствует «бумажной» линзе — не линзе, а формуле линзы. Для настоящей линзы такой результат получится лишь для «правильных» лучей, идущих под малыми углами к главной оптической оси — а именно это нам и нужно.

Рис. 4

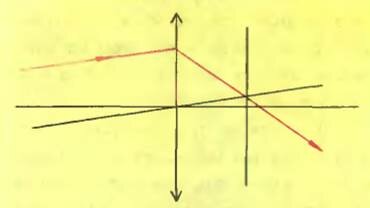
Воспользуемся этим методом для решения несложной задачи. На рисунке 4 изображены собирающая линза и ее главная оптическая ось и задан ход одного луча до и после преломления в линзе. Нужно найти положение фокальной плоскости. Проведем вспомогательный луч параллельно падающему так, чтобы он проходил через центр линзы,— этот луч не преломляется, а точка его пересечения с преломленным лучом как раз лежит в фокальной плоскости линзы. Кстати, можно «обратить» лучи — считать преломленный луч падающим, а бывший падающий — преломленным и, как и в первом случае, построить фокальную плоскость с другой стороны линзы. Впрочем, обе фокальные плоскости должны быть на одинаковом расстоянии от центра линзы.

Рис. 5

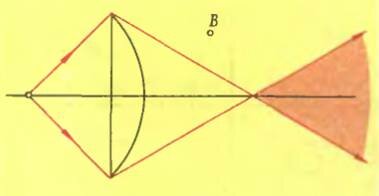
Вернемся к «настоящим» линзам. Обычно считается, что точечный источник света испускает лучи равномерно во все стороны. Где бы ни был расположен глаз, в него попадет расходящийся пучок лучей и мы увидим светящуюся точку. Совсем другое дело, когда мы хотим увидеть изображение этой точки в линзе. Будем считать, что на рисунке 5 изображена «настоящая» линза и задан ее размер. В этом случае изображение точечного источника в линзе образовано пучком лучей, крайние лучи которого ограничены диаметром линзы. Соответственно, этими крайними лучами ограничен и пучок на выходе линзы. Изображение можно увидеть, только находясь в телесном угле, образованном лучами, прошедшими точку пересечения после линзы. Любопытно, что есть такие точки, откуда не виден ни источник, ни его изображение в линзе. Например, точка В — источник закрыт линзой, а в телесный угол, из которого видно изображение, мы не попали. Для того чтобы расширить область, из которой можно видеть действительное изображение, можно использовать экран. Если поместить экран в место пересечения лучей после преломления их в линзе, то от изображения на экране лучи будут распространяться во все стороны (диффузное отражение). Так и делают в кинотеатре. Если же попробовать смотреть фильм, сидя лицом к объективу киноаппарата или поместив на место экрана зеркало, то мы в лучшем случае увидим маленький фрагмент общей картинки, причем из разных мест будут видны разные фрагменты.