Kvant. Парадоксы м. поля
Кузьмин П. Парадоксы постоянного магнитного поля //Квант. — 1995. — № 3. — С. 36-37.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
Когда съедают бублик, куда девается дырка?
Загадка
Конечно же, вы знаете о том, что магнитное поле — это то, что возникает вокруг проводника с током и способно притягивать другой проводник, если по нему тоже течет ток, или отталкивать его, или вообще двигать куда-то в сторону (смотря по тому, как этот второй проводник и его ток направлены). А почему, собственно, проводники с постоянным током вдруг начинают действовать друг на друга? Согласитесь, есть что-то не совсем понятное в этих магнитных силах.
Посмотрите, как просто выглядят закон всемирного тяготения и закон Кулона и как похожи друг на друга формулы этих законов! Силы гравитационного и электростатического взаимодействий направлены по прямой, соединяющей массы или заряды, а величины сил в обоих случаях обратно пропорциональны квадратам расстоянии. Правда, есть и различия — заряды могут не только притягиваться, но и отталкиваться. А самое главное сходство в том, что эти силы связывают между собой материальные объекты — носители массы или заряда.
Совсем другое дело с магнитным полем. Здесь взаимодействуют токи. А что такое токи? Всего лишь движения зарядов в одном направлении. Получается, что взаимодействуют как бы движения, а не тела. Правила этих взаимодействий — выражение для силы Ампера плюс правило левой руки — тоже никак не похожи на законы электростатики и гравитации. И совсем уж странные вещи начинаются, если копнуть чуть глубже.
Вот — два примера.
1)
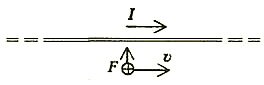
Представим себе длинный прямой проводник, по которому течет ток I (рис.1). Пусть этот проводник электростатически нейтрален, и пусть вдоль него движется заряженная частица. Поскольку эта частица движется направленно и, значит, является сама по себе электрическим током, на нее со стороны проводника действует магнитная сила, которая притягивает частицу к проводнику или отталкивает ее — в зависимости от направлений тока и движения частицы. Если частица двигалась по инерции, то ее траектория, конечно, искривится в сторону проводника или от него, что можно наблюдать в опытах. Как будто бы все просто и понятно.
А теперь представим себе, что мы не сидим и смотрим на все это, а движемся в маленьком вагоне вдоль проводника с током, причем со скоростью и, как у нашей заряженной частицы. Как говорят в таких случаях, перейдем в другую систему координат. Частица теперь для нас неподвижна, она больше не ток. Значит, магнитные силы на нее не действуют? А куда же они делись? Ведь не может же быть, что в одной системе координат проводник притягивает частицу, а в другой — нет. Должно же меняться расстояние между проводником и частицей, как вначале.
Заметим, однако, что теперь мимо нас, сидящих в воображаемом вагоне, движется проводник с током. Это и поможет нам разобраться в ситуации. Правда, придется воспользоваться одним из законов теории относительности, который состоит в том, что с точки зрения неподвижного наблюдателя в любом движущемся объекте сокращаются все линейные размеры в направлении движения. При скоростях, близких к скорости света, эти сокращения могут быть заметны «на глаз», а при обычных скоростях электронов в проводниках (это доли миллиметра в секунду) эффекты сокращений очень-очень малы, но именно они все и объясняют в нашем случае.
В исходной ситуации, когда проводник с током мы считали неподвижным, на самом деле была неподвижна только его кристаллическая решетка, а электроны проводимости, которые и обусловливают ток в обычных проводниках, двигались все в одном направлении, создавая ток. Теперь попробуем двигаться вместе с электронами, так чтобы они в нашей новой системе координат стали неподвижными. Для определенности будем считать, что скорость нашей новой системы координат, т.е. скорость движения электронов, равна исходной скорости υ движения заряженной частицы. Кристаллическая решетка в этой системе координат движется, создавая ток. Что изменилось? Положительно заряженные ядра атомов в кристаллической решетке теперь для нас направленно движутся, и, следовательно, расстояния между ними чуть-чуть меньше исходных Это означает, что плотность положительных зарядов увеличилась. Электроны, наоборот, двигаться направленно перестали, значит, пропал эффект сокращения расстояний и их плотность уменьшилась. Таким образом, в движущейся системе координат проводник стал положительно заряженным! И в точке, где находится заряженная частица, он должен создавать электрическое поле. Самое интересное во всем этом то, что возникшие электростатические силы, если произвести все расчеты, оказываются в точности равными тем магнитным силам, которые мы, чуть было, не потеряли. (Тех, кто заинтересовался расчетом, мы отсылаем к замечательной книге «Фейнмановские лекции по физике» (т. 5, с.266), выпущенной издательством «Мир» в 1966 г. — Прим.ред.) Они-то теперь и действуют на нашу заряженную частицу. Как ни малы эффекты сокращения расстояний, но электронов в металле очень много, и их суммарный заряд как раз подходит для того, чтоб все сошлось.
Удивительное превращение! Получается, что электрическое и магнитное поля не существуют отдельно, а для разных наблюдателей одно и то же поле может проявляться как магнитное или как электрическое или как их смесь в самых разных пропорциях.
2)
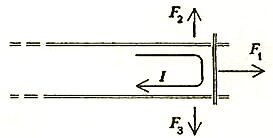
Пусть есть два очень длинных проводника (рис.2), к которым где-то далеко слева подключен источник тока плюсом к одному проводнику, а минусом — к другому. И пусть на этих проводниках перпендикулярно им лежит перемычка — неважно, скользящая без трения или закрепленная, поскольку мы будем рассматривать только магнитные силы. Ток течет по верхнему проводнику вправо до перемычки, по перемычке вниз и от перемычки по нижнему проводнику влево. Как направлена магнитная сила, действующая на перемычку? Как направлены магнитные силы, действующие со стороны перемычки на параллельные проводники?
Для ответа на эти вопросы воспользуемся правилом буравчика, законом Ампера и правилом левой руки. Из них найдем, что ток, текущий по длинным проводникам, создает около перемычки магнитное поле, направленное от читателя за рисунок, значит, на перемычку действует сила, направленная вправо. Перемычка создает около длинных проводников магнитное поле, направленное в ту же сторону, следовательно, на верхний проводник со стороны перемычки действует магнитная сила, направленная вверх, а на нижний — вниз.
А как же третий закон Ньютона? Сила, с которой Земля притягивает к себе яблоко, равна силе, с которой яблоко притягивает Землю. И неважно, висит это яблоко на дереве или летит в космическом пространстве. А у нас что получилось? Длинные проводники пытаются толкать перемычку вправо, а перемычка действует на них магнитными силами, сумма которых вообще равна нулю. Как же так?
Можно сообразить, что поскольку электрическая цепь замкнута, то где-то далеко слева есть еще одна перемычка, на которую действует магнитная сила, как раз противоположная той, что приложена к нашей перемычке, и сумма всех магнитных сил, действующих на цепь в целом, благополучно равна нулю.
(Точно так же, если рассмотреть два контура с током, то взаимодействие отдельных элементов может не подчиняться третьему закону Ньютона, но суммарная сила взаимодействия контуров ему подчиняется. А так как токи всегда замкнуты, то все в порядке. — Прим. ред.)
Смотреть HD
видео онлайн
бесплатно 2022 года