Kvant. Парадокс Вавилова

Фабрикант В.А. Парадокс Вавилова //Квант. — 1995. — № 1. — С. 39-40.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

В геометрической оптике часто и плодотворно применяется понятие о пучке параллельных световых лучей, имеющем конечное поперечное сечение. Более того, даже в теории такого волнового явления, как интерференция, во многих случаях допустимо использование этого понятия.

Во многих случаях, ио далеко не во всех. В книге «Микроструктура света» известного советского физика С.И.Вавилова разобран весьма поучительный в этом смысле оптический парадокс.

Напомним коротко, как выглядит энергетика интерференционной картины. Интерференция, как мы знаем, есть сложение колебаний. В нашем случае в волнах колеблются значения напряженности электрического и индукции магнитного полей. Эти величины в каждой точке пространства в каждый момент времени определяют энергию электромагнитного поля. Электромагнитная волна переносит энергию, и можно ввести понятие о плотности потока энергии. Так мы называем величину, равную энергии поля, протекающей в единицу времени через единицу поверхности.

Каждая волна характеризуется еще и фазой. Если при сложении двух световых пучков разность их фаз остается все время одной и той же, мы говорим, что имеем дело с когерентными пучками.

В интерференционной картине, возникающей в результате сложения двух когерентных пучков, происходит пространственное перераспределение световой энергии. В светлых полосах энергия больше, чем сумма энергий складываемых пучков; в темных полосах она, наоборот, меньше. Избыток энергии в светлых полосах как раз компенсируется недостатком ее в темных. Полная энергия, распределенная по всей интерференционной картине, точно равна сумме энергий двух интерферирующих пучков.

Рис. 1

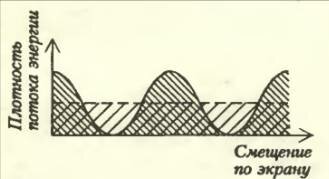
На рисунке 1 показана зависимость плотности потока энергии в интерференционной картине от смещения по экрану, на котором она наблюдается. Картина получена при сложении двух когерентных световых пучков равной энергии. Горизонтальная пунктирная линия изображает сумму плотностей потоков энергий в складываемых пучках. Части кривой, идущие над этой прямой, соответствуют светлым интерференционным полосам, а части кривой, лежащие под пунктирной прямой, — темным. Суммарная энергия, распределенная в интерференционной картине, изображается площадью под кривой. Эта площадь точно равна площади под пунктирной прямой. Требования строгого бухгалтера природы — закона сохранения энергии — выполняются неукоснительно.

Рис. 2

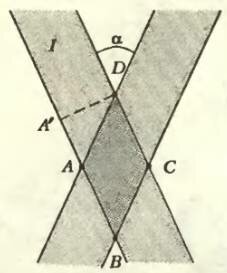
Перейдем теперь к парадоксу Вавилова. Представьте два совершенно одинаковых когерентных резко ограниченных световых пучка шириной а, пересекающихся под малым углом α (рис.2). В области ABCD происходит интерференция. Для наблюдения интерференционной картины можно установить экран, перпендикулярный плоскости чертежа, проходящий через точки A и C. Интерференционная картина будет состоять из прямолинейных чередующихся светлых и темных полос, заполняющих экран от точки A до точки C (рис.3).

Рис. 3

Распределение плотности потока энергии в интерференционной картине соответствует графику на рисунке 1. Если у обоих пучков одинаковые начальные фазы световых колебаний, то разность фаз световых волн первого и второго пучков в точках, лежащих на прямой BD будет равна нулю. Она соответствует, таким образом, середине центральной светлой полосы. В середине соседней, темной полосы разность фаз должна быть равна π, иными словами, световые колебания в обоих пучках должны быть в противофазе. Разность фаз Δφ равна разности хода ΔL обеих волн до данного места, деленной на длину волны и умноженной на 2π:

\(~\Delta \varphi = 2 \pi \frac{\Delta L}{\lambda}\) . (1)

Увеличению длины пути, проходимого волной, на λ соответствует запаздывание фазы на 2π. Из формулы (1) следует, что в середине ближайшей к центру интерференционной картины темной полосы ΔL должно быть равно λ / 2.

Подсчитаем разность хода в точке А. Параллельный пучок можно рассматривать как поток плоских волн, перпендикулярных направлению световых лучей. Проведем через точку D (см. рис.2) одну из волновых поверхностей (поверхностей равной фазы) первого пучка. На этой волновой поверхности лежат точки D и А’. Пути, проходимые обоими пучками до точки D, одинаковы. Для того чтобы попасть в точку А, волновая поверхность первого пучка, проходившая ранее через точку D, должна сместиться на отрезок А’А, а волновая поверхность второго пучка, проходившая ранее также через точку D, должна сместиться на отрезок DA. В результате возникает разность хода

\(~\Delta L = DA - A'A = a \left( \frac{1}{\sin \alpha} - \frac{1}{\operatorname{tg} \alpha}\right) = \frac{2a \sin^2 \frac{\alpha}{2}}{\sin \alpha} = a \operatorname{tg} \frac{\alpha}{2}\) . (2)

Ясно, что такая же разность хода, но с обратным знаком будет в точке С. Начнем теперь уменьшать угол α. При достаточно малом α можно сделать ΔL равным λ /4. Тогда вся область AC будет заполнена одной светлой интерференционной полосой. Следовательно, всюду энергия будет превышать сумму энергий двух пересекающихся пучков. Никакой компенсации за счет образования темных полос нет, так как они вообще отсутствуют!

Можно получить и, так сказать, негативный результат, заставив пересекаться пучки с начальной разностью фаз, равной π. Тогда область AC будет заполнена темной интерференционной полосой.

В первом случае непонятно, откуда берется дополнительная энергия, во втором — неясно, куда исчезает энергия.

Оба случая явно противоречат закону сохранения энергии. Очевидно, в наших рассуждениях есть какой-то дефект, приводящий к противоречию с одним из основных законов природы. Чтобы понять, в чем здесь дело, запишем формулу (2) для указанного случая, когда \(~\Delta L = \frac{\lambda}{4}\), и воспользуемся при этом малостью угла α (tg α ≈ α для малых α). Тогда получим

\(~\frac{\lambda}{4} = \frac{a \alpha}{2}\), или \(~\alpha = \frac 12 \frac{\lambda}{a}\) . (3)

Покажем, что угол α действительно должен быть малым. Возьмем а = 1 см, λ = 5·10^-5 см, тогда α = 2,5·10^-5 радиана Мы видим, что неприятности с законом сохранения энергии возникают при угле между пучками порядка отношения длины волны к величине поперечного сечения пучка.

Решение парадокса заключается в том, что при таких малых углах уже нельзя пользоваться понятием идеального параллельного пучка конечного сечения. При любой попытке реализовать такие пучки мы потерпим неудачу. Ограничение размеров пучка благодаря явлению дифракции с необходимостью приводит к превращению его в расходящийся пучок. Угол расхождения пучка определяется как раз формулой (3). При этом, естественно, угол, под которым пересекаются пучки, можно определить лишь с точностью до величины порядка угла расхождения пересекающихся пучков.

Если бы дифракция еще не была открыта, мы на основании закона сохранения энергии и формулы (3) должны были бы не только догадаться о ее существовании, но и указать на основную закономерность, управляющую величиной дифракционного угла. Это хороший пример того, что закон сохранения в физике всегда может служить надежной путеводной звездой.

Взяв реальные световые пучки, мы никогда, конечно, не получим противоречия с законом сохранения энергии. В интерференционных опытах данного типа всегда дело будет сводиться к пространственному перераспределению потока энергии.

Есть, однако, интерференционные эксперименты, где возникают еще более тонкие энергетические парадоксы, но это, как говорится, уже другая история.