Kvant. Преобразование эл. цепей
Зильберман А.Р. Преобразование электрических цепей //Квант. — 2002. — № 3. — С. 30-31,34.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
В этой статье рассказывается о методе, позволяющем упрощать сложные задачи по расчету электрических цепей.
Что мы понимаем под «преобразованием цепи»? Предположим, что у нас есть сложная схема из резисторов, имеющая множество выводов и подключенная к источникам. Заменим эту схему другой, но с тем же числом выводов, причем так, чтобы сопротивления между двумя любыми выводами у новой схемы были такими же, как у старой. Ясно, что источники «ничего не узнают» об этой замене и токи, потребляемые схемой, останутся прежними. Но найти эти токи, возможно, окажется проще.
Итак, если мы хотим подсчитать токи в сложной схеме, ее можно заменить более простой эквивалентной схемой. При этом токи внутри заменяемой части меняются. Поэтому так поступать можно только с той частью схемы, которая нас непосредственно не интересует.
С подобными заменами вы, конечно же, встречались. Пусть, например, в схеме два сопротивления[1] r1 и r2 включены последовательно. Их мы можем заменить одним, равным по величине сумме r1 + r2. Если же два сопротивления включены параллельно, то их также можно заменить одним, величина которого равна \(~\frac{r_1 r_2}{r_1 + r_2}\) . Это — простейшие примеры преобразования цепей. Мы же остановимся на более сложных схемах.
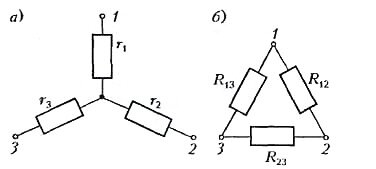
Посмотрим, как преобразуются друг в друга схемы, имеющие по три вывода, - «звезда» и «треугольник» (рис.1).
Немного непривычные обозначения на рисунке 1,б очень удобны — индексы показывают, между какими точками включено сопротивление. Например, сопротивление R13 включено между точками 1 и 3 и т.д.
Если мы хотим заменить одну из этих схем другой, нужно получить такие соотношения между r и R, чтобы сопротивления между любыми точками были для обеих схем одинаковы.
В схеме «звезда» (см. рис. 1, а) сопротивление между точками 1 и 2 равно r1 + r2, а в схеме «треугольник» оно равно \(~\frac{R_{12} (R_{13} + R_{23})}{R_{12} + R_{13} + R_{23}}\) . Следовательно, для того чтобы со- противления между точками 1 и 2 были одинаковы для обеих схем, необходимо, чтобы
Аналогично, для точек 2 и 3
и для точек 1 и 3:
Система уравнений (1) — (3) легко решается. Сложим все уравнения и поделим обе части на 2:
Вычтя теперь из этого уравнения уравнение (2), получим
Аналогично,
и
Эти результаты легко запомнить - знаменатель всюду один и тот же, а в числителе справа дважды встречается тот же индекс, что и слева\[~r_1 \to R_{12} R_{13}, r_2 \to R_{12} R_{23}, r_3 \to R_{13} R_{23}\] .
Немного сложнее получить формулы для обратного преобразования:
но их также легко запомнить - числитель всюду один и тот же, а в знаменателе стоит как раз тот индекс, которого недостает слева.
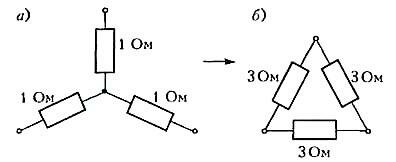
Пользуясь формулами, которые мы только что получили, можно производить замену одной схемы другой. Например, «звезду» с сопротивлениями 1 Ом можно заменить «треугольником» с сопротивлениями 3 Ом (рис.2).
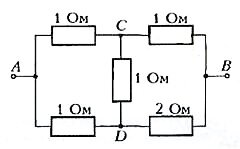
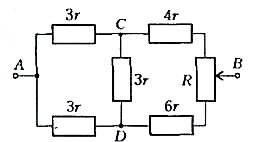
Решим теперь такую задачу: найдем сопротивление между точками A и B в схеме на рисунке 3.
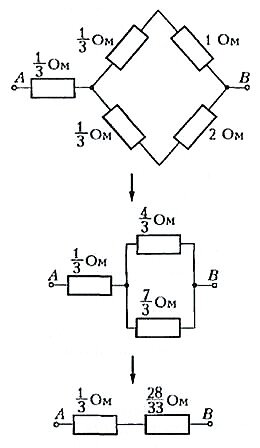
Это обычная схема «мостика», но в нашей задаче «мостик» неуравновешен. Такие задачи приходится решать при помощи правил Кирхгофа. В школьной программе их нет, да и вычисления с помощью этих правил очень громоздкие - в нашем случае получилась бы система пяти уравнений с пятью неизвестными. Мы поступим проще: заменим «треугольник» ACD «звездой», как показано на рисунке 4.
Теперь ясно, что сопротивление между точками A и B будет равно
Мы заменяли «треугольник» ACD «звездой», но можно было решать задачу иначе - заменяя «звезду» ADB «треугольником» (проделайте зто самостоятельно).
Пусть теперь к точкам A и B подключена батарея с пренебрежимо малым внутренним сопротивлением и ЭДС ε = 1 В. Нужно найти ток через участок СВ. Понятно, что преобразовать схему надо так, чтобы не затронуть интересующее нас сопротивление СВ. Подойдет то преобразование, которое мы делали раньше (см. рис.4). Используя, что \(~R_{AB} = \frac{13}{11}\) Ом , получим
После разветвления токи в верхней и в нижней ветвях поделятся в отношении, обратном сопротивлениям ветвей:
Отсюда находим
Немного сложнее было бы найти ток, идущий через участок CD. Для этого пришлось бы еще найти ток через участок АС, а затем вычесть из него найденный уже ток через участок СВ.
Можно еще немного усложнить задачу — учесть внутреннее сопротивление батареи r. Тогда полный ток равен
а остальные токи находятся так же, как и раньше.
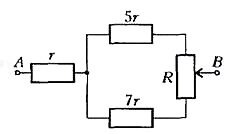
Рассмотрим более интересную задачу, найдем, при каком соотношении между величинами r и R сопротивление между точками А и В в схеме, показанной на рисунке 5, максимально в крайнем положении движка потенциометра.
Сначала преобразуем схему, заменив «треугольник» ACD «звездой» (рис.6). Очевидно, что сопротивление r не влияет на соотношение сопротивлений в остальной цепи. Займемся поэтому оставшейся частью схемы. Тут включены параллельно два сопротивления: 5r + R1 и 7r + R2, где R1 и R2 - сопротивления верхней и нижней частей потенциометра соответственно. При этом сумма сопротивлений 5r + R1, и 7r + R2 остается постоянной. Посмотрим, какими они должны быть, чтобы полное сопротивление было максимальным. Обозначим
Тогда общее сопротивление включенных параллельно частей схемы равно
Если учесть, что
то
Это выражение максимально, когда максимален числитель. Но \(~y = cr_1 - r^2_1\) - это уравнение параболы, ветви которой пересекают ось абсцисс в точках 0 и с. Поэтому числитель дроби наибольший при \(~r_1 = \frac c2\). Так как r1 + r2 = с, то это означает, что сопротивление между точками А и В максимально, если r1 = r2, т.е.
Ясно, что это возможно лишь в том случае, если сопротивление всего потенциометра R = R1 + R2 не меньше чем 2r. В противном же случае максимум сопротивления между точками A и B достигается, когда движок потенциометра находится в крайнем положении.
Итак, ответ: R ≤ 2r.
Метод, о котором мы рассказали, очень удобен для последовательного преобразования сложной схемы к простому виду. Он позволяет рассчитать практически любую сложную цепь, состоящую из сопротивлений. Однако его можно применять и к цепям, содержащим не только сопротивления. Обратим внимание на то, что мы вообще не говорили нигде о физических процессах в цепи, а пользовались только формальным выражением для закона Ома: U = rI. Из него следует, что при последовательном соединении сопротивлений их величины складываются, а при параллельном - складываются величины, обратные сопротивлениям. Понятно, что если какие-нибудь другие физические величины связаны законом, аналогичным закону Ома, то все наши выводы справедливы и для них.
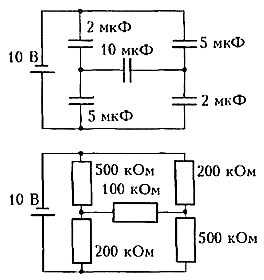
В качестве примера рассмотрим цепь с конденсатором (рис.7). Мы знаем, что заряд конденсатора Q связан с его емкостью C и напряжением на нем U соотношением
Сравним последнее выражение с выражением для закона Ома U = rI. Видно, что законы похожи, только вместо тока стоит заряд, а вместо сопротивления-величина, обратная емкости. Это означает, что для того чтобы найти, скажем, заряды на конденсаторах, можно поступить так: вместо цепи, содержащей конденсаторы, нарисовать цепь, содержащую сопротивления, причем конденсатор емкостью C(Ф) заменить сопротивлением \(~r = \frac 1C\) (Ом). После того как мы рассчитаем токи в цепи из сопротивлений, можно сразу записать, каковы заряды на конденсаторах: если по сопротивлению течет ток I = х (А), то на соответствующем конденсаторе будет заряд Q = х (Кл). ЭДС батарей при таком преобразовании цепи остаются без изменения. Но, разумеется, в цепи с конденсаторами внутренние сопротивления батарей не влияют на результат. Поэтому, преобразуя цепь, нам придется лишить батареи их внутренних сопротивлений.
Пусть, например, нужно найти заряд на конденсаторе емкостью 10 мкФ в схеме, изображенной на рисунке 8. Конденсатору емкостью С = 2 мкФ = 2·10-6 Ф соответствует сопротивление r = 5·105 Ом = 500 кОм. Далее расчет проводится уже достаточно просто (проделайте это самостоятельно).
Таким образом, метод преобразования цепей, как мы видим, пригоден и для схем из конденсаторов.
Примечания
- ↑ Здесь и далее более правильно говорить «два резистора с сопротивлениями r1 и r2» (Прим. ред.)
Смотреть HD
видео онлайн
бесплатно 2022 года