Kvant. Сила Ампера

Лузин А. Сила Ампера в однородном магнитном поле //Квант. — 1991. — № 5. — С. 39,42-43.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Согласно закону Ампера, выражение для модуля силы \(~\vec F\), действующей на малый отрезок проводника Δl, по которому течет ток I, в магнитном поле с индукцией \(~\vec B\), имеет вид

\(~F = BI \Delta l \sin \alpha\) .

Здесь α — угол между направлением магнитной индукции и направлением тока. Можно сказать также, что это угол между вектором \(~\vec B\) и вектором \(~\vec {\Delta l}\), направленным по току. Сила \(~\vec F\) направлена перпендикулярно векторам \(~\vec B\) и \(~\vec {\Delta l}\) — по известному правилу левой руки.

Чтобы найти силу, действующую на криволинейный участок проводника в произвольном магнитном поле, нужно:

а) разбить его на отрезки, настолько малые, что их можно считать прямолинейными, а поле в этой области однородным;

б) определить силы Ампера, действующие на каждый такой отрезок;

в) вычислить векторную сумму полученных сил.

Разумеется этот «рецепт» известен каждому, кто изучал закон Ампера по школьному учебнику физики. Наша же задача — познакомить вас с весьма полезными свойствами силы Ампера, действующей на криволинейный участок проводника с током в простейшем магнитном поле — однородном.

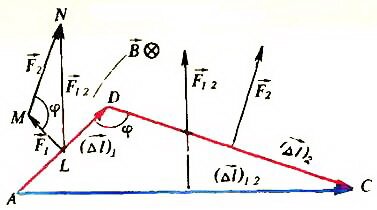
Пусть проводник представляет собой пространственную (в частном случае плоскую) ломаную линию, состоящую из N прямолинейных отрезков (Δl)₁, (Δl)₂, …, (Δl)₃. Просуммируем сначала силы \(~\vec F_1\) и \(~\vec F_2\), действующие на отрезки проводника (Δl)₁ и (Δl)₂.

Рис. 1

Предположим, что вектор \(~\vec B\) перпендикулярен плоскости выбранных отрезков (рис. 1). Сила \(~\vec F_1\) перпендикулярна вектору \(~(\vec {\Delta l})_1\), а ее направление определяется правилом левой руки. Точно так же сила \(~\vec F_2\) перпендикулярна вектору \(~(\vec {\Delta l})_2\). Модули этих сил равны соответственно

\(~F_1 = BI (\Delta l)_1\) и \(~F_2 = BI (\Delta l)_2\) .

Сложим попарно силы \(~\vec F_1\) и \(~\vec F_2\) и отрезки \(~(\vec {\Delta l})_1\) и \(~(\vec {\Delta l})_2\). Поскольку ∠LMN = ∠ADC, как углы со взаимно перпендикулярными сторонами, треугольники LMN и ADC подобны, а вектор \(~\vec F_{12} = \vec F_1 + \vec F_2\) перпендикулярен вектору \(~(\vec {\Delta l})_{12}\), причем \(~F_{12} = BI (\Delta l)_{12}\). Следовательно, сила Ампера, действующая на участок проводника ADC, представляющий собой две стороны треугольника, равна силе Ампера, действующей на прямой отрезок проводника (Δl)₁₂ (третью сторону АС того же треугольника), если и в том и в другом проводнике текут одинаковые токи.

Рис. 2

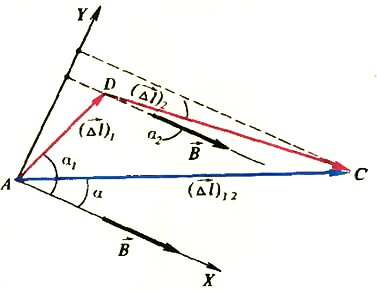
Рассмотрим теперь другой, тоже простой случай, когда вектор \(~\vec B\) лежит в плоскости отрезков проводника (Δl)₁ и (Δl)₂ (рис. 2). Направим ось координат X вдоль вектора \(~\vec B\), а ось Y — перпендикулярно ему. Силы \(~\vec F_1\) и \(~\vec F_2\) направлены от нас перпендикулярно плоскости рисунка — в соответствии с правилом левой руки. Суммарная сила \(~\vec F_{12}\) направлена так же, а ее модуль равен

\(~F_{12} = F_1 + F_2 = BI (\Delta l)_1 \sin \alpha_1 + BI (\Delta l)_2 \sin \alpha_2 = BI (\Delta l)_{12y} = BI (\Delta l)_{12} \sin \alpha\) .

Здесь мы воспользовались тем, что сумма проекций на ось Y векторов \(~(\vec {\Delta l})_1\) и \(~(\vec {\Delta l})_2\) равна проекции суммарного вектора \(~(\vec {\Delta l})_{12}\).

Таким образом, в обоих рассмотренных нами случаях при вычислении силы Ампера два соседних прямолинейных отрезка проводника можно заменить одним, начало которого находится в начале первого отрезка, а конец — в конце второго.

Когда вектор \(~\vec B\) направлен под произвольным углом к плоскости отрезков проводника (Δl)₁ и (Δl)₂, его можно разложить на два взаимно перпендикулярных вектора, один из которых перпендикулярен упомянутой плоскости, а другой лежит в ней. Отсюда, а также из принципа суперпозиции магнитных полей следует, что и при вычислении силы Ампера, действующей на проводник в произвольно ориентированном магнитном поле, два соседних прямолинейных отрезка проводника (Δl)₁ и (Δl)₂ можно заменить одним (Δl)₁₂, соединяющим начало первого и конец второго. Точно так же два прямолинейных отрезка (Δl)₁₂ и (Δl)₃ можно заменить отрезком (Δl)₁₂₃. Продолжая замены, легко увидеть, что сила Ампера, действующая на рассматриваемый нами «ломаный» проводник, равна силе Ампера, действующей на прямолинейный проводник, если в проводниках текут одинаковые токи, а их концы совпадают. Это же справедливо и для криволинейного проводника, так как, неограниченно уменьшая длины прямолинейных отрезков (\(~\Delta l \to 0\)) и одновременно неограниченно увеличивая их число (\(~N \to \infty\)), ломаную линию можно превратить в гладкую (без изломов) кривую.

А теперь — об обещанных свойствах силы Ампера. Из всего сказанного следует, что сила Ампера, действующая на криволинейный участок проводника с током в однородном магнитном поле, не зависит от формы проводника, а зависит только от координат начала и конца этого участка. Следует также и то, что сила Ампера, действующая на замкнутый проводник с током в однородном магнитном поле, равна нулю. Эти два свойства силы Ампера взаимосвязаны — из первого следует второе и наоборот.