Kvant. Хочешь общаться - излучай
Стасенко А.Л. Хочешь общаться - излучай //Квант. — 2000. — № 5. — С. 37-38.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
Возможность воздействия одного тела на другое на расстоянии через пустоту без посредства чего-нибудь еще...
- для меня это настолько бессмысленно, что, по-моему, к такому заключению никогда не может прийти человек,
обладающий достаточной способностью разбираться в философских вопросах.
И. Ньютон
Действительно, если вы потеряли в лесу родных или знакомых, рекомендуется кричать «ау!». Правда, тут нет пустоты - акустические волны распространяются в воздухе. Но во Вселенной громадную роль играют волны, способные распространяться и в вакууме.
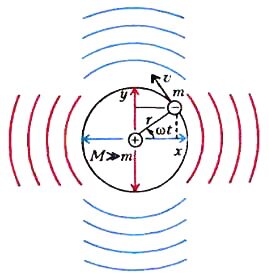
Представим себе два заряда противоположного знака - один тяжелый положительный, другой легкий отрицательный, вращающийся вокруг первого (рис.1). Кто подумал, что это атом водорода с протоном в центре, — не совсем прав, поскольку микромир нужно описывать при помощи квантовой механики, а мы собираемся остаться в рамках «обычной» физики. Просто имеем два заряда, и один из них вращается вокруг другого.
Ясно, что это вращение можно представить как два взаимно перпендикулярных колебания со сдвигом фаз на \(~\frac{\pi}{2}\):
(ибо, как хорошо известно, \(~\sin \omega t = \cos \left(\omega t - \frac{\pi}{2} \right)\)). Тут мы еще раз вспомнили , что даже равномерное движение по окружности есть ускоренное движение, да не одно, а два. Можно сказать также, что мы имеем два диполя (с переменным расстоянием между зарядами).
Но, как учат в школе (и правильно делают), каждый колеблющийся заряд излучает, причем мощность этого излучения пропорциональна четвертой степени частоты. В результате осциллятор - в нашем случае это диполь - каждую секунду должен терять свою энергию W так, что
Выразим энергию диполя через расстояние между зарядами r и величину заряда q. Сила их кулоновского взаимодействия (притяжения) равна
следовательно, потенциальная энергия взаимодействия есть
Кинетическую энергию \(~W_k = \frac{m \upsilon^2}{2}\) (центральный заряд тяжел и «неподвижен») можно переписать с учетом того, что кулоновская сила обеспечивает центростремительное ускорение, равное
Тогда полная энергия системы, равная сумме потенциальной и кинетической энергий, будет
(отрицательный знак описывает тот факт, что движущийся заряд не может уйти «на бесконечность»).
Поработаем теперь над выражением (1), стараясь уравнять хотя бы размерности его обеих частей.
Прежде всего заметим, что изменение энергии в единицу времени пропорционально самой энергии в данный момент времени. Это довольно общее положение. Например, убыль атомов. некоего радиоактивного изотопа пропорциональна имеющемуся количеству атомов:
где τ — характерное время распада, откуда получается экспоненциальный закон
Или, увеличение числа микробов в питательном бульоне в единицу времени пропорционально их наличному количеству:
откуда опять-таки
Точно так же скорость роста денежного вклада в банке пропорциональна наличности в данный момент (если не учитывать «черных» вторников, сред,...).
Таким образом, выражение (1) можно уже несколько конкретизировать:
В результате слева имеем размерность 1/с, справа 1/с4. Далее, поскольку речь идет об электромагнитном излучении, совершенно естественно вспомнить о скорости света в вакууме c, которая имеет размерность м/с и содержит в знаменателе так нужную нам секунду в первой степени:
Но что это - теперь справа в знаменателе стоит лишний м3. А у нас как раз есть характерный размер r! Запишем:
Наконец, с размерностями все в порядке, но это все еще не равенство: мы не знаем, какой безразмерный множитель может появиться в правой части. Ну и Бог с ним - мы и так знаем достаточно много. Например, можно оценить характерное время τ, за которое энергия осциллятора заметно изменится (например, в два раза):
Если говорить об излучении атома в оптическом диапазоне, можно взять ω ~ 1016 с-1, r ~ 10-10 м = 1 А. Тогда
С точки зрения «доквантовой» механики, за это характерное время все электроны должны были бы упасть на ядра своих атомов и Вселенная прекратила бы свое существование, по крайней мере в комфортном для нас виде. Этот Конец Света предотвратила квантовая механика: она позволила электронам вращаться на некоторых избранных (квантованных) уровнях достаточно долго. Но наша оценка не бесполезна: она оказалась оценкой характерного времени перехода между этими разрешенными уровнями.
Однако перейдем теперь к излучению другого рода - гравитационному. Вселенной управляет всемирное тяготение. И даже если муха в соседнем доме перелетит с одной стены на другую, это в принципе изменит распределение гравитационного поля во всей Вселенной, в том числе и у вашего рабочего стола. И это изменение передается при помощи гравитационных волн, которые распространяются со скоростью с, как и электромагнитные волны в вакууме. Только, в отличие от последних, от гравитационных волн нельзя экранироваться — они проникают всюду, но именно потому их и нелегко зарегистрировать. А было бы так заманчиво следить за перемещением любого интересующего нас тела!
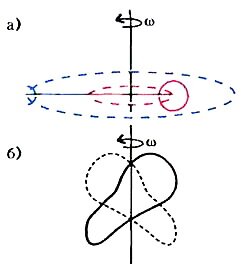
Конечно, полет мухи мало что изменит во Вселенной. Другое дело — движения небесных тел. Основными источниками гравитационных волн являются быстро вращающиеся пульсары, входящие в двойные звездные системы (рис. 2,а); ими могут быть также неосесимметричные волчки (рис. 2,б). Иными словами, для излучения гравитационных волн важна определенная асимметрия систем; их излучение является не дипольным, а квадрупольным. (Те, кто бывал на дискотеках, понимают, что «квадро» означает «четыре».)
Попробуем описать это излучение. Если гравитирующий волчок можно охарактеризовать массой m, характерным размером r и скоростью вращения ω, то легко понять, что его вращательная энергия \(~W \sim m r^2 \omega^2\). Оказывается, скорость убыли этой энергии тоже пропорциональна ω4, так что, аналогично выражению (2), можно записать
Однако сюда должны войти величины, характерные именно для гравитации — конечно же, постоянная всемирного тяготения G, имеющая размерность Н·м2/кг2 , и скорость распространения c с размерностью м/с:
Но теперь справа имеем размерность 1/(с·м2·кг), а нужна 1/с. Ясно, что правую часть надо умножить на mr2 — и все будет в порядке:
По этому выражению можно найти и характерное время τ замедления вращения звездной системы, излучающей гравитационные волны. Но это предоставим жителям ее планет... если кому-то нравится жить в поле двойной звезды.