Kvant. Энергия молекулы

Стасенко А.Л. Кладовые энергии молекулы //Квант. — 1995. — № 5. — С. 36-38.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Да неужто у молекулы, такой маленькой, могут быть еще и кладовые? ! А вот есть же. Они даже специальное название имеют: внутренние степени свободы. Но прежде всего напомним, что такое степень свободы.

Рис. 1

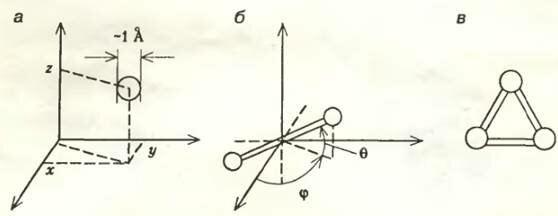
Положение в пространстве маленького тела, например атома (или материальной точки как математического предела маленького шарика), можно задать при помощи трех чисел x, y и z (рис.1, а). Этот атом можно переместить вдоль любой из трех осей независимо от двух других. Физики говорят, что у такого тела три степени свободы (i = 3). В комнатных условиях физическим образом такого шарика может служить атом благородного газа (гелия, неона, аргона, криптона, ксенона, радона).

Соединив две материальные точки жестким невесомым стержнем, получим нечто вроде гантельки (рис. 1, б). Для полного описания ее положения в пространстве нужны уже не только три числа x, y и z (которые теперь будут характеризовать положение центра масс гантельки), но еще и два угла φ и θ (в географии они называются долготой и широтой). Итак, как говорят герои «Приключений Буратино», три плюс два — сколько? — правильно, — пять степеней свободы (i = 5). А можно сказать и так: поскольку шариков два, то, будь они независимы друг от друга, для описания их положения в трехмерном пространстве потребовалось бы 3 x 2 = 6 чисел, но у них есть одна жесткая связь, так что в этом случае i = 3 x 2 — 1 = 5. Похоже, мы готовы нащупать некую общую формулу: i = 3 x N — S, где N — число материальных точек, S — число связей между ними.

Сделаем еще шаг — пусть есть три атома: N = 3, и они соединены тремя жесткими связями: S = 3 (рис. 1, в). Тогда получим i = 3 x 3 — 3 = 6. Действительно, в таком случае для описания положения этого треугольника в трехмерном пространстве нужен еще один угол — например, угол поворота плоскости треугольника относительно линии, соединяющей какую-нибудь пару атомов. Похоже, наша формула верна.

Рис. 2

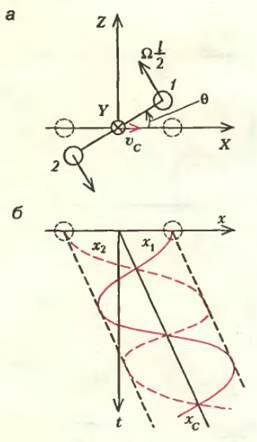
Теперь попробуем описать движение этих простых жестких молекул. Рассмотрим, например, гантельку, центр масс которой С движется вдоль оси X со скоростью υ_C, а сама гантелька длиной l вращается в плоскости XZ с постоянной угловой скоростью Ω (рис. 2, а). Угол θ при этом пропорционален времени: θ = Ωt (в начальный момент времени θ = 0 — гантелька расположена вдоль оси X). Тогда для обоих атомов имеем

\(~\begin{matrix} x_{1,2} = \upsilon_c t \pm \frac l2 \cos \Omega t \\ y_{1,2} = 0 \\ z_{1,2} = \pm \frac l2 \sin \Omega t\end{matrix}\) .

На рисунке 2, б показано изменение со временем только координат х обоих атомов и центра масс гантельки. Понятно, что в точках пересечения всех трех кривых гантелька расположена вдоль оси Z.

Рис. 3

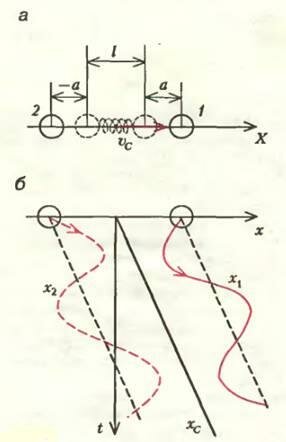
А почему гантельки обязательно жесткие? Представим себе, что два шарика (атома) массой m соединены пружинкой жесткостью К и могут скользить вдоль невесомого жесткого стержня (рис.З.а). В положении равновесия расстояние между ними l. Растянем пружинку так, чтобы каждый шарик отклонился от своего положения равновесия на величину ±а, и отпустим. Пусть при этом центр масс гантельки движется со скоростью υ_C вдоль оси X, а вращения нет. Тогда положение обоих шариков на оси X можно описать выражением

\(~x_{1,2} = \upsilon_c t \pm \left(\frac l2 + a \right) \cos \omega t\) ,

где \(~\omega = \sqrt{\frac{m}{2K}}\) — частота колебаний, и представить графически на рисунке 3,б. (А теперь вообразите, что есть еще и вращение, и попробуйте сами нарисовать суммарное движение шариков.)

В комнатных условиях молекулы основных компонентов воздуха — азота N₂ и кислорода О₂ — похожи на жесткие гантельки. Но с нагреванием газа в каждой молекуле возникают колебания атомов относительно центра масс. Говорят, что возбуждаются колебательные степени свободы. При дальнейшем увеличении температуры эти колебания могут стать столь интенсивными, что молекула развалится на атомы — произойдет ее диссоциация. Каждый образовавшийся атом-шарик (материальная точка) вновь будет иметь три степени свободы (но надо помнить, что атомов стало вдвое больше).

И еще надо помнить, что атом никакая не точка: это — многоэтажный дом, заселенный электронами, живущими в правовом обществе по законам квантовой механики. Эти электроны при столкновениях атомов могут забрасываться на верхние этажи (возбуждаются электронные степени свободы) или сбрасываться вниз, что сопровождается электромагнитным излучением. В очень важном частном случае — когда у атомов есть так называемый метастабильный уровень, на котором электроны могут «подождать» и «пожить» дольше, чем на обычном уровне, — можно создать... лазер. В лазере все электроны, как по команде, прыгают вниз, излучая мощную электромагнитную волну.

Это напоминает веселую задачу «Геофизическое «оружие» из «Физического фейерверка» (М.: Мир, 1979, с.163): «Китайская Народная Республика, возможно, обладает новым устрашающим видом оружия — геофизическим. Некоторые специалисты считают, что если все население Китая ... одновременно спрыгнет с двухметровых платформ, то в земле начнет распространяться ударная волна. Прыгая снова всякий раз, как эта волна будет проходить через Китай (каждые 53—54 мин), китайцы могут усилить ее до такой степени, что она может разрушить отдельные районы Соединенных Штатов, особенно в Калифорнии, нередко и сейчас страдающие от землетрясений».

Но что это мы все об электронах? Вернемся к молекулам, как было обещано в заглавии статьи. Пусть молекула из N атомов с S связями обладает числом степеней свободы i. Сюда входят три поступательные (или трансляционные) степени свободы i_t = 3, две или три вращательные и др. Какая нужна энергия, чтобы нагреть газ до температуры Т? Вспомним, что температура связана со средней энергией (приходящейся на одну молекулу) только поступательных степеней свободы молекулы:

\(~E_{cp} = \frac{kT}{2} + \frac{kT}{2} + \frac{kT}{2} = \frac 32 kT = \frac{i_t}{2} kT\) ,

где k — постоянная Больцмана. В этой записи учтен так называемый принцип равнораспределения энергии по степеням свободы: на каждую поступательную степень свободы при термодинамическом равновесии приходится в среднем энергия \(~\frac{kT}{2}\). Этот принцип иногда называют теоремой, иногда законом, иногда постулатом о равнораспределении энергии по степеням свободы. Важно не название. Важно другое — что он распространяется не только на поступательные, но и на любые степени свободы молекулы. Это означает, что для нагревания до температуры Т газа, молекулы которого обладают при этой температуре i степенями свободы, нужно каждую из них «накормить» энергией \(~\frac{kT}{2}\). Так что в результате потребуется в среднем, в расчете на одну молекулу, энергия

\(~E_i = \frac{1}{2} ikT\) ,

в расчете на один моль, содержащий число молекул, равное постоянной Авогадро N_A, -

\(~E_N = E_i N_A = \frac{1}{2} ikN_AT = \frac{1}{2} iRT\) ,

где R — универсальная газовая постоянная, в расчете на один килограмм —

\(~E = \frac{E_N}{M} = \frac{1}{2} i \frac RM T\) ,

где М — молярная масса. Напомним, что множитель при Т называется среднемолекулярной, молярной или удельной теплоемкостью соответственно.

Вернемся к колебательному движению молекул. Сколько степеней свободы соответствуют колебаниям вдоль одной линии? Оказывается, две: нужно знать не только положение относительно равновесия, но и скорость. С точки зрения энергии: одинаковый вклад (\(~\frac{kT}{2}\)) дает как средняя кинетическая энергия атомов, так и средняя потенциальная энергия их взаимодействия. Таким образом, если для жесткой гантельки i = 5, то в случае замены жесткого стерженька одномерной пружинкой i = 7.

А почему, — спросит вдумчивый читатель, — для описания, например, вращательного движения вокруг одной оси достаточно одной степени свободы? Ведь можно было бы потребовать задать и угол, и угловую скорость?!

Рис. 4

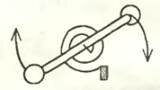
Да, так оно и было бы, если бы мы на ось жесткой вращающейся молекулы-гантельки надели спиральную пружинку (рис.4). Тогда при ее закручивании на некоторый угол появилась бы, помимо кинетической энергии шариков гантельки, еще и потенциальная энергия закрученной пружинки. Так что для достижения термодинамического равновесия пришлось бы «отвесить» не только \(~\frac{kT}{2}\) на среднюю кинетическую энергию молекулы, но и еще \(~\frac{kT}{2}\) на среднюю потенциальную энергию. А пока этой спиральной пружинки нет, одна вращательная степень свободы удовлетворяется одним \(~\frac{kT}{2}\).

Кстати, стрелки многих измерительных приборов как раз и похожи на то, что показано на рисунке 4. Они могут вращаться вокруг оси, а к положению равновесия их возвращает пружинка. Чем легче стрелка, тем чувствительнее прибор, что есть хорошо. Но если массу стрелки сделать близкой к массе молекул окружающей среды, то под действием ударов этих молекул прибор перестанет «работать»: стрелка будет участвовать в хаотическом тепловом движении. Это и будет тепловой предел измерений.

Строго говоря, любой предмет — стол, паровоз — находится в состоянии хаотического движения, точнее, центр масс этого предмета мечется во все стороны, согласно закону равнораспределения.

Среднеквадратичная поступательная скорость υ этого движения найдется из уравнения

\(~\frac{m \upsilon^2}{2} = \frac 32 kT\) ,

но так как масса тела велика, то скорость этого хаотического метания очень мала (оцените сами). Поэтому паровозы и не сходят с рельсов из-за теплового движения, а столы стоят на месте почти неподвижно.

Но мы не напрасно сказали выше слова «молекулы которого обладают при данной температуре i степенями свободы». Они подчеркивают, что при рассматриваемой температуре могут быть «включены» не все степени свободы молекулы. Так, при низких температурах молекулы летают как точки-шарики: их средняя энергия равна \(~\frac 32 kT\), «включены» только 3 трансляционные степени свободы, а остальные i — 3 степени свободы — кладовые, закрытые для насыщения их энергией. Молекулы при этом не только не колеблются, но и не вращаются, даже если они похожи на гантельки.

Рис. 5

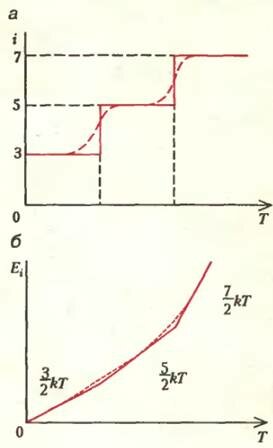
Это — чисто квантово-механический эффект (о чем приятно вспомнить на страницах «Кванта»). Оказывается, даже вращательная энергия квантуется: она не может быть меньше некоторой порции. Поэтому, если температура низка, эта минимальная порция еще не обеспечена, и вращения нет. Например, для молекулярного водорода Н₂ вращение включается при Т ~ 100 К, при Т ~ 1000 К включаются колебания и т.д., так что температурные зависимости числа степеней свободы и энергии имеют вид ломаных (рис.5). Конечно, в реальности эти изломы сглажены за счет разброса, или распределения, молекул по скоростям — см. штриховые линии на рисунке.

Но нужны ли нам все эти степени свободы молекул? Очень даже нужны — и не только из любви к свободе. Ведь мы нагреваем газ и наполняем кладовые энергии молекул теплотой не бесцельно: мы собираемся потом получить от газа работу (в паровой машине, двигателе внутреннего сгорания) или импульс (когда выбрасываем газ из сопла ракеты). И вот тут-то есть надежда, что газ вернет нам в виде желанного полезного эффекта тем больше «проглоченной» тепловой энергии, чем больше степеней свободы у его молекул. Увы, только надежда. Оказывается, в процессе расширения, т.е. совершения работы, начинает сказываться тот факт, что для достижения термодинамически равновесного состояния при изменяющейся со временем температуре T(t) для разных степеней свободы нужно неодинаковое число столкновений молекул друг с другом (а иначе — не сталкиваясь — как они узнают, что существуют другие молекулы и что температура газа-хаоса изменяется?). Больше всего столкновений требуется для колебательных степеней свободы. Поэтому газ может так быстро проскочить, например, сопло ракеты, охлаждаясь при этом и ускоряясь (мы и стремимся его разогнать как можно быстрее), что не все внутренние степени свободы успеют отдать свою энергию. В результате ускоренный газ, выброшенный в космос, будет холодным с точки зрения поступательных степеней свободы, но горячим с точки зрения внутренних степеней: из-за сильного разрежения молекулы почти перестанут сталкиваться, а их атомы будут яростно колебаться, храня память о высокой температуре где-то внутри двигателя. Возникает многотемпературная термодинамически неравновесная среда, в которой

T_колеб ≠ T_вращ ≠ T.

Это одна из интереснейших и важнейших задач физической газодинамики, которую можно изучить, например, на факультете аэромеханики и летательной техники Московского физико-технического института. Чего вам и желаем.