Kvant. Колебания и равновесие

Городецкий Е.Е. Гармонические колебания и равновесие //Квант. — 1987. — № 9. — С. 42-44.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Что мы изучаем, рассматривая колебания грузика, подвешенного на нитке или на пружинке? Два конкретных движения или нечто большее?

Оказывается, за «элементарными» движениями грузика стоит огромный, поистине неисчерпаемый мир колебаний. В природе колеблется все. Колеблются электроны внутри атома, атомы внутри молекулы, молекулы внутри кристалла. Колеблются дома, мосты и любые другие механические конструкции. Колеблется количество щук и карасей в водоемах, волков и зайцев в лесах. И так можно было бы продолжать до бесконечности.

Каждое колебание характеризуется своей частотой ω (или периодом \(~T = \frac{2\pi}{\omega}\)), и частота эта является важнейшей характеристикой любой колеблющейся системы. Так, например, частоты колебаний атомов в кристаллах определяют физические свойства кристаллов: их теплоемкость, теплопроводность, электрическое сопротивление и т. д. Частоты колебаний механических конструкций связаны с их прочностью и устойчивостью по отношению ко всякого рода механическим воздействиям. Некоторые электрические системы (генераторы, антенны и т. п.), в сущности, специально создаются для того, чтобы получить колебания определенных, нужных нам частот. Понятно поэтому, как важно уметь находить частоты колебаний, возникающих в различных системах. Но прежде чем рассказать, как это делается, обсудим, почему вообще колебания так распространены в природе.

Мы привыкли к тому, что мир вокруг нас довольно устойчив. Дома и мосты не разрушаются, корабли не переворачиваются, волки и зайцы устойчиво сосуществуют друг с другом. Кажется вполне очевидным, что тело, лежащее на дне ямы, самопроизвольно никогда не «выползет» из нее, в то время как лежащее на вершине горки тело вполне может взять да и скатиться вниз. Так вот, в определенном смысле и дом, и мост, и корабль на воде чрезвычайно похожи на лежащее на две ямы тело. Похожи тем, что все они находятся в положении устойчивого равновесия.

Оказывается, устойчивость равновесия и колебания тесно связаны друг с другом. Всякий раз когда в физике заходит речь о поведении или свойствах системы вблизи ее положения, равновесия, возникает задача о колебаниях, или, как ее часто называют, задача об осцилляторе. К осциллятору сводится большое число проблем современной физической науки.

Устойчивое равновесие характеризуется тем, что потенциальная энергия системы в этом положении минимальна. Именно благодаря этому и возникают колебания. Действительно, отклонив систему из положения равновесия, мы тем самым увеличили ее потенциальную энергию. В системе при этом возникают силы, стремящиеся вернуть ее обратно (уменьшить потенциальную энергию). Если предоставить такую систему самой себе, то она начнет «разгоняться», «скатываясь» к своему положению равновесия (как шарик в ямке). Избыточная потенциальная энергия переходит в энергию, связанную с движением, то есть в кинетическую. При прохождении положения равновесия «скорость» системы максимальна (вся потенциальная энергия перешла в кинетическую), и система проскакивает это положение. В дальнейшем «скорость» начинает уменьшаться, кинетическая энергия вновь переходит в потенциальную и т. д. Возникают колебания.

Мы не случайно слова «разгоняться» и «скорость» поставили в кавычки. Дело в том, что величина \(~\upsilon = \frac{\Delta x}{\Delta t}\) (Δx — «смещение» тела из положения равновесия), которая играет роль скорости, иногда совпадает с настоящей скоростью, а иногда нет (чуть ниже мы поясним это на примерах). Но независимо от этого кинетическая энергия всегда пропорциональна квадрату этой величины, т. е.

\(~W_k \sim \left( \frac{\Delta x}{\Delta t} \right)^2\) .

Так как для движущегося тела \(~W_k = \frac{m \upsilon^2}{2}\), то и в более общем случае кинетическую энергию принято записывать в виде

\(~W_k = \frac{m}{2} \left( \frac{\Delta x}{\Delta t} \right)^2\) .

Величина m здесь часто совпадает с массой, но в принципе может и отличаться от нее.

Потенциальная энергия произвольной системы вблизи положения устойчивого равновесия может быть записана в виде

\(~W_p = \frac{k}{2} (\Delta x)^2\) .

Множитель \(~\frac{1}{2}\) здесь введен просто для удобства (для симметрии с выражением \(~W_k = \frac{m \upsilon^2}{2}\)), коэффициент k в каждом конкретном случае свой, а величина Δx, как уже говорилось,— малое «смещение» тела из положения равновесия.

При описании любого физического явления энергия играет, пожалуй, самую фундаментальную роль. Хотя бы потому, что закон ее сохранения сильно ограничивает возможные типы движения. Чрезвычайно важна она и в нашем случае. Сделаем некоторое общее утверждение:

Если полная энергия системы, равная сумме потенциальной и кинетической энергий, в произвольный момент времени записывается в виде

\(~W = \frac{k (\Delta x)^2}{2} + \frac{m}{2} \left( \frac{\Delta x}{\Delta t} \right)^2\) .

то это означает, во-первых, что система колеблется и, во-вторых, что квадрат частоты колебаний равен отношению коэффициентов, определяющих потенциальную и кинетическую энергии, т. е. \(~\omega^2 = \frac{k}{m}\).

Вот мы и сформулировали основное правило нахождения частот колебаний. Проиллюстрируем сказанное на примерах.

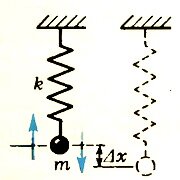
Пример первый (совсем простой) — тело на пружинке.

Роль потенциальной энергии в этом случае играет энергия упругой деформации (k — жесткость пружины). Из общего утверждения получаем

\(~\begin{matrix} W = \frac{k}{2} (\Delta x)^2 + \frac{m}{2} \left( \frac{\Delta x}{\Delta t} \right)^2 \\ \omega^2 = \frac{k}{m} \\ T = 2 \pi \sqrt{\frac{m}{k}} \end{matrix}\) .

Аналогично находятся частоты любых упругих колебаний: молекул в кристалле, Останкинской телебашни или моста через залив в Сан-Франциско и т. п.

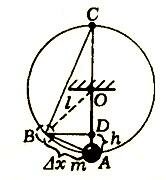
Пример второй (чуть сложнее) — математический маятник.

При записи потенциальной энергии материальной точки в поле тяготения надо учесть, что в выражении \(~W_p = mgh\) величина \(~h = \frac{(\Delta x)^2}{2l}\) (это следует из подобия треугольников ABD и ABC). Тогда из общего утверждения следует:

\(~\begin{matrix} W = \frac{mg}{2l} (\Delta x)^2 + \frac{m}{2} \left( \frac{\Delta x}{\Delta t} \right)^2 \\ \omega^2 = \frac{g}{l} \\ T = 2 \pi \sqrt{\frac{l}{g}} \end{matrix}\) .

Аналогично находятся частоты колебаний шарика в ямке, корабля на воде и т. д.

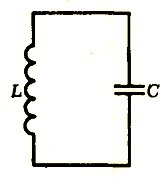
Пример третий (электрический) — колебательный контур.

В равновесии ни заряда на конденсаторе (С), ни тока через катушку (L) нет. При отклонении от равновесия на конденсаторе появляется заряд ΔQ, а через катушку течет ток \(~I = \frac{\Delta Q}{\Delta t}\). Роль потенциальной энергии играет энергия заряженного конденсатора\[~W_p = \frac{(\Delta Q)^2}{2C}\] (ведь именно она связана с взаимным расположением зарядов). Роль кинетической энергии берет на себя энергия, запасенная в катушке\[~W_k = \frac{LI^2}{2} = \frac{L}{2} \left(\frac{\Delta Q}{\Delta t} \right)^2\] (она связана с током, т. е. с движением зарядов; \(~I = \frac{\Delta Q}{\Delta t}\) играет роль скорости). Итак,

\(~\begin{matrix} W = \frac{1}{2C} (\Delta Q)^2 + \frac{L}{2} \left( \frac{\Delta Q}{\Delta t} \right)^2 \\ \omega^2 = \frac{1}{LC} \\ T = 2 \pi \sqrt{LC} \end{matrix}\) .

Определение частот колебаний по виду энергии оказывается удобным и в любом другом случае.

В заключение хочется сказать, что колебания не есть один из типов движения в ряду многих других, а представляют собой фундаментальное явление, элемент того таинственного «алфавита», с помощью которого природа создает все, что нас окружает.