SA. Напряженность поля
Электрическое поле
Рассмотренный ранее закон Кулона устанавливает количественные и качественные особенности взаимодействия точечных электрических зарядов в вакууме. Однако этот закон не дает ответа на весьма важный вопрос о механизме взаимодействия зарядов, т.е. посредством чего передается действие одного заряда на другой. Поиск ответа на этот вопрос привел английского физика М. Фарадея к гипотезе о существовании электрического поля, справедливость которой была полностью подтверждена последующими исследованиями. Согласно идее Фарадея электрические заряды не действуют друг на друга непосредственно. Каждый из них создает в окружающем пространстве электрическое поле. Поле одного заряда действует на другой заряд, и наоборот.
Все сказанное позволяет дать следующее определение:
- электрическое поле – это особый вид материи, посредством которого осуществляется взаимодействие электрических зарядов.
Свойства электрического поля
- Электрическое поле материально, т.е. существует независимо от наших знаний о нем.
- Порождается электрическим зарядом: вокруг любого заряженного тела существует электрическое поле.
- Поле, созданное неподвижными электрическими зарядами, называется электростатическим.
- Электрическое поле может быть создано и переменным магнитным полем. Такое электрическое поле называется вихревым.
- Обнаружить электрическое поле можно по действию его на электрические заряды с некоторой силой.
- Электрическое поле распространяется в пространстве с конечной скоростью, равной скорости света в вакууме.
- Таким образом, если один из взаимодействующих зарядов переместить в другую точку пространства, то второй заряд почувствует изменение положения первого заряда не мгновенно, а спустя некоторый промежуток времени \(~\Delta t = \dfrac{l}{c}\), где с — скорость света в вакууме, l — расстояние между зарядами.
Напряженность электрического поля
Недостаточно утверждать, что электрическое поле существует. Надо ввести количественную характеристику поля. После этого электрические поля можно будет сравнивать друг с другом и продолжать изучать их свойства. Электрическое поле обнаруживается по силам, действующим на электрический заряд. Можно утверждать, что мы знаем о поле все, что нужно, если будем знать силу, действующую на любой заряд в любой точке поля. Поэтому надо ввести такую характеристику поля, знание которой позволит определить эту силу.
Для изучения электрического поля будем использовать пробный заряд.
- Под пробным зарядом будем понимать положительный точечный заряд, не изменяющий изучаемое электрическое поле.
Пусть электрическое поле создается точечным зарядом q0. Если в это поле внести пробный заряд q1, то на него будет действовать сила \(~\vec F\).
- Обратите внимание, что в данной теме мы используем два заряда: источник электрического поля q0 и пробный заряд q1. Электрическое поле действует только на пробный заряд q1 и не может действовать на свой источник, т.е. на заряд q0.
Согласно закону Кулона эта сила пропорциональна заряду q1:
Поэтому отношение силы, действующей на помещаемый в данную точку поля заряд q1, к этому заряду в любой точке поля:
не зависит от помещенного заряда q1 и может рассматриваться как характеристика поля. Эту силовую характеристику поля называют напряженностью электрического поля.
Подобно силе, напряженность поля – векторная величина, ее обозначают буквой \(~\vec E\) .
- Напряженность поля равна отношению силы, с которой поле действует на точечный заряд, к этому заряду:
- Сила, действующая на заряд q со стороны электрического поля, равна\[~\vec F = q \cdot \vec E\] .
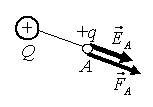
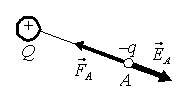
Если в точке А заряд q > 0, то векторы \(~\vec E_A\) и \(~\vec F_A\) направлены в одну и ту же сторону; при q < 0 эти векторы направлены в противоположные стороны.
- От знака заряда q, на который действует поле, не зависит направление вектора \(~\vec E_A\), а зависит направление силы \(~\vec F_A\) (рис. 1, а, б).
- В СИ напряженность выражается в ньютонах на кулон (Н/Кл).
Значение напряженности электрического поля, созданного:
-
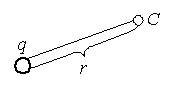
точечным зарядом q, на расстоянии r от заряда в точке C (рис. 2) равно
-
\(~E = k \cdot \dfrac{|q|}{r^2}\) .
-
-
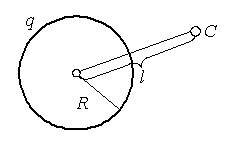
сферой радиуса R с зарядом q, на расстоянии l от центра сферы в точке C (рис. 3), равно
-
\(~E = k \cdot \dfrac{|q|}{l^2}\) , если l ≥ R; -
\(~E = 0\) , если l < R.
-
-
заряженной бесконечной пластиной с поверхностной плотностью заряда σ, равно
-
\(~E = \dfrac{|\sigma|}{2 \varepsilon_0}\) , - где \(~\sigma = \dfrac{q}{S}\) , q – заряд плоскости, S – площадь плоскости.
-
Принцип суперпозиции полей
А чему будет равна напряженность в некоторой точке электрического поля, созданного несколькими зарядами q1, q2, q3, …?
Поместим в данную точку пробный заряд q. Пусть F1 — это сила, с которой заряд q1 действует на заряд q; F2 — это сила, с которой заряд q2 действует на заряд q и т.д. Из динамики вы знаете, что если на тело действует несколько сил, то результирующая сила равна геометрической сумме сил, т.е.
Разделим левую и правую часть уравнения на q :
Если учтем, что \(\dfrac{ \vec F}{q} = \vec E\), мы получим, так называемый, принцип суперпозиции полей
- напряженность электрического поля, созданного несколькими зарядами q1, q2, q3, …, в некоторой точке пространства равна векторной сумме напряженностей \(\vec E_1 , \, \vec E_2 , \, \vec E_3\), … полей, создаваемых каждым из этих зарядов:
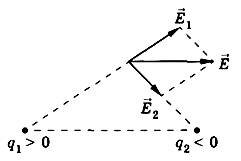
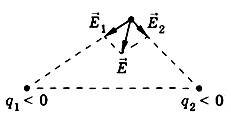
Благодаря принципу суперпозиции для нахождения напряженности поля системы точечных зарядов в любой точке достаточно знать выражение для напряженности поля точечного заряда. На рисунке 4, а, б показано, как геометрически определяется напряженность \(~\vec E\) поля, созданного двумя зарядами.
- Для определения напряженности поля, создаваемого заряженным телом конечных размеров (не точечных зарядов), нужно поступать следующим образом. Мысленно разделить тело на маленькие элементы, каждый из которых можно считать точечным. Определить заряды всех этих элементов и найти напряженности полей, созданных всеми ими в заданной точке. После этого сложить геометрически напряженности от всех элементов тела и найти результирующую напряженность поля. Для тел сложной формы это трудная, но в принципе разрешимая задача. Для ее решения нужно знать, как заряд распределен на теле.
Линии напряженности
Электрическое поле не действует на органы чувств. Его мы не видим. Тем не менее распределение поля в пространстве можно сделать видимым. Английский физик Майкл Фарадей в 1845 году предложил изображать электрическое поле с помощью силовых линий и получал своеобразные карты, или диаграммы поля.
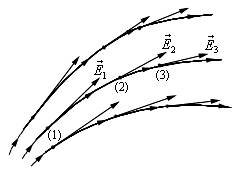
- Силовая линия (или линия напряженности) — это воображаемая направленная линия в пространстве, касательная к которой в каждой точке совпадают с направлением вектора напряженности в этой точке (рис. 5).
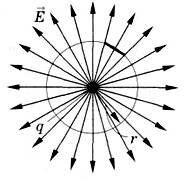
По картине силовых линий можно судить не только о направлении вектора , но и о его значении. Действительно, для точечных зарядов напряженность поля увеличивается по мере приближения к заряду, а силовые линии при этом сгущаются (рис. 6). Где силовые линии гуще там напряженность больше и наоборот.
- Число силовых линий, приходящихся на поверхность единичной площади, расположенную нормально к силовым линиям, пропорционально модулю напряженности.
Картины силовых линий
Построить точную картину силовых линий заряженного тела – сложная задача. Нужно сначала вычислить напряженность поля Е(х, у, z) как функцию координат. Но этого еще мало. Остается непростая задача проведения непрерывных линий так, чтобы в каждой точке линии касательная к ней совпадала с направлением напряженности \(~\vec E\) . Такую задачу проще всего поручить компьютеру, работающему по специальной программе.
Впрочем, строить точную картину распределения силовых линий не всегда необходимо. Иногда достаточно рисовать приближенные картины, не забывая что:
- силовые линии — это незамкнутые линии: они начинаются на поверхности положительно заряженных тел (или в бесконечности) и оканчиваются на поверхности отрицательно заряженных тел (или в бесконечности);
- силовые линии не пересекаются, так как в каждой точке поля вектор напряженности имеет лишь одно направление;
- между зарядами силовые линии нигде не прерываются.
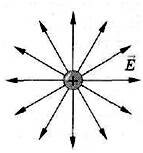
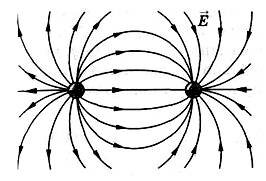
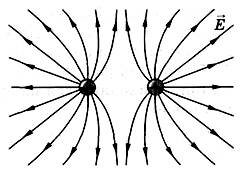
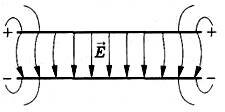
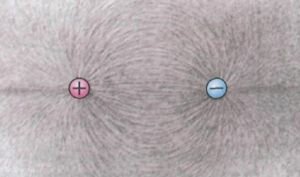
На рисунках 7–10 изображены картины силовых линий: положительно заряженного шарика (рис. 7); двух разноименно заряженных шариков (рис. 8); двух одноименно заряженных шариков (рис. 9); двух пластин, заряды которых равны по модулю и противоположны по знаку (рис. 10).
На рисунке 10 видно, что в пространстве между пластинами вдали от краев пластин силовые линии параллельны: электрическое поле здесь одинаково во всех точках.
- Электрическое поле, напряженность которого одинакова во всех точках пространства, называется однородным.
Не следует думать, что линии напряженности – это существующие в действительности образования вроде растянутых упругих нитей или шнуров, как предполагал сам Фарадей. Линии напряженности лишь помогают представить распределение поля в пространстве и не более реальны, чем меридианы и параллели на земном шаре.
Однако силовые линии можно сделать «видимыми». Для этого нужно металлические тела (электроды) соединить с полюсами электростатической машины и погрузить в вязкий диэлектрик (например, в касторовое или вазелиновое масло). В эту жидкость надо насыпать и хорошо перемешать продолговатые частицы изолятора (например, вискозы, асбеста, манной крупы, семян или мелко настриженный волос). При заряжении электродов в жидкости создается достаточно сильное электрическое поле. Под влиянием электрического поля частицы диэлектрика поляризуются: на их концах появляются заряды противоположного знака. Частицы поворачиваются во внешнем поле вдоль линий напряженности, и заряды на их концах взаимодействуют друг с другом. Разно именные заряды притягиваются, а одноименные отталкиваются. В результате частицы диэлектрика вы страиваются вдоль силовых линий (рис. 11).
Литература
- Жилко, В. В. Физика: учеб. пособие для 11-го кл. общеобразоват. учреждений с рус. яз. обучения с 12-летним сроком обучения (базовый и повышенный уровни) /В. В. Жилко, Л. Г. Маркович. — 2-е изд., исправленное. — Минск: Нар. асвета, 2008. — С. 75, 80-85.
- Мякишев Г.Я. Физика: Электродинамика. 10-11 кл.: учеб. для углубленного изучения физики / Г.Я. Мякишев, А.З. Синяков, Б.А. Слободсков. – М.: Дрофа, 2005. – 476 с.