КС. Равноускоренное движение

Равноускоренное движение

Мгновенная скорость характеризует неравномерное движение в данный момент времени или в данной точке траектории.

При прямолинейном движении ускорение направлено:

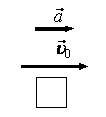
• в сторону движения (скорости), если скорость тела увеличивается (рис. 1 а);
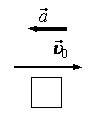
• в противоположную сторону движения (скорости), если скорость тела уменьшается (рис. 1 б).

И наоборот:

• если направления ускорения и движения (скорости) совпадают, то скорость тела увеличивается (см. рис. 1 а);
• если ускорение направлено в противоположную сторону движения (скорости), то скорость тела уменьшается (см. рис. 1 б).

• 

  а
• 

  б

Рис. 1 \(~\vec a = \frac{\vec \upsilon - \vec \upsilon_0}{t} ; a_x = \frac{\upsilon_x - \upsilon_{0x}}{t}\) ,

где \(~\vec a\) – вектор ускорения (м/с²); а_x – проекция ускорения на ось 0Х (м/с²); \(~\vec \upsilon_0\) – вектор начальной скорости (скорость тела в начальный момент времени) (м/с); \(~\vec \upsilon\) – вектор конечной скорости (скорость тела через некоторый промежуток времени) (м/с); υ_x, υ_0x – проекции этих скоростей на ось 0Х (м/с); t – время, в течении которого изменяется скорость (с).

Скрытые данные:

• Тело начало двигаться (трогается с места) – υ₀ = 0 м/с.
• Тело остановилось – υ = 0 м/с.
• Скорость тела уменьшается – ускорение направлено против движения.

Во всех задачах этой темы считаем движение тел прямолинейным. Ось 0Х будем направлять вдоль движения (начальной скорости). В этом случае к скрытым данным добавляем:

• если скорость тела увеличивается, то а_x > 0;
• если скорость тела уменьшается, то а_x < 0.

\(~t = \frac{\upsilon_x - \upsilon_{0x}}{a_x}\) ,

где t – время, в течении которого изменяется скорость (с); а_x – проекция ускорения на ось 0Х (м/с²); υ_0x – проекция начальной скорости на ось 0Х (м/с); υ_x – проекция конечной скорости на ось 0Х (м/с).

\(~\upsilon_x = \upsilon_{0x} + a_x \cdot t\) ,

где υ_x – проекция конечной скорости на ось 0Х (м/с); υ_0x – проекция начальной скорости на ось 0Х (м/с); а_x – проекция ускорения на ось 0Х (м/с²); t – время, в течении которого изменяется скорость (с).

\(~\Delta r_x = \upsilon_{0x} \cdot t + \frac{a_x \cdot t^2}{2}\) ,

где Δr_x – проекция перемещения на ось 0Х (м); υ_0x – проекция начальной скорости на ось 0Х (м/с); t – время, в течении которого совершается перемещение (с); a_x – проекция ускорения на ось 0Х (м/с²).

\(~\Delta r_x = \frac{\upsilon^2_x - \upsilon^2_{0x}}{2 a_x}\) ,

где Δr_x – проекция перемещения на ось 0Х (м); υ_x – проекция конечной скорости на ось 0Х (м/с); υ_0x – проекция начальной скорости на ось 0Х (м/с); a_x – проекция ускорения на ось 0Х (м/с²).

\(~\Delta r_x = \upsilon_x \cdot t - \frac{a_x \cdot t^2}{2}\) ,

где Δr_x – проекция перемещения на ось 0Х (м); υ_x – проекция конечной скорости на ось 0Х (м/с); t – время, в течении которого совершается перемещение (с); a_x – проекция ускорения на ось 0Х (м/с²).

\(~\Delta r_x = \frac{\upsilon_x + \upsilon_{0x}}{2} \cdot t\) ,

где Δr_x – проекция перемещения на ось 0Х (м); υ_x – проекция конечной скорости на ось 0Х (м/с); υ_0x – проекция начальной скорости на ось 0Х (м/с); t – время, в течении которого совершается перемещение (с).

Уравнения движения

В уравнениях (1)-(5) используются пять величин: проекции перемещения Δr_x, проекции начальной скорости υ_0x, проекции конечной скорости υ_x, проекции ускорения a_x и времени t (таблица).

№	Формула	Используемые величины	Отсутствующие величины
1	\(~\Delta r_x = \upsilon_{0x} \cdot t + \frac{a_x \cdot t^2}{2}\)	Δrx, υ0x, ax и t	υx
2	\(~\Delta r_x = \upsilon_x \cdot t - \frac{a_x \cdot t^2}{2}\)	Δrx, υx, ax и t	υ0x
3	\(~\Delta r_x = \frac{\upsilon^2_x - \upsilon^2_{0x}}{2 a_x}\)	Δrx, υ0x, υx и ax	t
4	\(~\Delta r_x = \frac{\upsilon_x + \upsilon_{0x}}{2} \cdot t\)	Δrx, υ0x, υx и t	ax
5	\(~\upsilon_x = \upsilon_{0x} + a_x \cdot t\)	υ0x, υx, ax и t	Δrx

По этим величинам можно определить, какой формулой лучше всего пользоваться. Например, если требуется найти перемещение Δr_x, а известны υ_x, υ_0x и a_x, то можно воспользоваться формулой (3), т.к. отсутствует время t.

К используемым относятся величины, которые заданы по условию, и величины, которые нужно найти.

Виды прямолинейного движения относительно оси:

• вдоль оси, если проекция скорости υ_0x > 0;
• начинает движение вдоль оси, если υ_0x = 0, а a_x > 0;
• против оси, если проекция скорости υ_0x < 0;
• начинает движение против оси, если υ_0x = 0, а a_x < 0;
• покоится, если υ_0x = 0 и a_x = 0;
• равномерное, если υ_0x ≠ 0, а a = 0;
• равноускоренное с увеличением скорости, если знаки проекций на данную ось скорости и ускорения совпадают или υ_0x = 0, а a_x ≠ 0;
• равноускоренное с уменьшением скорости (равнозамедленное), если знаки проекций на данную ось скорости и ускорения не совпадают.
• Если движение равноускоренное с уменьшением скорости, то через некоторый промежуток времени проекция скорости тела станет равной нулю (тело остановилось), а затем тело станет двигаться в противоположную сторону.

Условие встречи двух тел:

х₁(t_встр) = х₂(t_встр); y₁(t_встр) = y₂(t_встр) …