Слободянюк А.И. Физика 10/12.13
§12. Постоянное магнитное поле
12.13 Применение теоремы о циркуляции к расчету магнитного поля.
12.13.1 Поле цилиндрического проводника с током.
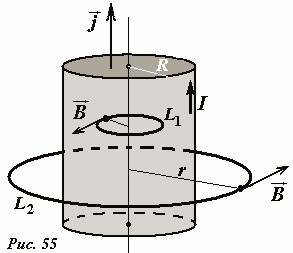
Постоянный электрический ток силой I протекает по длинному цилиндрическому проводнику радиуса R (Рис. 55). Найдем распределение индукции магнитного в пространстве, как внутри цилиндра, так и вне его. Будем считать, что ток равномерно распределен по поперечному сечению цилиндра, то есть плотность тока является постоянной и равной
Это предположение выглядит логичным, однако не обоснованным, на самом деле, расчет распределения плотности тока является отдельной сложной задачей.
Можно повторить все рассуждения и экспериментальные обоснования, которые привели нас к выводу о том, что силовые линии магнитного поля прямого тока являются концентрическими окружностями. В данном случае симметрия задачи также осевая, поэтому и здесь силовые линии – окружности с центрами на оси цилиндра. Для расчета величины магнитной индукции, конечно, допустимо использовать закон Био-Саварра-Лапласа и принцип суперпозиции. Но зачем идти таким длинным путем, если есть возможность воспользоваться теоремой о циркуляции вектора магнитной индукции. Сначала в качестве контура L1 выберем окружность радиуса r, совпадающую с одной из силовых линий, которая расположена внутри цилиндра. На этой окружности вектор индукции направлен по касательной к контуру (это же силовая линия) и постоянен по модулю, поэтому циркуляция вектора индукции равна произведению ее модуля на длину окружности \(~\Gamma_B = B \cdot 2 \pi r\) . Сила тока, пересекающего контур, равна произведению плотности тока на площадь круга, ограниченного рассматриваемым контуром \(~I_1 = j \cdot \pi r^2 = I \frac{r^2}{R^2}\) . По известной теореме, циркуляция вектора магнитной индукции равна электрическому току, пресекающему контур, умноженному на магнитную постоянную, поэтому справедливо равенство
из которого находим значение индукции поля
которая возрастает пропорционально расстоянию до оси цилиндра.
Если вычислить циркуляцию для кругового контура L2, радиус r которого превышает радиус цилиндра, то она, по-прежнему, будет равна \(~\Gamma_B = B \cdot 2 \pi r\) , но сила тока, пересекающего контур, будет равна I (весь ток пересекает контур), поэтому теорема о циркуляции для этого контура будет иметь вид
из которой следует, что магнитное поле в рассматриваемом случае совпадает с полем прямого тока, индукция которого равна
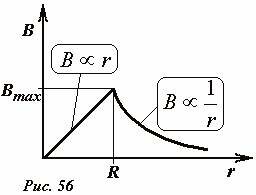
и убывает обратно пропорционально расстоянию до оси цилиндра. На поверхности цилиндра (при r = R) формулы (2) и (3) приводят к одному и тому же результату, здесь индукция поля максимальна \(~B_{max} = \frac{\mu_0 I}{2 \pi R}\) .
Важно отметить, что распределение магнитного поля вне цилиндра не зависит от распределения плотности тока внутри цилиндра, если это распределение сохраняет осевую симметрию. Поэтому если поле создается электрическими токами, протекающими по тонким проводам, то нас не интересует распределение плотности тока в поперечном сечении.
График зависимости индукции поля от расстояния до оси цилиндра приведен на рис. 56.
12.13.2 Поле пластины с током.
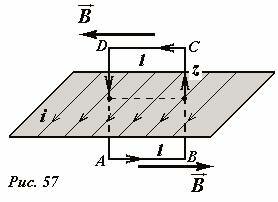
Электрический ток равномерно протекает по очень большой пластине (то есть будем считать ее бесконечной), линейная плотность тока равна i (Рис.57). Найдем индукцию магнитного поля, Создаваемого таким распределением токов.
В том случае, когда электрический ток протекает по тонкой пластине, можно пренебречь толщиной пластины, или распределением плотности тока по глубине, то распределение токов на поверхности удобно характеризовать линейной плотностью – отношением силы тока, пересекающего малый отрезок, перпендикулярный направлению тока, к длине этого отрезка
Линейную плотность тока можно считать вектором, указывающим направление движения зарядов.
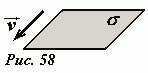
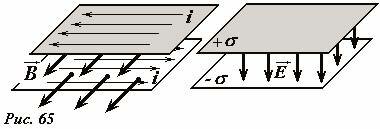
Линейная плотность тока является некоторым аналогом поверхностной плотности заряда – когда можно пренебречь толщиной слоя, в котором находятся заряды, можно считать, что все заряды находятся на поверхности, и описывать их распределение поверхностной плотностью σ. Кстати, равномерное распределение поверхностных токов можно получить, если равномерно заряженную пластину (с постоянной плотностью заряда σ) двигать с постоянной скоростью \(~\vec \upsilon\) , направленной вдоль плоскости пластины (Рис. 58). В этом случае линейная плотность электрического тока равна \(~\vec i = \sigma \vec \upsilon\) (докажите это самостоятельно).
Вернемся к расчету магнитного поля. Прежде всего, нам необходимо попытаться определить направление вектора индукции этого поля. Используя симметрию задачи можно утверждать, что вектор индукции может зависеть только от расстояния до плоскости (если сместится на некоторое расстояние вдоль плоскости, то распределение токов не изменится, почему должно изменится создаваемое им поле?). Поле под плоскостью совпадет с полем над плоскостью при его повороте на 180° (при таком повороте распределение токов на плоскости не изменяется).
Далее – вектор индукции такого поля не может иметь составляющей, перпендикулярной пластине, иначе не будет выполняться теорема о магнитном потоке.
Наконец, прямой электрический ток, создает магнитное поле, вектор индукции которого перпендикулярен направления тока – откуда в данной задаче взяться составляющей вектора индукции, параллельной току?
Таким образом, мы приходим к выводу, что вектор индукции изучаемого поля и его силовые линии направлены параллельно пластине и перпендикулярно направлению тока (Рис. 57).
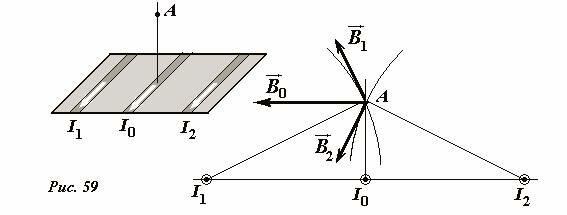
К этому же выводу можно прийти на основании принципа суперпозиции. Для этого следует разбить плоскость на ряд очень тонких полосок, параллельных направлению тока, которые можно рассматривать как линейные токи (Рис. 59).
Затем следует просуммировать [1] векторы индукции полей, создаваемых каждой полоской. Понятно, что на бесконечной плоскости каждой полоске I1 (за исключением I0, той, которая находится непосредственно под точкой наблюдения A) найдется симметричная ей I2. Сумма векторов индукции полей, создаваемых симметричными полосками, направлена параллельно плоскости и перпендикулярно току (так же как и вектор индукции центральной полоски I0). Следовательно, и сумма векторов индукции полей, создаваемых всеми полосками направлена также.
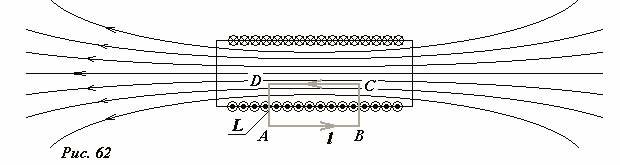
Все эти рассуждения нам необходимы, чтобы выбрать контур для подсчета циркуляции в виде прямоугольника ABCD (Рис. 57), симметричного относительно пластины, плоскость которого перпендикулярна пластине и направлению тока, а две его стороны параллельны пластине (длины этих сторон обозначим l). На сторонах BC и DA вектор индукции перпендикулярен им (поэтому здесь \(~\vec B \cdot \Delta \vec l = 0\)), а на сторонах параллельных плоскости вектор индукции постоянен и направлен вдоль контура (поэтому на каждой из этих сторон \(~\sum_k \vec B_k \cdot \Delta \vec l_k = Bl\)). Таким образом, циркуляция вектора индукции по данному контуру равна \(~\Gamma_B = 2 Bl\) . Используя теорему о циркуляции, запишем уравнение
(где \(I = il\) - сила тока, пересекающего контур) из которого определим индукцию поля
Во-первых, полученный результат говорит, что магнитное поле является однородным - его индукция постоянна (заранее мы не могли утверждать, что она не зависит от расстояния до пластины). Во-вторых, полученная формула удивительно похожа на формулу для напряженности поля равномерно заряженной пластины (если правильно поменять магнитную и электрическую постоянные); правда, вектор напряженности перпендикулярен пластине, а вектор индукции параллелен ей.
12.13.3 Поле соленоида.
Соленоидом называется цилиндрическая катушка с проволочной обмоткой, по которой можно пропускать электрический ток (Рис. 60). Такой прибор широко используется в различных приборах для создания магнитного поля и других целей.
Сейчас наша задача – рассчитать характеристики магнитного поля, создаваемого электрическим током, протекающим по обмотке. Будем считать, что все параметры катушки (соленоида) нам известны. Для этого, прежде всего, необходимо качественно обсудить структуру магнитного поля. Первое, самое очевидное, источник обладает осевой симметрией, поэтому создаваемое им поле также должно быть осесимметричным, поэтому достаточно рассмотреть структуру поля (например, его силовые линии).
Далее воспользуемся способом рассуждений Майкла Фарадея, который с каждым электрическим зарядом связывал определенное число силовых линий электрического поля исходящих из заряда (своеобразная трактовка теоремы Гаусса), а с каждым элементом тока определенное число замкнутых силовых линий магнитного поля (теорема о циркуляции индукции магнитного поля).
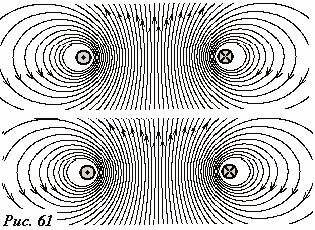
Соленоид является совокупностью параллельных практически плоских круговых витков, поле которого мы изучали. Посмотрим еще раз на силовые линии поля одного витка (На Рис. 61 показаны поля двух витков – каждое из которых часть рисунка 33). Силовые линии должны охватить проводник с током, поэтому они сгущаются внутри витка, а снаружи удаляются от него. Если сблизить два витка, то силовые линии начнут охватывать оба проводника (токи в них текут в одном направлении), что приведет к еще большему сгущению внутри витков и удалению от них снаружи. Добавление числа витков будет усиливать этот эффект. Поэтому следует ожидать, что для длинного соленоида с большим числом витков, силовые линии внутри соленоида будут почти прямыми линиями с небольшими искривлениями при приближении к границам катушки (Рис. 62), а снаружи от него будут замыкаться где-то очень далеко от катушки.
Проведем еще одну цепочку рассуждений, приводящих к такому же выводу о структуре магнитного поля соленоида.
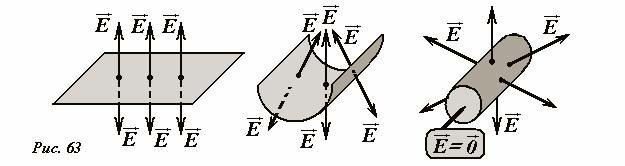
Сначала рассмотрим электрическое поле равномерно заряженной плоскости, которое является однородным с каждой стороны от плоскости и зеркально симметричным. А затем мысленно свернем часть плоскости в цилиндрическую трубку (Рис. 63). Внутри векторы напряженности окажутся направленными противоположно друг другу, поэтому скомпенсируют друг друга – поле внутри равномерно заряженного цилиндра отсутствует, а снаружи будет радиальным (Рис. 63).
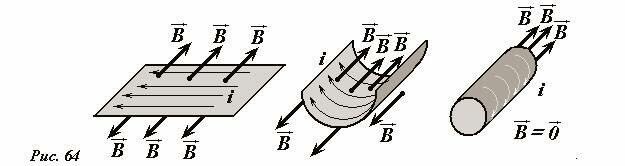
Теперь «сделаем» соленоид из участка плоскости, по которой равномерно протекает электрический ток. В этом случае силовые линии внутри цилиндра сгущаются, а снаружи имеют возможность «разбежаться» (Рис. 64).
Интересная конструкция получится, если расположить параллельно две плоских пластины, по которым токи текут в противоположных направлениях. В этом случае магнитное поле будет создаваться только между пластинами, так как снаружи поля пластин направлены противоположно и компенсируют друг друга. Не напоминает ли эта система плоский конденсатор? Похожая ситуация и в случае соленоида – снаружи вблизи соленоида магнитное поле отсутствует.
Задание для самостоятельной работы.
- «Сверните» мысленно из части плоскости, по которой течет постоянный электрический ток, цилиндр так, чтобы ток тек вдоль цилиндра (параллельно его оси). Установите структуру магнитного поля, создаваемого этим током.
После того, как структура поля установлена, расчет величины индукции поля является «примитивной задачкой». Выберем контур (см. Рис. 62) для применения теоремы о циркуляции в виде прямоугольника ABCD, стороны которого AB и CD параллельны оси катушки. Подсчет циркуляции вектора индукции магнитного поля (то есть суммы \(~\Gamma_B = \sum_i \vec B_i \cdot \Delta \vec l_i\)) в рассматриваемом случае прост: на стороне AB магнитное поле отсутствует; на сторонах BC и DA вектор индукции перпендикулярен контуру (поэтому соответствующие слагаемые также равны нулю); на стороне CD вектор индукции постоянен и параллелен этой стороне, поэтому здесь \(~\sum_i \vec B_i \cdot \Delta \vec l_i = Bl\) (l - длина этой стороны контура). Таким образом, уравнение теоремы о циркуляции в данном случае имеет вид
где N - число витков обмотки, которые попали внутрь выбранного контура. Из этого уравнения находим индукцию магнитного поля внутри соленоида
где \(~n = \frac{N}{l}\) - число витков обмотки на единицу длины соленоида, эта величина также называется плотностью намотки.
Из окончательной формулы (2) следует, что поле внутри длинного соленоида является однородным. При приближении к торцам соленоида начинают сказываться, так называемые, краевые эффекты: во-первых, поле перестает быть однородным, появляются радиальные составляющие вектора индукции (силовые линии изгибаются), во-вторых, величина индукции поля уменьшается.
Задание для самостоятельной работы.
Покажите, в точке находящейся в центре торца соленоида, индукция поля уменьшается в два раза по сравнению с индукцией поля в точках далеких от торцов. (Подсказка: мысленно присоедините к рассматриваемому торцу еще один такой же соленоид).
Примечания
- ↑ Еще раз обратим внимание – здесь суммирование проводится по источникам, а точка наблюдения фиксирована.
Смотреть HD
видео онлайн
бесплатно 2022 года