Kvant. Еще раз о м. силе
Ромишевский Е. Еще раз о магнитной силе //Квант. — 2000. — № 3. — С. 38-39.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
В статье «Эта загадочная магнитная сила» говорилось о свойствах электромагнитной силы Лоренца. Здесь же мы обсудим, как взаимодействуют между собой ее электрическая и магнитная составляющие и какова природа магнитной силы Ампера, действующей на проводник с током в магнитном поле.
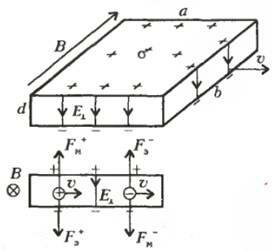
Рассмотрим сначала взаимодействие магнитной и электрической сил на примере поступательного движения проводящего бруска в однородном магнитном поле (рис.1). Пусть магнитное поле \(~\vec B\) направлено перпендикулярно вектору постоянной скорости \(~\vec \upsilon\) и плоской грани ad прямоугольного бруска со сторонами а, b, d. Будем считать, что брусок имеет форму «плоского конденсатора»: сторона d много меньше сторон а и b.
Как известно, в узлах жесткой кристаллической решетки металла расположены положительные ионы, а свободные электроны равномерно распределены по его объему. При движении бруска в магнитном поле на положительные заряды бруска е+ и отрицательные заряды е- действуют магнитные силы, равные по величине \(~F_m = e \upsilon B\) и направленные в противоположные стороны. Под действием магнитной силы свободные электроны смещаются вниз и создают на верхней и нижней поверхностях бруска избыточные заряды с поверхностными плотностями σ+ и σ-. Это приводит к тому, что внутри бруска, как в плоском конденсаторе, возникает однородное электрическое кулоновское поле \(~\vec E_{\perp}\) , вызывающее электрическую силу, которая компенсирует действие магнитной силы в объеме бруска. Магнитная сила как бы вызывает электрическую силу, чтобы себя уравновесить:
В результате такой «плоский конденсатор» оказывается заряженным до разности потенциалов
В целом брусок остается электрически нейтральным, электрические заряды возникают только на поверхностях бруска и в равных количествах (σ+ = σ-).
При равномерном движении бруска в однородном магнитном поле полная сила, действующая на брусок, естественно, равна нулю. Однако при ускорении бруска, т.е. при увеличении скорости \(~\vec \upsilon\), или при вхождении в область увеличивающегося магнитного поля \(~\vec B\) брусок будет испытывать со стороны магнитного поля силу торможения. При этом будут, соответственно, увеличиваться и напряженность электрического поля \(~\vec E_{\perp}\), и поверхностные плотности зарядов σ+ и σ- .
Заметим, что равномерно движущийся в магнитном поле проводящий брусок представляет собой прообраз главного элемента самых мощных и самых распространенных источников электрической энергии, электродвижущая сила ε которых определяется именно магнитной силой\[~\varepsilon = \upsilon B d\].
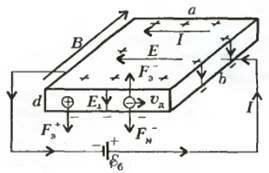
Пусть теперь наш металлический брусок abd неподвижен и имеет омическое сопротивление R. Подключим к его граням bd (рис.2) батарею с электродвижущей силой εb так, чтобы обеспечить в бруске постоянный по любому сечению bd электрический ток \(~I = \frac{\varepsilon_b}{R}\) . Поскольку разность потенциалов между сечениями bd равна εb, в объеме бруска установится однородное электрическое поле \(~\vec E\), параллельное сторонам а. Под влиянием этого поля свободные электроны металла будут дрейфовать вправо со средней скоростью υd, создавая электрический ток
где n - плотность свободных электронов, е - их заряд, а S = bd - площадь сечения. Нужно отметить, что направление движения электронов со скоростью ад противоположно направлению электрического поля \(~\vec E\) и направлению электрического тока I. Положительно заряженные ионы, образующие жесткую кристаллическую решетку, естественно, при этом покоятся.
Если внешнее магнитное поле отсутствует, то единственным магнитным полем будет собственное магнитное поле \(~\vec B_c\), возникающее при движении свободных электронов, которым мы можем пренебречь. Теперь включим внешнее магнитное поле \(~\vec B\), точно такое же, как и в предыдущем случае. Под действием возникшей магнитной силы, равной \(~F_m = e \upsilon_d B\), движущиеся со скоростью υd электроны будут отклоняться вниз и создавать избыток отрицательных зарядов на нижней поверхности бруска и положительных на его верхней поверхности. Так будет продолжаться до тех пор, пока не возникнет поперечное электрическое поле \(~\vec E_{\perp}\), направленное вниз и компенсирующее действие магнитной силы, - точно так же, как это было в случае равномерного движения бруска в однородном магнитном поле. Принципиальное отличие заключается в том, что при наличии электрического тока в движении участвуют только свободные электроны. В стационарном состоянии, которое достигается очень быстро после включения внешнего магнитного поля, электроны в среднем снова движутся горизонтально вдоль сторон а, а внутри металлического бруска появляется поперечное электрическое поле \(~E_{\perp} = \frac{\sigma}{\varepsilon_0}\), наблюдаемое в системе отсчета, связанной с кристаллической решеткой металла. Это поле своим действием уравновешивает магнитную силу, действующую на движущиеся электроны, и создает электрическую силу \(~\vec F_e\) , направленную вниз и действующую на неподвижные положительные ионы (на кристаллическую решетку металла).
Вот таким образом магнитная сила, действующая на электроны, передается сплошному металлическому бруску. Величину этой воспринимаемой бруском силы можно записать так:
- на один положительный ион действует сила, равная
-
\(~F_{\perp} = e E_{\perp} = e \upsilon_d B\) ,
- на все же ионы бруска, а их N = nabd, где n - число ионов в единице объема (равное плотности свободных электронов), будет действовать сила, равная
-
\(~F_N = e \upsilon_d B \cdot nabd = ne \upsilon_d bd \cdot B \cdot a = IBa\) ,
Как и следовало ожидать, эта сила в точности равна сумме всех сил Лоренца, действующих со стороны магнитного поля на движущиеся электроны. Силу, действующую на проводник длиной а, по которому течет ток I и который помещен в однородное магнитное поле \(~\vec B\), называют силой Ампера. А физическое явление возникновения разности потенциалов между поверхностями проводника (нашего бруска), когда по нему течет электрический ток и проводник находится в магнитном поле, называется эффектом Холла. Эту разность потенциалов
можно измерить непосредственно с помощью вольтметра. Заметим, что эффект Холла был открыт в 1879 году, за много лет до открытия электрона Томсоном (1897 г.).