А. Математический маятник
Математический маятник. Период колебаний математического маятника
Математическим маятником называют материальную точку, подвешенную на невесомой и нерастяжимой нити, прикрепленной к подвесу и находящейся в поле силы тяжести (или иной силы).
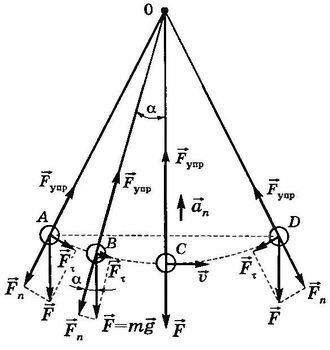
Исследуем колебания математического маятника в инерциальной системе отсчета, относительно которой точка его подвеса находится в покое или движется равномерно прямолинейно. Силой сопротивления воздуха будем пренебрегать (идеальный математический маятник). Первоначально маятник покоится в положении равновесия С. При этом действующие на него сила тяжести \(\vec F\) и сила упругости \(\vec F_{ynp}\) нити взаимно компенсируются.
Выведем маятник из положения равновесия (отклонив его, например, в положение А) и отпустим без начальной скорости (рис. 13.11). В этом случае силы \(\vec F\) и \(\vec F_{ynp}\) не уравновешивают друг друга. Тангенциальная составляющая силы тяжести \(\vec F_\tau\), действуя на маятник, сообщает ему тангенциальное ускорение \(\vec a_\tau\) (составляющая полного ускорения, направленная вдоль касательной к траектории движения математического маятника), и маятник начинает двигаться к положению равновесия с возрастающей по модулю скоростью. Тангенциальная составляющая силы тяжести \(\vec F_\tau\) является, таким образом, возвращающей силой. Нормальная составляющая \(\vec F_n\) силы тяжести направлена вдоль нити против силы упругости \(\vec F_{ynp}\). Равнодействующая сил \(\vec F_n\) и \(\vec F_{ynp}\) сообщает маятнику нормальное ускорение \(~a_n\), которое изменяет при этом направление вектора скорости, и маятник движется по дуге ABCD.
Чем ближе подходит маятник к положению равновесия С, тем меньше становится значение тангенциальной составляющей \(~F_\tau = F \sin \alpha\). В положении равновесия она равна нулю, а скорость достигает максимального значения, и маятник движется по инерции дальше, поднимаясь по дуге вверх. При этом составляющая \(\vec F_\tau\) направлена против скорости. С увеличением угла отклонения а модуль силы \(\vec F_\tau\) увеличивается, а модуль скорости уменьшается, и в точке D скорость маятника становится равной нулю. Маятник на мгновение останавливается, а затем начинает двигаться в обратном направлении к положению равновесия. Вновь пройдя его по инерции, маятник, замедляя движение, дойдет до точки А (трение отсутствует), т.е. совершит полное колебание. После этого движение маятника будет повторяться в уже описанной последовательности.
Получим уравнение, описывающее свободные колебания математического маятника.
Пусть маятник в данный момент времени находится в точке В. Его смещение S от положения равновесия в этот момент равно длине дуги СВ (т.е. S = |СВ|). Обозначим длину нити подвеса l, а массу маятника — m.
Из рисунка 13.11 видно, что \(~F_\tau = F \sin \alpha\), где \(\alpha =\frac{S}{l}.\) При малых углах \(~(\alpha <10^\circ)\) отклонения маятника \(\sin \alpha \approx \alpha,\) поэтому
Знак минус в этой формуле ставят потому, что тангенциальная составляющая силы тяжести направлена к положению равновесия, а смещение отсчитывают от положения равновесия.
Согласно второму закону Ньютона \(m \vec a = m \vec g + F_{ynp}.\) Спроецируем векторные величины этого уравнения на направление касательной к траектории движения математического маятника
Из этих уравнений получим
\(a_\tau = -\frac{g}{l}S\) — динамическое уравнение движения математического маятника. Тангенциальное ускорение математического маятника пропорционально его смещению и направлено к положению равновесия. Это уравнение можно записать в виде\[a_\tau+\frac{g}{l}S = 0\]. Сравнивая его с уравнением гармонических колебаний \(~a_x + \omega^2x = 0\) (см. § 13.3), можно сделать вывод, что математический маятник совершает гармонические колебания. А так как рассмотренные колебания маятника происходили под действием только внутренних сил, то это были свободные колебания маятника. Следовательно, свободные колебания математического маятника при малых отклонениях являются гармоническими.
Обозначим \(\frac{g}{l} = \omega^2.\) Откуда \(\omega = \sqrt \frac{g}{l}\) — циклическая частота колебаний маятника.
Период колебаний маятника \(T = \frac{2 \pi}{\omega}.\) Следовательно,
Это выражение называют формулой Гюйгенса. Оно определяет период свободных колебаний математического маятника. Из формулы следует, что при малых углах отклонения от положения равновесия период колебаний математического маятника: 1) не зависит от его массы и амплитуды колебаний; 2) пропорционален корню квадратному из длины маятника и обратно пропорционален корню квадратному из ускорения свободного падения. Это согласуется с экспериментальными законами малых колебаний математического маятника, которые были открыты Г. Галилеем.
Подчеркнем, что эту формулу можно использовать для расчета периода при одновременном выполнении двух условий: 1) колебания маятника должны быть малыми; 2) точка подвеса маятника должна покоиться или двигаться равномерно прямолинейно относительно инерциальной системы отсчета, в которой он находится.
Если точка подвеса математического маятника движется с ускорением \(\vec a\) то при этом изменяется сила натяжения нити, что приводит к изменению и возвращающей силы, а следовательно, частоты и периода колебаний. Как показывают расчеты, период колебаний маятника в этом случае можно рассчитать по формуле
где \(~g'\) — "эффективное" ускорение маятника в неинерциальной системе отсчета. Оно равно геометрической сумме ускорения свободного падения \(\vec g\) и вектора, противоположного вектору \(\vec a\), т.е. его можно рассчитать по формуле
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — С. 374-376.