А. Ток в металлах
Электронная проводимость металлов
Электронная проводимость металлов была впервые экспериментально доказана немецким физиком Э.Рикке в 1901 г. Через три плотно прижатых друг к другу отполированных цилиндра — медный, алюминиевый и снова медный — длительное время (в течение года) пропускали электрический ток. Общий заряд, прошедший за это время, был равен 3.5·106 Кл. Поскольку массы атомов меди и алюминия существенно отличаются друг от друга, то массы цилиндров должны были бы заметно измениться, если бы носителями заряда были ионы. Результаты опытов показали, что масса каждого из цилиндров осталась неизменной. В соприкасающихся поверхностях были обнаружены лишь незначительные следы взаимного проникновения металлов, которые не превышали результатов обычной диффузии атомов в твердых телах. Следовательно, свободными носителями заряда в металлах являются не ионы, а такие частицы, которые одинаковы и в меди, и в алюминии. Такими частицами могли быть только электроны.
Прямое и убедительное доказательство справедливости этого предположения было получено в опытах, поставленных в 1913 г. Л. И. Мандельштамом и Н. Д. Папалекси и в 1916 г. Т. Стюартом и Р. Толменом.
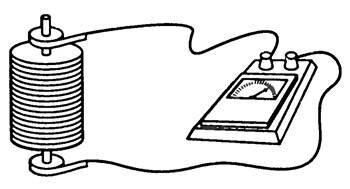
На катушку наматывают проволоку, концы которой припаивают к двум металлическим дискам, изолированным друг от друга (рис. 1). К концам дисков с помощью скользящих контактов присоединяют гальванометр.
Катушку приводят в быстрое вращение, а затем резко останавливают. После резкой остановки катушки свободные заряженные частицы будут некоторое время двигаться вдоль проводника по инерции, и, следовательно, в катушке возникнет электрический ток. Ток будет существовать короткое время, так как из-за сопротивления проводника заряженные частицы тормозятся и упорядоченное движение частиц прекращается.
Направление тока говорит о том, что он создается движением отрицательно заряженных частиц. Переносимый при этом заряд пропорционален отношению заряда частиц, создающих ток, к их массе, т.е. \(~\Delta q = \frac{q_0}{m}\). Поэтому, измеряя заряд, проходящий через гальванометр за все время существования тока в цепи, удалось определить отношение \(~\frac{q_0}{m}\). Оно оказалось равным 1,8·1011 Кл/кг. Эта величина совпадает с отношением заряда электрона к его массе, найденным ранее из других опытов.
Таким образом, электрический ток в металлах создается движением отрицательно заряженных частиц электронов. Согласно классической электронной теории проводимости металлов (П. Друде, 1900 г., Х.Лоренц, 1904 г.), металлический проводник можно рассматривать как физическую систему совокупности двух подсистем:
- свободных электронов с концентрацией ~ 1028 м-3 и
- положительно заряженных ионов, колеблющихся около положения равновесия.
Появление свободных электронов в кристалле можно объяснить следующим образом.
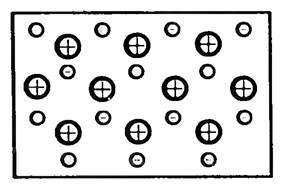
При объединении атомов в металлический кристалл слабее всего связанные с ядром атома внешние электроны отрываются от атомов (рис. 2). Поэтому в узлах кристаллической решетки металла располагаются положительные ионы, а в пространстве между ними движутся электроны, не связанные с ядрами своих атомов. Эти электроны называются свободными или электронами проводимости. Они совершают хаотическое движение, подобное движению молекул газа. Поэтому совокупность свободных электронов в металлах называют электронным газом.
Если к проводнику приложено внешнее электрическое поле, то на беспорядочное хаотическое движение свободных электронов накладывается направленное движение под действием сил электрического поля, что и порождает электрический ток. Скорость движения самих электронов в проводнике — несколько долей миллиметра в секунду, однако возникающее в проводнике электрическое поле распространяется по всей длине проводника со скоростью, близкой к скорости света в вакууме (3·108 м/с).
Так как электрический ток в металлах образуют свободные электроны, то проводимость металлических проводников называется электронной проводимостью.
Электроны под влиянием постоянной силы, действующей со стороны электрического поля, приобретают определенную скорость упорядоченного движения (ее называют дрейфовой). Эта скорость не увеличивается в дальнейшем со временем, так как при столкновении с ионами кристаллической решетки электроны передают кинетическую энергию, приобретенную в электрическом поле, кристаллической решетке. В первом приближении можно считать, что на длине свободного пробега λ (это расстояние, которое электрон проходит между двумя последовательными столкновениями с ионами) электрон движется с ускорением \(~a = \frac{eE}{m}\) и его дрейфовая скорость линейно возрастает со временем\[~\upsilon = at = \frac{eEt}{m}\]. В момент столкновения электрон передает кинетическую энергию кристаллической решетке. Потом он опять ускоряется, и процесс повторяется. В результате средняя скорость упорядоченного движения электронов пропорциональна напряженности электрического поля в проводнике \(~\mathcal h \upsilon \mathcal i \sim E\) и, следовательно, разности потенциалов на концах проводника, так как \(~E = \frac Ul\), где l — длина проводника.
Известно, что сила тока в проводнике пропорциональна скорости упорядоченного движения частиц\[~I = en \mathcal h \upsilon \mathcal i S\], а значит, согласно предыдущему, сила тока пропорциональна разности потенциалов на концах проводника: I ~ U. В этом состоит качественное объяснение закона Ома на основе классической электронной теории проводимости металлов.
Однако в рамках этой теории возникли трудности. Из теории следовало, что удельное сопротивление должно быть пропорционально корню квадратному из температуры (\(~\rho \sim \sqrt T\)), между тем, согласно опыту, ρ ~ Т. Кроме того, теплоемкость металлов, согласно этой теории, должна быть значительно больше теплоемкости одноатомных кристаллов. В действительности теплоемкость металлов мало отличается от теплоемкости неметаллических кристаллов. Эти трудности были преодолены только в квантовой теории.
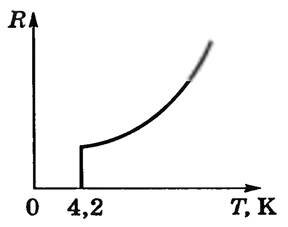
В 1911 г. голландский физик Г. Камерлинг-Оннес, изучая изменение электрического сопротивления ртути при низких температурах, обнаружил, что при температуре около 4 К (т.е. при -269 °С) удельное сопротивление скачком уменьшается (рис. 1) практически до нуля. Это явление обращения электрического сопротивления в нуль Г. Камерлинг-Оннес назвал сверхпроводимостью.
В дальнейшем было выяснено, что более 25 химических элементов — металлов при очень низких температурах становятся сверхпроводниками. У каждого из них своя критическая температура перехода в состояние с нулевым сопротивлением. Самое низкое значение ее у вольфрама — 0,012 К, самое высокое у ниобия — 9 К.
Сверхпроводимость наблюдается не только у чистых металлов, но и у многих химических соединений и сплавов. При этом сами элементы, входящие в состав сверхпроводящего соединения, могут и не являться сверхпроводниками. Например, NiBi, Au2Bi, PdTe, PtSb и другие.
Вещества в сверхпроводящем состоянии обладают необычными свойствами:
- электрический ток в сверхпроводнике может существовать длительное время без источника тока;
- внутри вещества в сверхпроводящем состоянии нельзя создать магнитное поле:
- магнитное поле разрушает состояние сверхпроводимости. Сверхпроводимость — явление, объясняемое с точки зрения квантовой теории. Достаточно сложное его описание выходит за рамки школьного курса физики.
Широкому применению сверхпроводимости до недавнего времени препятствовали трудности, связанные с необходимостью охлаждения до сверхнизких температур, для чего использовался жидкий гелий. Тем не менее, несмотря на сложность оборудования, дефицитность и дороговизну гелия, с 60-х годов XX века создаются сверхпроводящие магниты без тепловых потерь в их обмотках, что сделало практически возможным получение сильных магнитных полей в сравнительно больших объемах. Именно такие магниты требуются для создания установок управляемого термоядерного синтеза с магнитным удержанием плазмы, для мощных ускорителей заряженных частиц. Сверхпроводники используются в различных измерительных приборах, прежде всего в приборах для измерения очень слабых магнитных полей с высочайшей точностью.
В настоящее время в линиях электропередачи на преодоление сопротивления проводов уходит 10 - 15 % энергии. Сверхпроводящие линии или хотя бы вводы в крупные города принесут громадную экономию. Другая область применения сверхпроводимости — транспорт.
На основе сверхпроводящих пленок создан ряд быстродействующих логических и запоминающих элементов для счетно-решающих устройств. При космических исследованиях перспективно использование сверхпроводящих соленоидов для радиационной защиты космонавтов, стыковки кораблей, их торможения и ориентации, для плазменных ракетных двигателей.
В настоящее время созданы керамические материалы, обладающие сверхпроводимостью при более высокой температуре — свыше 100 К, то есть при температуре выше температуры кипения азота. Возможность охлаждать сверхпроводники жидким азотом, который имеет на порядок более высокую теплоту парообразования, существенно упрощает и удешевляет все криогенное оборудование, обещает огромный экономический эффект.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 279-282.