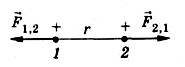Закон Кулона

Закон Кулона

В 1785 г. французский физик Шарль Кулон экспериментально установил основной закон электростатики – закон взаимодействия двух неподвижных точечных заряженных тел или частиц.

Закон взаимодействия неподвижных электрических зарядов – закон Кулона – основной (фундаментальный) физический закон и может быть установлен только опытным путем. Ни из каких других законов природы он не вытекает.

Если обозначить модули зарядов через |q₁| и |q₂|, то закон Кулона можно записать в следующей форме:

\(~F = k \cdot \dfrac{|q_1| \cdot |q_2|}{r^2}\) , (1)

где k – коэффициент пропорциональности, значение которого зависит от выбора единиц электрического заряда. В системе СИ \(~k = \dfrac{1}{4 \pi \cdot \varepsilon_0} = 9 \cdot 10^9\) Н·м²/Кл², где ε₀ – электрическая постоянная, равная 8,85·10^-12 Кл²/Н·м² .

Формулировка закона:

сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.

Эту силу называют кулоновской.

Закон Кулона в данной формулировке справедлив только для точечных заряженных тел, т.к. только для них понятие расстояния между зарядами имеет определенный смысл. Точечных заряженных тел в природе нет. Но если расстояние между телами во много раз больше их размеров, то ни форма, ни размеры заряженных тел существенно, как показывает опыт, не влияют на взаимодействие между ними. В этом случае тела можно рассматривать как точечные.

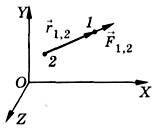
Легко обнаружить, что два заряженных шарика, подвешенные на нитях, либо притягиваются друг к другу, либо отталкиваются. Отсюда следует, что силы взаимодействия двух неподвижных точечных заряженных тел направлены вдоль прямой, соединяющей эти тела. Подобные силы называют центральными. Если через \(~\vec F_{1,2}\) обозначить силу действующую на первый заряд со стороны второго, а через \(~\vec F_{2,1}\) – силу, действующую на второй заряд со стороны первого (рис. 1), то, согласно третьему закону Ньютона, \(~\vec F_{1,2} = -\vec F_{2,1}\) . Обозначим через \(\vec r_{1,2}\) радиус-вектор, проведенный от второго заряда к первому (рис. 2), тогда

\(~\vec F_{1,2} = k \cdot \dfrac{q_1 \cdot q_2}{r^3_{1,2}} \cdot \vec r_{1,2}\) . (2)

• 

  Рис. 1
• 

  Рис. 2

Если знаки зарядов q₁ и q₂ одинаковы, то направление силы \(~\vec F_{1,2}\) совпадает с направлением вектора \(~\vec r_{1,2}\) ; в противном случае векторы \(~\vec F_{1,2}\) и \(~\vec r_{1,2}\) направлены в противоположные стороны.

Зная закон взаимодействия точечных заряженных тел, можно вычислить силу взаимодействия любых заряженных тел. Для этого тела нужно мысленно разбить на такие малые элементы, чтобы каждый из них можно было считать точечным. Складывая геометрически силы взаимодействия всех этих элементов друг с другом, можно вычислить результирующую силу взаимодействия.

Открытие закона Кулона – первый конкретный шаг в изучении свойств электрического заряда. Наличие электрического заряда у тел или элементарных частиц означает, что они взаимодействуют друг с другом по закону Кулона. Никаких отклонений от строгого выполнения закона Кулона в настоящее время не обнаружено.

Опыт Кулона

Необходимость проведения экспериментов Кулона была вызвана тем, что в середине XVIII в. накопилось много качественных данных об электрических явлениях. Возникла потребность дать им количественную интерпретацию. Поскольку силы электрического взаимодействия были относительно невелики, возникла серьезная проблема в создании метода, который позволил бы произвести замеры и получить необходимый количественный материал.

Французский инженер и ученый Ш. Кулон предложил метод измерения малых сил, который основывался на следующем экспериментальном факте, обнаруженном самим ученым: сила, возникающая при упругой деформации металлической проволоки, прямо пропорциональна углу закручивания, четвертой степени диаметра проволоки и обратно пропорциональна ее длине:

\(~F_{ynp} = k \cdot \dfrac{d^4}{l} \cdot \varphi\) ,

где d – диаметр, l – длина проволоки, φ – угол закручивания. В приведенном математическом выражении коэффициент пропорциональности k находился опытным путем и зависел от природы материала, из которого изготавливалась проволока.

Данная закономерность была использована в так называемых крутильных весах. Созданные весы позволили измерить ничтожно малые силы порядка 5·10^-8 Н.

• 

  а
• 

  б

Рис. 3

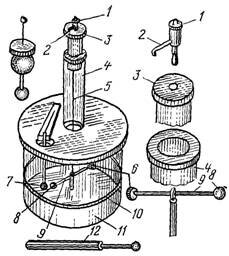
Крутильные весы (рис. 3, а) состояли из легкого стеклянного коромысла 9 длиной 10,83 см, подвешенного на серебряной проволоке 5 длиной около 75 см, диаметром 0,22 см. На одном конце коромысла располагался позолоченный бузиновый шарик 8, а на другом – противовес 6 – бумажный кружок, смоченный в скипидаре. Верхний конец проволоки прикреплялся к головке прибора 1. Здесь же имелся указатель 2, с помощью которого отсчитывался угол закручивания нити по круговой шкале 3. Шкала была проградуирована. Вся эта система размещалась в стеклянных цилиндрах 4 и 11. В верхней крышке нижнего цилиндра имелось отверстие, в которое вставлялась стеклянная палочка с шариком 7 на конце. В опытах применялись шарики с диаметрами в пределах 0,45 – 0,68 см.

Перед началом эксперимента указатель головки устанавливался на нулевой отметке. Затем шарик 7 заряжался от предварительно наэлектризованного шарика 12. При соприкосновении шарика 7 с подвижным шариком 8 происходило перераспределение заряда. Однако из-за того, что диаметры шариков были одинаковыми, одинаковыми были и заряды на шариках 7 и 8.

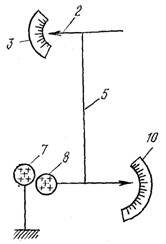
Вследствие электростатического отталкивания шариков (рис. 3, б) коромысло 9 поворачивалось на некоторый угол γ (по шкале 10). С помощью головки 1 это коромысло возвращалось в исходное положение. По шкале 3 указатель 2 позволял определять угол α закручивания нити. Общий угол закручивания нити φ = γ + α. Сила же взаимодействия шариков была пропорциональна φ, т. е. по углу закручивания можно судить о величине этой силы.

При неизменном расстоянии между шариками (оно фиксировалось по шкале 10 в градусной мере) исследовалась зависимость силы электрического взаимодействия точечных тел от величины заряда на них.

Для определения зависимости силы от заряда шариков Кулон нашел простой и остроумный способ изменения заряда одного из шариков. Для этого он соединял заряженный шарик (шарики 7 или 8) с таким же по размерам незаряженным (шарик 12 на изолирующей ручке). Заряд при этом распределялся поровну между шариками, что и уменьшало исследуемый заряд в 2, 4 и т. д. раз. Новое значение силы при новом значении заряда опять определялось экспериментально. При этом выяснилось, что сила прямо пропорциональна произведению зарядов шариков:

\(~F \sim q_1 \cdot q_2\) .

Зависимость силы электрического взаимодействия от расстояния была обнаружена следующим образом. После сообщения шарикам заряда (он был у них одинаковый) коромысло отклонялось на некоторый угол γ. Затем поворотом головки 1 уменьшался этот угол до γ₁. Общий угол закручивания φ₁ = α₁ + (γ - γ₁)(α₁ – угол поворота головки). При уменьшении углового расстояния шариков до γ₂ общий угол закручивания φ₂ = α₂ + (γ - γ₂) . Было замечено, что, если γ₁ = 2γ₂, ТО φ₂ = 4φ₁, т. е. при уменьшении расстояния в 2 раза сила взаимодействия возрастала в 4 раза. Во столько же раз увеличился момент силы, так как при деформации кручения момент силы прямо пропорционален углу закручивания, а значит, и сила (плечо силы оставалось неизменным). Отсюда вытекает вывод: сила взаимодействия двух заряженных шариков обратно пропорциональна квадрату расстояния между ними:

\(~F \sim \dfrac{1}{r^2}\) .

Литература

1. Мякишев Г.Я. Физика: Электродинамика. 10-11 кл.: учеб. для углубленного изучения физики / Г.Я. Мякишев, А.З. Синяков, Б.А. Слободсков. – М.: Дрофа, 2005. – 476 с.
2. Вольштейн С. Л. и др. Методы физической науки в школе: Пособие для учителя / С.Л. Вольштейн, С.В. Позойский, В.В. Усанов; Под ред. С.Л. Вольштейна. – Мн.: Нар. асвета, 1988. – 144 с.