КС. Закон сохранения энергии
Механическая работа. Мощность
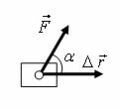
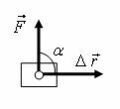
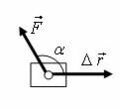
где А – работа (Дж); F – сила (Н); Δr – перемещение тела (м); α – угол между вектором силы и вектором перемещения (рис. 1).
- Данную формулу можно применять, если сила постоянна.
где Aтр – работа силы трения (Дж); Fтр – сила трения (Н); Δr – перемещение тела (м).
- Работа силы трения отрицательная, т.к. сила трения и относительное перемещение тела направлены в противоположные стороны.
где Р – мощность прибора (Вт); А – механическая работа, совершенная данным прибором (Дж); Δt – время, за которое совершена работа (с).
где η – коэффициент полезного действия (КПД) (%); Аp – полезная работа (Дж); Аz – затраченная работа (Дж).
- Полезная работа – это работа, которую совершает механизм над телом,
- затраченная работа – это работа двигателя или энергия (тепловая, электроэнергия и т.п.), которую механизм израсходует (получает).
Графический способ определения механической работы
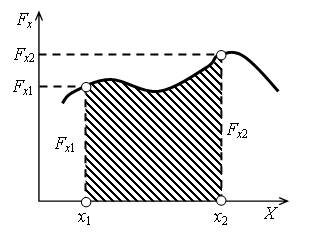
Пусть задан график зависимости проекции силы Fx от координаты х. Тогда работа при перемещении тела из точки с координатой x1 в точку с координатой x2 численно равна по величине площади фигуры, ограниченной графиком Fx(х), осью 0Х и перпендикулярами к x1 и x2 (рис. 2).
- При перемещении тела из точки с координатой x2 в точку с координатой x1 площадь фигуры и, следовательно, работу будем считать отрицательной.
- Если разные участки тела поднимают на разные высоты, то изменение потенциальной энергии можно рассчитать для центра тяжести тела.
- Центр тяжести стержня находится в середине стержня; прямоугольника – на пересечении диагоналей; шара, обруча – в центре сферы, окружности.
Механическая энергия
Кинетическая энергия тела
где Ek – кинетическая энергия тела (Дж); m – масса тела (кг); υ – скорость тела (м/с).
Теорема об изменении кинетической энергии
где A – механическая работа силы, действующей на тело (Дж); \(~\Delta E_k = \frac{m \cdot \upsilon^2}{2} - \frac{m \cdot \upsilon^2_0}{2}\) – изменение кинетической энергии тела (Дж); m – масса тела (кг); υ и υ0 – конечная и начальная скорости тела (м/с).
Потенциальная энергия взаимодействия тела и Земли
где Ep – потенциальная энергия тела (взаимодействия тела и Земли) (Дж); m – масса тела (кг); g – ускорение свободного падения, у поверхности Земли равна 9,8 м/с2 ≈ 10 м/с2; h – высота тела над нулевой высотой (м).
- За нулевую высоту (уровень), по умолчанию, принято считать поверхность земли.
где A – работа консервативных сил (силы тяжести) (Дж); ΔEp = mgh – mgh0 – изменение потенциальной энергии тела (взаимодействия тела и Земли) (Дж); m – масса тела (кг); g – ускорение свободного падения, у поверхности Земли равна 9,8 м/с2 ≈ 10 м/с2; h и h0 – конечная и начальная высоты тела над нулевой высотой (м).
- За нулевую высоту (уровень), по умолчанию, принято считать поверхность земли.
Потенциальная энергия деформированной пружины
где Ep – потенциальная энергия деформированной пружины (Дж); k – коэффициент жесткости пружины (Н/м); Δl = |l – l0| – абсолютное удлинение (удлинение) пружины (м); l и l0 – конечная и начальная длины пружины (м).
где A – работа консервативных сил (силы упругости) (Дж); \(~\Delta E_p = \frac{k \cdot \Delta l^2}{2} - \frac{k \cdot \Delta l^2_0}{2}\) – изменение потенциальной энергии пружины (Дж); k – коэффициент жесткости пружины (Н/м); Δl и Δl0 – конечное и начальное абсолютные удлинения (конечное и начальное удлинения) пружины (м).
- По умолчанию считаем, что пружина вначале не деформирована, т.е. Δl0 = 0.
Закон сохранения энергии
где E – полная механическая энергия тела (Дж); Ep т – потенциальная энергия взаимодействия тела и земли (Дж); Ep у – потенциальная энергия деформированной пружины (Дж); Ek – кинетическая энергия тела (Дж).
Задачи на применение закона сохранения энергии решайте, придерживаясь следующего плана:
- Сделайте схематический чертеж. Материальную точку изобразите в виде прямоугольника (или окружности). Укажите начальное и конечное положение тела, его скорость, нулевую высоту отсчета потенциальной энергии взаимодействия тела с землей.
- Запишите формулы для расчета полной механической энергии тела в начальном и конечном состоянии:
-
E0 = Ep т0 + Ep у0 + Ek0 , -
E = Ep т + Ep у + Ek .
-
- Если система замкнута, запишите закон сохранения механической энергии для данного случая:
-
E0 = E .
-
- Решите полученное уравнение. При необходимости выразите энергии через величины от которых они зависят.
- Индексы скоростей, высот, длин на рисунке должны соответствовать индексам скоростей, высот, длин в условии.
Закон об изменении механической энергии
- Закон об изменении механической энергии.
Работа внешних сил Aвн = ΔE = Е – E0, где Е и E0 – полные механические энергии системы в конечном и начальном состояниях соответственно.
Столкновение тел
При абсолютно неупругом ударе сохраняется только импульс, кинетическая энергия не сохраняется. Часть механической энергии при абсолютно неупругом ударе переходит во внутреннюю энергию, т.е. E0 – Е = Q.
При абсолютно упругом ударе сохраняется и импульс и механическая (кинетическая) энергия.