Решение. Графики. C1
Условие
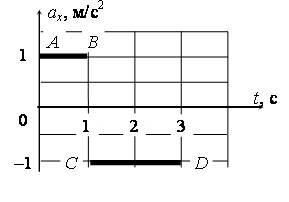
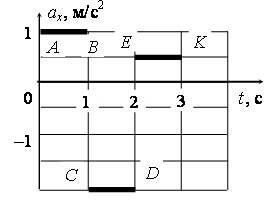
C1. По графикам зависимости ax(t), приведенным на рисунке 1 а и б, постройте графики зависимости υx(t), считая, что в начальный момент времени (t = 0) скорость движения материальной точки равна нулю.
Решение
а) Уравнение скорости в общем виде для участка АВ: υx1 = υ0x1 + ax1·t1, где υ0x1 = 0 м/с (по условию); ax1 = 1 м/с2; t1 = t. Тогда υx1 = t. Заполним таблицу значений:
| υx, м/с |
|
|
|---|---|---|
| t, с |
|
|
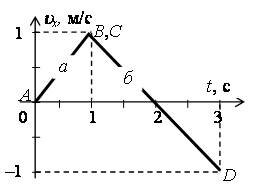
График представлен на рисунке 2 (линия а).
Для СD: υx2 = υ0x2 + ax2·t2, где υ0x2 = υx1(1 с) = 1 м/с; ax2 = –1 м/с2; t2 = t – 1 (второй участок отстает от первого на 1 с). Тогда υx2 = 2 – t. Заполним таблицу значений:
| υx, м/с |
|
|
|---|---|---|
| t, с |
|
|
График представлен на рисунке 2 (линия б).
б) Уравнение скорости в общем виде для участка АВ: υx1 = υ0x1 + ax1·t1, где υ0x1 = 0 м/с (по условию); ax1 = 1 м/с2; t1 = t. Тогда υx1 = t. Заполним таблицу значений:
| υx, м/с |
|
|
|---|---|---|
| t, с |
|
|
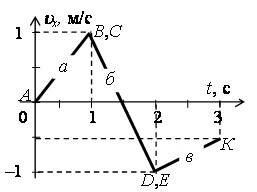
График представлен на рисунке 3 (линия а).
Для СD: υx2 = υ0x2 + ax2·t2, где υ0x2 = υx1(1 с) = 1 м/с; ax2 = –2 м/с2; t2 = t – 1 (второй участок отстает от первого на 1 с). Тогда υx2 = 3 – 2t. Заполним таблицу значений:
| υx, м/с |
|
|
|---|---|---|
| t, с |
|
|
График представлен на рисунке 3 (линия б).
Для ЕК: υx3 = υ0x3 + ax3·t3, где υ0x3 = υx2(2 с) = –1 м/с; ax3 = 0,5 м/с2; t3 = t – 2 (третий участок отстает от первого на 2 с). Тогда υx2 = –2 + 0,5t. Заполним таблицу значений:
| υx, м/с |
|
|
|---|---|---|
| t, с |
|
|
График представлен на рисунке 3 (линия в).