Решение. Графики. C3
Условие
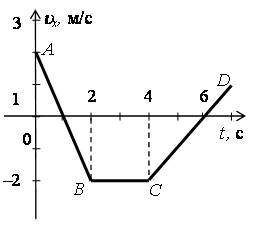
C3. По графику скорости, изображенному на рисунке 1, постройте график перемещения.
Решение
Уравнение перемещения в общем виде для участка АВ\[~\Delta r_{x1} = \upsilon_{0x1} \cdot t_1 + \frac{a_{x1} \cdot t^2_1}{2}\] , где υ0x1 = 2 м/с; \(~a_{x1} = \frac{\upsilon_{x2} - \upsilon_{x1}}{t^\prime_2-t^\prime_1};\) ax1 = –2 м/с2; t1 = t. Тогда \(\Delta r_{x1} = 2t - t^2\) . Заполним таблицу значений:
| Δrx1,м |
|
|
|
|
|
|---|---|---|---|---|---|
| t, с |
|
|
|
|
|
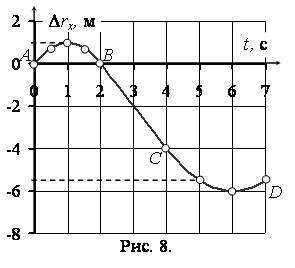
График представлен на рисунке 2 (линия АВ).
ВC\[~\Delta r_{x2} = \Delta r_{0x2} + \upsilon_{0x2} \cdot t_2 + \frac{a_{x2} \cdot t^2_2}{2}\] (ОБРАТИТЕ ВНИМАНИЕ: тело от начала движения уже совершило перемещение Δr0x2), где Δr0x2 = Δrx1(2 с) = 0 м; υ0x2 = –2 м/с; ax2 = 0 м/с2; t2 = t – 2 (второй участок отстает от первого на 2 с). Тогда \(\Delta r_{x2} = 4 - 2t\) . Заполним таблицу значений:
| Δrx2,м |
|
|
|---|---|---|
| t, с |
|
|
График представлен на рисунке 2 (линия ВС).
CD\[~\Delta r_{x3} = \Delta r_{0x3} + \upsilon_{0x3} \cdot t_3 + \frac{a_{x3} \cdot t^2_3}{2}\] , где Δr0x3 = Δrx2(4 с) = –4 м; υ0x3 = –2 м/с; ax3 = 1 м/с2; t3 = t – 4 (второй участок отстает от первого на 4 с). Тогда \(\Delta r_{x3} = 0,5t^2 - 6t + 12\) . Заполним таблицу значений:
| Δrx3,м |
|
|
|
|
|
|---|---|---|---|---|---|
| t, с |
|
|
|
|
|
График представлен на рисунке 2 (линия CD).