Решение. Равноускоренное движение. B5
Условие
B5. Ножной тормоз грузового автомобиля считается исправным если при торможении автомобиля, движущегося со скоростью 30 км/ч по сухой и ровной дороге, тормозной путь не превышает 9,0 м. Найдите соответствующее этой норме тормозное ускорение.
Решение
При прямолинейном движении путь автомобиля равен перемещению s = Δr. Тормозной путь – это расстояние, которое проходит автомобиль до остановки, следовательно, υ = 0.
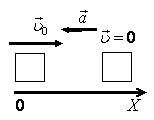
Используются величины Δrx, υ0x, υx и ax, нет t. Поэтому воспользуемся уравнением \(~\Delta r_x = \frac{\upsilon^2 _x + \upsilon^2 _{0x}}{2a_x}\) , где Δrx = s = 9,0 м; υx = 0; υ0x = υ0 = 30 км/ч ≈ 8,3 м/с (рис. 1). Тогда \(~s = \frac{-\upsilon^2 _0}{2a_x} ; a_x = -\frac{\upsilon^2 _0}{2s}\) ; ax ≈ –3,9 м/с2. Так как ax < 0, то ускорение направлено против выбранной оси.