Слободянюк А.И. Физика 10/1.1
§1. Описание положения тела в пространстве
1.1. Декартовые координаты точки в пространстве
Положение (место) точки в пространстве математически удобно описывать с помощью чисел – координат. Простейшей системой (и хорошо вам знакомой) координат является прямоугольная декартовая система. Для ее построения необходимо задать (см. рис.1):
- Начало отсчета – произвольную точку O;
- Направления трех взаимно перпендикулярных осей координат, традиционно обозначаемых (X, Y, Z);
- Единицу измерения длины (отрезок единичной, по определению, длины).
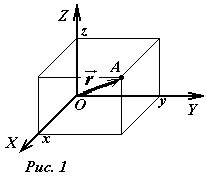
Для определения координат точки A необходимо опустить перпендикуляры из точки A на оси координат (спроецировать точку на оси координат) и задать координаты точек-проекций (x,y,z). Каждое число-координата имеет следующий смысл: декартовой координатой точки на прямой является число, модуль которого равен расстоянию до начала отсчета, а знак указывает, с какой стороны от начала отсчета находится данная точка.
Так как координата точки указывает расстояние до начала отсчета, то ее размерность - размерность длины.
Рассмотрим теперь эти известные математические положения с физической точки зрения. Пространство, в котором мы живем, не имеет «выделенных» точек и направлений, с которыми раз и навсегда можно связать единую и абсолютную систему отсчета. Поэтому положение данного тела можно определить только относительно других тел. В связи с этим начало отсчета физической системы координат удобно связывать с некоторым конкретным телом (которое называется тело отсчета). Направления осей координат также следует связывать с другими материальными телами. В качестве единицы длины используются эталоны, которые воспроизводятся с помощью физических приборов. В международной системе единиц СИ единицей длины является метр.
Подчеркнем, что выбор всех элементов системы координат, в принципе, является произвольным, следовательно, координаты точки относительны. Иными словами, числа-координаты имеют смысл только в том случае, если задана система координат, то есть положение данного тела определяется относительно других тел, с которыми связана система координат.
Во многих случаях задание трех координат точки является излишним. Так если тело движется вдоль заданной (известной) прямой, то имеет смысл одну из осей (скажем X) направить вдоль этой прямой. Тогда оставшиеся координаты (y,z) все время будут равны нулю, поэтому их можно не принимать во внимание.
Заметим, что аналогичным образом можно ввести координаты точки на произвольной заданной линии, измеряя длину участка этой линии между данной точкой и началом отсчета и указывая с помощью знаков с какой стороны от начала отсчета находится точка.
Аналогично, при движении тела по заданной плоскости (и даже произвольной поверхности), достаточно определить в этой плоскости две оси координат.
Эквивалентным координатному является векторный способ описания положения.
В рамках этого метода положение точки в пространстве задается с помощью радиус-вектора \(~\vec r\) , вектора, соединяющего начало координат с рассматриваемой точкой. Координатами этого вектора являются декартовые координаты точки (x,y,z).
Смотреть HD
видео онлайн
бесплатно 2022 года
