Слободянюк А.И. Физика 10/1. Описание положения тела в пространстве.

Материал из PhysBook

Перейти к: навигация, поиск

Содержание

1 Описание положения тела в пространстве
2 Примечания

Описание положения тела в пространстве

Декартовые координаты точки в пространстве

Положение (место) точки в пространстве математически удобно описывать с помощью чисел – координат. Простейшей системой (и хорошо вам знакомой) координат является прямоугольная декартовая система. Для ее построения необходимо задать (см. рис.1):

Начало отсчета – произвольную точку O;
Направления трех взаимно перпендикулярных осей координат, традиционно обозначаемых (X, Y, Z);
Единицу измерения длины (отрезок единичной, по определению, длины).

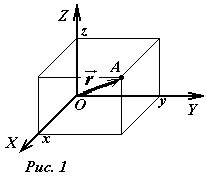
Для определения координат точки A необходимо опустить перпендикуляры из точки A на оси координат (спроецировать точку на оси координат) и задать координаты точек-проекций (x,y,z). Каждое число-координата имеет следующий смысл: декартовой координатой точки на прямой является число, модуль которого равен расстоянию до начала отсчета, а знак указывает, с какой стороны от начала отсчета находится данная точка.

Так как координата точки указывает расстояние до начала отсчета, то ее размерность - размерность длины.

Рассмотрим теперь эти известные математические положения с физической точки зрения. Пространство, в котором мы живем, не имеет «выделенных» точек и направлений, с которыми раз и навсегда можно связать единую и абсолютную систему отсчета. Поэтому положение данного тела можно определить только относительно других тел. В связи с этим начало отсчета физической системы координат удобно связывать с некоторым конкретным телом (которое называется тело отсчета). Направления осей координат также следует связывать с другими материальными телами. В качестве единицы длины используются эталоны, которые воспроизводятся с помощью физических приборов. В международной системе единиц СИ единицей длины является метр.

Подчеркнем, что выбор всех элементов системы координат, в принципе, является произвольным, следовательно, координаты точки относительны. Иными словами, числа-координаты имеют смысл только в том случае, если задана система координат, то есть положение данного тела определяется относительно других тел, с которыми связана система координат.

Во многих случаях задание трех координат точки является излишним. Так если тело движется вдоль заданной (известной) прямой, то имеет смысл одну из осей (скажем X) направить вдоль этой прямой. Тогда оставшиеся координаты (y,z) все время будут равны нулю, поэтому их можно не принимать во внимание.

Заметим, что аналогичным образом можно ввести координаты точки на произвольной заданной линии, измеряя длину участка этой линии между данной точкой и началом отсчета и указывая с помощью знаков с какой стороны от начала отсчета находится точка.

Аналогично, при движении тела по заданной плоскости (и даже произвольной поверхности), достаточно определить в этой плоскости две оси координат.

Эквивалентным координатному является векторный способ описания положения.

В рамках этого метода положение точки в пространстве задается с помощью радиус-вектора $~\vec r$ , вектора, соединяющего начало координат с рассматриваемой точкой. Координатами этого вектора являются декартовые координаты точки (x,y,z).

Преобразования координат

Как уже было отмечено, координаты точки относительны, они изменяются при переходе в другую систему координат. Во многих случаях, требуется перейти из одной системы координат в другую. Получим формулы таких преобразований для одного частного случая – сдвига начала отсчета на плоскости. Пусть на известной плоскости заданы две декартовые системы координат XOY (которую условно назовем «исходной») и X’O’Y’ (назовем ее «сдвинутой»), оси которых параллельны (см. рис.2). Обозначим (x₀,y₀) координаты начала отсчета сдвинутой системы в исходной системе.

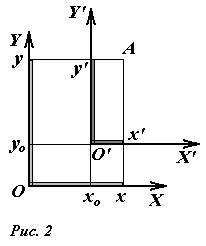
Как следует из рис. 2, координаты точки A в сдвинутой и исходной системах связаны очевидными соотношениями (прямые)

$~\begin{cases} x' = x - x_0 \\ y' = y - y_0 \end{cases}$ , (1)

обратные:

$~\begin{cases} x = x' + x_0 \\ y = y' + y_0 \end{cases}$ . (2)

Какую из этих систем считать исходной, а какую сдвинутой, безразлично – системы полностью равноправны. Заметьте, что обратные преобразования могут быть получены заменой (x₀,y₀) на (-x₀,-y₀) . Последняя пара чисел является координатами начала отсчет исходной системы в сдвинутой.

Эти же преобразования короче могут быть записаны и в векторной форме (рис. 3)

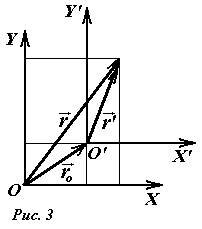
$~\vec r^\prime = \vec r - \vec r_0 ; \vec r = \vec r^\prime + \vec r_0$ . (3)

Аналогичные преобразования при параллельном сдвиге начала отсчета могут быть получены и в трехмерном случае. Более сложный вид имеют формулы преобразования координат при повороте осей (в нашем изложении они нам не понадобятся, поэтому приводить их не будем). Важно, что в любом случае можно найти формулы, позволяющие переходить из одной системы координат в другую. Это обстоятельство, указывает, что произвол в выборе системы координат не вносит существенных трудностей в описание движения тел.

Относительные и инвариантные величины

Мы показали, что при переходе из одной системы в другую координаты точки изменяются (координаты относительны). Помимо относительных величин (зависящих от системы координат) имеются величины независящие от системы координат (такие величины называются инвариантными). Примером такой величины является расстояние между двумя точками. Действительно, пусть на плоскости (рис.4) расположены две точки: A₁ с координатами (x₁,y₁) и A₂ с координатами (x₂,y₂).

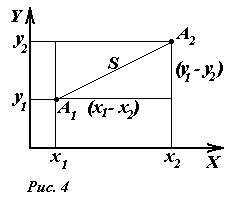
Тогда на основании теоремы Пифагора расстояние между точками может быть вычислено по формуле

$~s = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}$ . (4)

При переходе в любую другую систему отсчета (при неизменной единице длины) расстояние, вычисленное по формуле (4), остается неизменным. Например, при сдвиге начала отсчета, описываемом уравнениями (1), все четыре координаты изменятся, но разности одноименных координат, а, следовательно, и расстояние останутся неизменными (инвариантными). Можно указать и другие геометрические инвариантные величины – углы между отрезками, площади и объемы фигур и др. Особенно отметим, что соотношения, записанные в векторной форме, остаются неизменными при преобразованиях координат. Так, например, скалярное произведение^[1] двух векторов не зависит от выбора системы координат. В частном случае, скалярное произведение вектора на самого себя равно квадрату длины вектора. Поэтому формула (4) в векторной форме имеет вид

$~s = \sqrt{(\vec r_1 - \vec r_2) \cdot (\vec r_1 - \vec r_2)}$ . (4a)

Поиск инвариантных величин, не изменяющихся при преобразованиях координат, представляет большой интерес, а многие физические теории и формулируются в терминах инвариантных величин.

Задание для самостоятельной работы

1. В полярной системе координат положение точки A на плоскости задается с помощью а) расстояния r до начала координат O, б) угла φ, который образует отрезок OA с осью X.

Установите связь между полярными (r,φ) и декартовыми координатами точки.

Выразите расстояние между двумя точками через их полярные координаты.

Обсуждая вопрос об описании положения тела в пространстве, мы стыдливо умолчали о том, что не определили понятия «тело». Фактически речь шла о геометрических точках пространства. Любой реальный объект имеет конечные геометрические размеры и определенную форму. Кроме того, реальные тела обладают множеством иных характеристик - массой, температурой, цветом и так далее. Полностью описать все свойства реальных тел, все физические процессы в рассматриваемых телах невозможно из-за их бесконечного многообразия. Поэтому, рассматривая те или иные явления необходимо отвлечься, «забыть» на время, пренебречь некоторыми характеристиками тел и явлений, иными словами, построить модель явления, модель тела. Какими свойствами тела можно в данных условиях пренебречь зависит от конкретной физической задачи, конкретной цели физического исследования.

Материальная точка

Во многих кинематических задачах оказывается возможным пренебречь размерами самого тела. Еще раз рассмотрим автомобиль, движущийся из Минска в Брест. Расстояние между этими городами порядка 350 километров, размеры автомобиля - несколько метров, поэтому в такой ситуации при описании положения автомобиля можно не учитывать его размеры - если капот автомобиля находится в Бресте у нужного подъезда нужного дома, то можно считать, что и его багажник находится приблизительно там же. Таким образом, в данной задаче можно мысленно заменить автомобиль его моделью - телом, размеры которого пренебрежимо малы. Такая модель тела очень часто используется в физике и называется материальной точкой.

Материальная точка - это идеальная модель тела, размерами которого в данных условиях можно пренебречь.

Общим у геометрической и материальной точек является отсутствие собственных размеров. Материальную точку, по мере необходимости, можно «наделять» свойствами, которыми обладают реальные тела, например, массой, энергией, электрическим зарядом и так далее.

Одним из критериев применимости модели материальной точки является малость размеров тела по сравнению с расстоянием, на которое оно перемещается. Однако это условие не является абсолютно однозначным. Так, описывая движение Земли вокруг Солнца при расчете ее положения на орбите, размерами Земли можно пренебречь, считать ее материальной точкой. Однако, если нам необходимо рассчитать времена восхода и заката Солнца, модель материальной точки принципиально неприменима, так как это описание требует учета вращения Земли, учета ее размеров и формы.

Рассмотрим еще один пример. Спринтеры соревнуются на стометровой дистанции. Цель описания движения – выявить, кто из спортсменов пробегает дистанцию за меньшее время (задача чисто кинематическая). Можно ли в данной задаче считать бегуна материальной точкой? Его размеры значительно меньше дистанции забега, но достаточно ли они малы, чтобы ими можно было пренебречь? Ответ на эти вопросы зависит от требуемой точности описания. Так, на серьезных соревнованиях время измеряется с точностью 0.01 секунды, за это время бегун смещается на расстояние порядка 10 сантиметров (простая оценка, полученная исходя из средней скорости спринтера 10м/с). Следовательно, погрешность, с которой определяется положением бегуна (10 см) меньше, чем его поперечные размеры, поэтому модель материальной точки в данном случае неприменима. Не случайно мастера спринтерского бега на финише «бросают грудь вперед», выигрывая драгоценные сотые доли секунды. Таким образом, вторым критерием применимости модели является требуемая точность описания физического явления.

В некоторых ситуациях можно использовать модель материальной точки, даже если размеры тела сравнимы и даже больше расстояний, на которое смещается тело. Это допустимо тогда, когда положение одной точки тела однозначно определяет положение всего тела. Так при скольжении бруска по наклонной плоскости, зная положение его центра (как, впрочем, и любой другой точки) можно найти положение всего тела. Если модель материальной точки оказывается неприменимой, то необходимо использовать другие более сложные модели.

Абсолютно твердое тело

Многие реальные тела являются твердыми, то есть в течении длительного времени сохраняют свои размеры и форму, точнее говоря изменения размеров и формы настолько незначительны, что ими можно пренебречь. Моделью таких тел служит абсолютно твердое тело.

Абсолютно твердое тело - это идеальная модель тела, изменением размеров и формы которого в данных условиях можно пренебречь.

Из этого определения следует, что расстояния между двумя любыми точками абсолютно твердого тела остается неизменным. Абсолютно твердое тело можно также рассматривать как совокупность материальных точек, жестко связанных между собой. Так положение океанского лайнера в открытом море можно описать, пользуясь моделью материальной точки, а его пространственную ориентацию (курс, наклон) с помощью модели абсолютно твердого тела. Применимость модели абсолютно твердого тела обусловлена только конкретной исследуемой проблемой - целью моделирования и требуемой точностью.

Число степеней свободы тела

Теперь, после того как мы изучили несколько моделей тел, можно окончательно и корректно сформулировать ответ на вопрос: «Что означает задать, определить положение тела?» - Указать численной значение координат некоторых точек тела так, чтобы положение всего тела (любой его части) было определено однозначно.

Число независимых координат, которые однозначно определяют положение тела или системы тел в пространстве называется числом степеней свободы.

Число степеней свободы очень важная характеристика описываемой системы, хотя бы потому, что определяет число независимых уравнений, описывающих движение системы.

Подсчитаем число степеней свободы некоторых простых систем.

Материальная точка, по определению, не имеет размеров, поэтому ее положение в пространстве определяется однозначно тремя координатами. Следовательно, число степеней свободы свободно материальной точки равно трем. Если на движение материальной точки накладываются дополнительные условия, то число ее степеней свободы может уменьшиться. Так если точка движется по заданной поверхности, то ее положение определяется двумя независимыми координатами, следовательно, число степеней свободы равно двум; при движении по заданной линии число степеней свободы уменьшается до одной. Подчеркнем, это не значит, что при движении по заданной линии может изменяться только одна и - могут изменяться все три, но положение точки на заданной линии определяется одной координатой, и если она известна, то могут быть определены и две других. Тем не менее, описание положения точки на заданной линии с помощью одной координаты оказывается не всегда удобным. Ценность рассмотренных нами декартовых координат в том, что они позволяют установить физические законы, описывающее движение вдоль всех прямых (все прямые одинаковы!). В то же время, для описания изменения координат на произвольной линии пришлось бы записывать свои законы для каждой линии - окружности, параболы, синусоиды и т.д. Поэтому часто одномерное движение вдоль известной линии описывают с помощью двух или трех координат. Однако и в этом случае число степеней свободы остается равным единице.

Если механическая система может быть промоделирована как N материальных точек, движущихся в пространстве, то, очевидно, полное число ее степеней свободы равняется 3N. Но если на движение этих материальных точек накладываются дополнительные ограничения, то число степеней свободы уменьшается.

Рассмотрим, как можно описать положение в пространстве двух материальных точек жестко связанных между собой (что-то похожее на гантели). Две точки имеют шесть степеней свободы, которые могут быть описаны шестью координатами - x₁, y₁, z₁, x₂, y₂, z₂, но так как расстояние между точками неизменно, то на эти координаты накладывается условие

$~(x_1 - x_2)^2 + (y_1 - y_2)^2 + (z_1 - z_2)^2 = l^2$ ,

где l - расстояние между точками, поэтому число независимых координат, или число степеней свободы равно пяти.

Таким образом, число степеней свободы системы, состоящей из N материальных точек равно 3N минус число дополнительных условий (связей), накладываемых на движение этих точек.

Число степеней свободы может быть подсчитано и другим способом. Обратим внимание, что точное определение координат уменьшает «подвижность» точки (или системы точек). Так, например, если для материальной точки задана координата z, то точка может двигаться только в плоскости перпендикулярной оси Z, задание еще одно координаты (скажем y), приводит к тому, что точка может двигаться только вдоль прямой параллельной оси X. Поэтому число степеней свободы можно находить, подсчитывая, сколько независимых координат необходимо определить, чтобы жестко «закрепить» тело. С помощью такого подхода найдем число степеней свободы системы, состоящей из двух жестко связанных точек. Задавая три координаты одной точки, мы ее как бы закрепляем, тогда вторая точка сможет двигаться так, что бы ее расстояние до первой оставалось неизменным, то есть по поверхности сферы радиуса l. Понятно, что если определено положение двух точек твердого тонкого стержня, то задано и положение всего стержня, поэтому тонкий стержень имеет пять степеней свободы.

Посчитаем число степеней свободы свободно движущегося абсолютно твердого тела. Выберем внутри тела три произвольных точки A, B, C, не лежащих на одной прямой. (рис 5). Положение одной точки A, определяется тремя координатами, если задано положение точки A, то положение точки B может быть описано двумя координатами. Наконец, при «закрепленных» точках A и B, тело может только вращаться вокруг оси, проходящей через эти точки. Следовательно, точка C имеет одну степень свободы. Таким образом, абсолютно твердое тело имеет шесть степеней свободы.

Как мы уже отмечали, для описания положения точки можно использовать разные системы координат, аналогично, положение твердого тела также может быть описано различными способами, только число независимых координат во всех способах описания будет одним и тем же равным числу степеней свободы. Так во многих случаях, положение твердого тела, описывают, задавая три декартовые координаты одной из его точек (чаще центра), и три угла, определяющие его ориентацию.

Существует ли четвертое измерение?

В научно-фантастических произведения иногда встречаются сюжеты, в которых разумные существа осваивают четвертое, пятое и так далее измерения ^[2]. Повышение размерности пространства предоставляет новые богатейшие возможности, как для этих существ, так и для писателей-фантастов. Сравните двухмерную плоскость и трехмерное пространство! Для того чтобы «выйти» из плоскости в трехмерное пространство можно предложить следующий метод: из центра окружности необходимо провести бесконечный луч, который нигде не пересекает окружность, такой луч лежит в третьем измерении. По аналогии можно предложить «путь в четвертое измерение»: из центра сферы необходимо провести луч, который нигде не пересекает сферу - вообразили? Еще один способ - провести прямую, которая перпендикулярна трем взаимно перпендикулярным прямым. Конечно, если вам не удалось представить себе такой луч или такую прямую, то это еще не является доказательством отсутствия четвертого измерения в нашем пространстве.

Попытаемся представить, к каким наблюдаемым явлениям могло бы привести наличие дополнительного измерения. Например, «из четвертого измерения» можно было бы заглянуть внутрь любого трехмерного тела (как из третьего измерения можно видеть «внутренности» любой плоской фигуры). Далее, был бы возможен бесследный «уход» и обратное появление в любом другом месте любых материальных тел (опять же представьте себе, что будет происходить на плоскости, которую пересекает трехмерное тело). К настоящему времени таких фактов не зафиксировано. Более того, не известно таких явлений, которые не могли бы быть объяснены с точки зрения пространства трех измерений.

Еще одним доказательством трехмерности пространства, в котором мы обитаем, является ряд физических законов. Рассмотрим, например, точечный источник, который посылает свет во все стороны равномерно. Понятно, что энергия, пересекающая поверхность любой сферы, внутри которой находится источник, должна быть постоянна. Следовательно, интенсивность света (то есть энергия, приходящаяся на единицу площади) должна убывать обратно пропорционально площади сферы, то есть обратно пропорционально квадрату расстояния. Если бы свет распространялся и в четвертом измерении, то его интенсивность убывала бы обратно пропорционально кубу расстояния. Эксперимент однозначно утверждает, что интенсивность убывает обратно пропорционально квадрату расстояния. Эти и другие факты утверждают, что наше пространство действительно трехмерно. Таким образом, ответ на вопрос этого раздела в настоящее время следующий:

Пространство четырех и более измерений является математической абстракцией, можно изучать свойства геометрических объектов в таких пространствах, при решении целого ряда задач, в том числе физических бывает полезно их рассматривать в многомерных пространствах, однако, в настоящее время нет никаких оснований полагать, что реально существует четвертое измерение в том смысле, что реально существуют некоторые материальные тела вне пространства трех измерений.

Вопросы для самостоятельной работы.

Подсчитайте число степеней свободы тонкого стержня, толщиной которого можно пренебречь.
Две материальные точки связаны пружиной. Чему равно число степеней свободы такой системы?
Чему равно число степеней свободы руки человека?

Механическое движение. Закон движения

Окружающий нас мир не является застывшим, в нем постоянно происходят всевозможные изменения - «все течет, все изменяется», и нет необходимости убеждать кого-либо в этой очевидной истине. Простейшим видом изменений, происходящих в окружающем нас мире, является изменение положений тел в пространстве, механическое движение.

Механическим движением называется изменение положений тел в пространстве с течением времени.

При движении материальной точки она описывает в пространстве некоторую линию. Для описания движения можно попытаться найти эту линию, а затем описывать положение точки на этой ней. Для этого можно, например, задать зависимость пройденного пути от времени движения.

Линия, вдоль которой движется материальная точка, называется траекторией движения.

Путь, пройденный точкой равен длине участка траектории между двумя последовательными положениями тела.

Однако определение траектории движения часто представляет собой отдельную и достаточно сложную задачу, поэтому часто оказывается более простым и удобным описывать механическое движение иным способом.

Мы уже знаем, что положение тела в пространстве описывается с помощью координат. Если положение тела изменяется, то изменяются и его координаты, они становятся зависящими от времени, становятся функциями времени.

Зависимость всех координат тела от времени называется законом движения.

Таким образом, закон движения определяет положение тела в любой произвольный момент времени. Математическим выражением закона движения является набор функций - зависимостей координат от времени. Таким образом, нам необходимо дополнить рассмотренную систему координат прибором для измерения времени - часами. Дальше такой набор - системы координат и часов мы будем называть системой отсчета. Как всякая функция закон движения может быть представлен в нескольких формах - в виде таблицы, в виде графика, в виде формулы.

Подчеркнем, что закон движения полностью описывает движение, дает исчерпывающую информацию о движении, зная его можно найти любую характеристику движения. Однако, задача физики, заключается не только в том чтобы просто описать наблюдаемое движение, более важная задача - научиться предсказывать движение, рассчитывать его, строить его модели, создавать условия, для того чтобы получить движение требуемого вида. Для успешного решения таких проблем нам необходимо ввести и изучить некоторые характеристики механического движения (скорость, ускорение и т.д.), которые позволяют теоретически находить законы движения.

Примечания

↑ Напомним, результатом скалярного произведения двух векторов $~\vec A$ и $~\vec B$ называется число c , равное произведению модулей векторов на косинус угла α между ними: $~c = \vec A \cdot \vec B = |\vec A| \cdot |\vec B| \cdot \cos \alpha$ .
↑ Для примера можно вспомнить знаменитый роман М.Булгакова «Мастер и Маргарита»