Слободянюк А.И. Физика 10/11.12
§11. Постоянный электрический ток
11.12 Закон Ома для полной цепи.
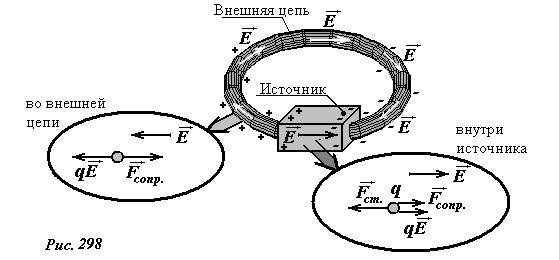
Рассмотрим подробнее процессы, протекающие в замкнутой цепи электрического тока, содержащей источник (рис. 298).
Внутри источника под действием сторонних сил начинается разделение зарядов: положительно заряженные частицы движутся к положительному полюсу источника, а отрицательные частицы к отрицательному. Разделенные заряды создают внутри источника электрическое поле \(~\vec E\) , направленное от «плюса» к «минусу», которое препятствует дальнейшему движению зарядов. Кроме того, на движущиеся заряженные частицы действуют силы сопротивления среды Fsopr. Чтобы заряженные частицы продолжали двигаться, к ним должна быть приложена сторонняя сила Fst. При постоянном токе (в установившемся режиме) соотношение между действующими силами очевидно – сумма сил, действующих на частицу должна быть равна нулю, или
Работа сторонних сил по перемещению единичного положительного заряда, по определению равна ЭДС источника ε. Работа сил сопротивления отрицательна и по модулю равна произведению силы тока на внутреннее сопротивление источника Ir. Работа сил электрического поля при движении зарядов внутри источника также отрицательна.
При подключении внешней цепи внутри проводника возникает электрическое поле. Механизм создания этого поля достаточно сложен. Несколько упрощенно можно сказать, что на поверхности проводника появляются заряды, распределение которых таково, что они создают внутри проводника такое электрическое поле [1], которое поддерживает постоянный по всей цепи электрический ток.
Подобно тому, как в электростатике индуцированные заряды и электрическое поле приходят в равновесие, при котором прекращается движение зарядов, в случае постоянного тока наступает равновесие несколько иного вида – постоянство электрического тока. Если в каком то месте электрический ток превышает равновесное значение, то происходит накопление заряда, которое уменьшает электрический ток, и наоборот при недостатке зарядов в некоторой области цепи, увеличивающийся электрический ток компенсирует недостаток заряда.
Во внешней цепи заряженные частицы движутся под действием силы со стороны созданного электрического поля, которая при постоянном токе равна силе сопротивления
Во внешней цепи работа электрического поля по перемещению зарядов положительна (и для единичного заряда равна разности потенциалов на концах внешней цепи), а работа сил сопротивления по-прежнему отрицательна и равна по модулю произведению силы тока на сопротивление цепи IR.
Проследим за движением отдельной заряженной частицы по всему контуру – совершив полный обход, эта частица возвращается в исходное состояние. Следовательно, ее энергия также принимает начальное значение. Поэтому полная работа внешних сил, при движении частицы по замкнутому контуру равна нулю. Во время движения на рассматриваемую частицу действовали силы сопротивления, сторонние силы и силы электростатического поля.
Но, электростатическое поле всегда потенциально, поэтому работа этих сил по контуру равна нулю – положительная работа во внешней цепи равна по модулю отрицательной работе внутри источника Ael = 0. Поэтому при движении по контуру работа сторонних сил равна по модулю работе сил сопротивления Ast + Asopr. Для единичного заряда это утверждение выражается уравнением
из которого следует, что сила тока в цепи рассчитывается по формуле
Сила тока в замкнутом контуре цепи равна отношению ЭДС контура к полному сопротивлению контура. Данное утверждение называется законом Г.С. Ома для полной цепи. Фактически данный закон можно рассматривать как закон сохранения энергии для системы движущихся зарядов. Действительно, энергия, сообщенная заряженной частице, равна работе по преодолению сил сопротивления. Если все потери энергии частицы обусловлены сопротивлением цепи, то указанная работа равна количеству теплоты, выделившейся во внешней цепи и внутри источника. Если в цепи имеются приборы, преобразующие энергию электрического тока в другие формы (механическую, световую, химическую и т.д.), то работа источника равна сумме энергии, потребляемой этими приборами, и количества теплоты, выделившейся в цепи – иными словами, закон сохранения энергии не знает исключений и в данных явлениях.
Примечания
- ↑ Мы не утверждаем, что напряженность этого поля равна напряженности поля внутри источника, более того, электрические поля могут быть различны в различных точках как внутри источника, так и во внешней цепи.