Слободянюк А.И. Физика 10/15.2
§15. Переменное электромагнитное поле
15.2 Ток смещения.
Если переменное магнитное поле создает поле электрическое, то разумно предположить существование и обратного процесса: изменяющееся электрическое поле порождает поле магнитное. Такое явление действительно существует и носит не совсем обычное название ток смещения[1], его происхождение мы поясним в конце данного раздела.
Весьма интересна история открытия этого явления. Впервые предсказал существование такого процесса М. Фарадей вместе с открытием электромагнитной индукции. Последователь Фарадея, его соотечественник Дж. К. Максвелл в 1873 году даже дал теоретическое описание этого явления, написав уравнения которые позволяют рассчитать характеристики индуцированного магнитного поля. Экспериментально же это явление было открыто и исследовано значительно позднее.
Дж. К. Максвелл пришел к выводу этого закона из теоретических рассуждений, которые потребовали изменения теоремы о циркуляции вектора индукции магнитного поля в случае переменных полей.
Стационарные магнитные поля создаются постоянными электрическими токами (или, что равносильно, движущимися зарядами). Индукция стационарного магнитного поля рассчитывается по закону Био-Савара, который подтверждается многочисленными экспериментальными данными, поэтому сомнений в его справедливости не возникает. Эквивалентной формулировкой этого закона является теорема о циркуляции магнитного поля: циркуляция вектора индукции равна сумме токов, пересекающих любую поверхность, натянутую на контур, умноженной на магнитную постоянную
Распространение этой теоремы (соответственно и закона Био-Савара) на изменяющиеся во времени поля приводит к серьезному противоречию.
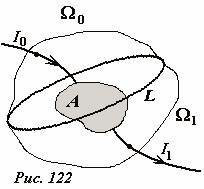
Пусть к проводящему телу A подключены два провода, по которым протекают электрические токи (Рис. 122) Выберем произвольный контур L, не пересекающий данное тело. Построим две поверхности, опирающиеся на данный контур: Ω0, которую пересекает проводник с током I0, и Ω1, которую пересекает проводник с током I1. Из уравнения (1) следует, что для поверхности Ω0 циркуляция равна μ0I0, а для поверхности Ω1 - μ0I1. То есть обязательно должно выполняться условие I0 = I1. В стационарном режиме это равенство является выражением закона сохранения электрического заряда. Применение теоремы о циркуляции в такой форме «на все случаи жизни» приводит к парадоксальному выводу: невозможно зарядить никакое тело?!
В действительности электрический заряд может накапливаться на проводнике A, поэтому силы токов в проводниках могут различаться, в частности, ток I1 может вообще отсутствовать. Принципиальная особенность процесса зарядки (или разрядки) заключается в том, что изменяется электрический заряд тела, и как следствие изменяется электрическое поле. Поэтому Дж. К. Максвелл и высказал гипотезу, что изменяющееся электрическое поле создает магнитное поле.
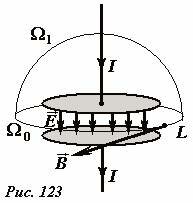
Для установления связи между характеристиками этих полей, рассмотрим процесс зарядки плоского конденсатора, образованного двумя круглыми параллельными пластинами, которые заряжаются посредством электрических токов, протекающих по прямым проводам, расположенных на оси конденсатора (Рис. 123). Выберем контур в виде окружности L, плоскость которой перпендикулярна оси системы, центр ее также находится на этой оси. Во всех точках этой окружности существует магнитное поле, которое создается, по крайней мере, электрическими токами в проводах. Это поле, также как и вся система обладает осевой симметрией, поэтому вектор индукции на рассматриваемом контуре постоянен по модулю и направлен по касательной к нему[2]. Следовательно, циркуляция вектора индукции по этому контуру равна произведению модуля вектора индукции на длину контура
Если в качестве поверхности, опирающейся на контур, выбрать полусферу Ω1, охватывающую пластину конденсатора, то ее пересекает проводник, по которому идет зарядка током силой I. Поэтому по теореме о циркуляции следует записать \(\Gamma_B = 2 \pi r B = \mu_0 I\), откуда следует, что величина индукции поля на рассматриваемом контуре равна \(~B = \frac{\mu_0 I}{2 \pi r}\), и совпадает с индукцией поля прямого проводника.
Если же в качестве поверхности, опирающейся на контур выбрать Ω0 - круг, лежащий в плоскости, параллельной пластинам, то его электрический ток не пересекает, в этом случае следует признать, что магнитное поле на рассматриваемом контуре отсутствует. Что бы избежать этого противоречия, Дж. К. Максвелл предложил дополнить выражение для циркуляции дополнительным слагаемым, зависящим от изменения электрического поля. На поверхности полусферы Ω1 электрическое поле отсутствует, поэтому для нее формула (1) справедлива. Поверхность Ω0 электрический ток не пересекает, но на этой поверхности существует электрическое поле. Вычислим поток вектора напряженности электрического поля. Если расстояние между пластинами значительно меньше их радиусов, то можно считать, электрическое поле существует только между обкладками и является однородным. Напряженность этого поля равна \(~E = \frac{\sigma}{\varepsilon_0}\), где σ - поверхностная плотность заряда на пластине. Поток этого вектора через поверхность Ω0 , равен \(~\Phi_E = E S = \frac{\sigma S}{\varepsilon_0} = \frac{q}{\varepsilon_0}\), где q - изменяющийся заряд пластины, S - ее площадь. Максвелл заметил, что скорость изменения этого потока пропорциональна силе тока, заряжающего это пластину
Если предположить, что произведение скорости изменения электрического потока на электрическую постоянную \(~\varepsilon_0 \frac{\Delta \Phi_E}{\Delta t}\) эквивалентно силе обычного тока проводимости (в том смысле, что создает такое же магнитное поле) и обобщить теорему о магнитном потоке, включив в нее это слагаемое, то выявленные противоречия снимаются.
Величину \(~\varepsilon_0 \frac{\Delta \Phi_E}{\Delta t}\) Дж. К. Максвелл назвал силой тока смещения, а само явление возникновения магнитного поля при изменении электрического поля – током смещения.
Рассматривая процесс зарядки конденсатора, заполненного диэлектриком, Максвелл пришел к выводу, что изменяющаяся поляризация диэлектрика, вызванная смещением (в обычном механическом смысле) связанных зарядов эквивалентна электрическому току. Затем этот термин был распространен и на изменяющееся поле в вакууме, где заряженные частицы отсутствуют, а их «смещение[3]» осталось.
В итоге Дж. К. Максвелл сформулировал теорему о циркуляции в обобщенном виде: Циркуляция вектора магнитной индукции по любому контуру равна сумме токов проводимости и токов смещения, пересекающих данную поверхность, умноженной на магнитную постоянную
Следует отметить, что приведенные рассуждения об обобщенной теореме о циркуляции, ни в коем случае не является ее выводом или доказательством. Реальное существование токов смещения (т.е. возникновения магнитного поля под действием поля электрического) подтверждается только результатами многочисленных экспериментов. Поэтому выводы Дж. К. Максвелла являются гениальными догадками и предсказаниями, экспериментально подтвержденными значительно позднее. Важнейшим доказательством существования рассматриваемого явления послужило открытие и исследование немецким физиком Г. Герцем в 1886-1889 годах электромагнитных волн, которые не могли бы существовать, если не существует токов смещения.
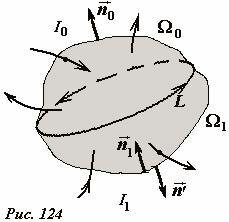
Покажем, что введение токов смещения приводит к уравнению, правильно описывающему изменение электрического заряда. Пусть произвольную замкнутую поверхность пересекают произвольные электрические токи. Выберем на этой поверхности замкнутую линию (контур) L, который разбивает ее на две части Ω0 и Ω1 (Рис. 124). Применим теорему о циркуляции к выделенному на данной поверхности контуру. Положительным направлением обхода контура будем считать, как обычно, направление «против часовой стрелки». Для произвольной поверхности, опирающейся на контур, положительное направление нормалей к поверхности определяется правилом правого винта (две такие нормали \(~\vec n_0\) , \(~\vec n_1\) показаны на рисунке). Применим теорему о циркуляции для контура L для двух введенных поверхностей, натянутых на этот контур
здесь I0, I1 - алгебраические суммы токов, пересекающие указанные поверхности, ФE0,ФE1 - потоки векторов напряженности электрического поля через эти же поверхности. Положительное направление электрического тока (и потока вектора напряженности) на каждой поверхности указывает вектор положительной нормали. Изменим теперь правило знаков: положительным будем считать ток, вытекающий из данного объема, то есть будем считать положительным ток, направление которого совпадает с направлением внешней нормали к замкнутой поверхности (Ω0 + Ω1). При таком определении сила токов, пересекающая поверхность Ω0 не изменится I’0 = I0 (аналогично Ф’E0 = ФE0). На поверхности Ω1 изменится на противоположное направление нормали, поэтому изменятся знаки суммы электрических токов и потока вектора напряженности I’1 = -I1, Ф’E1 = -ФE1. С учетом указанной замены равенство циркуляций (3) выражается уравнением
или
В этом уравнении (I’0 + I’1)= I - сила тока, вытекающего из данной поверхности, (Ф’E0 + Ф’E1) - поток вектора напряженности электрического поля через замкнутую поверхность, который по теореме Гаусса равен заряду внутри поверхности, деленному на электрическую постоянную \(~(\Phi'_{E0} + \Phi'_{E1}) = \frac{q}{\varepsilon_0}\). Таким образом, уравнение (4) приобретает простой вид I \(~\frac{\Delta q}{\Delta t} = -I\) и очевидный смысл: уменьшение заряда внутри замкнутой поверхности равно сумме электрических токов, вытекающих из этой поверхности.
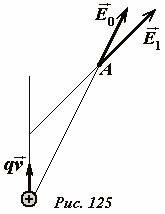
Процесс возникновения магнитного поля под действием изменяющегося во времени электрического поля также логически следует из принципа относительности и полевой теории близкодействия. Неподвижный электрический заряд создает электростатическое поле, если же перейти в систему отсчета, в которой этот заряд движется равномерно, то в этой системе отсчета будет существовать и магнитное поле. Появление это поля качественно можно истолковать следующим образом: пусть в некоторой точке A в некоторый момент времени движущийся со скоростью \(~\vec \upsilon\) заряд q создает электрическое поле напряженности \(~\vec E_0\) (Рис. 125). При смещении заряда напряженность электрического поля будет изменяться по величине и по направлению. Изменяющееся в рассматриваемой точке электрическое поле и создает в этой точке магнитное поле.
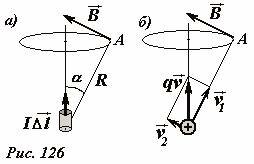
Попытаемся связать между собой характеристики электрического и магнитного полей. Для этого воспользуемся законом Био-Савара. Элемент тока \(~I \Delta \vec l\) в произвольной точке A создает магнитное поле, индукции которого равна
где R - расстояние от элемента тока до точки A, α - угол между направлением элемента тока и направлением на точку A (Рис. 126а). Направлен вектор индукции перпендикулярно элементу тока и отрезку, соединяющему его с точкой A. Характеристику элемента тока \(~I \Delta \vec l\) можно представить в виде
где q - величина заряда, движущегося внутри выделенного элемента тока. Следовательно, можно утверждать, что заряд q, движущийся со скоростью \(~\vec \upsilon\), создает магнитное поле величиной
Движущийся заряд создает также и электрическое поле, в отличие от элемента тока, в котором заряды одного знака движутся, а равные по величине заряды противоположного знака покоятся. Проведенная нами замена элемента тока на движущийся заряд законна, так как магнитное поле создается только движущимися зарядами.
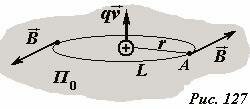
Разложим вектор скорости \(~\vec \upsilon\) заряженного тела на две составляющие (Рис. 126б)\[~\vec \upsilon_1\] - направленную вдоль отрезка, соединяющей заряд с точкой наблюдения, и \(~\vec \upsilon_2\) - перпендикулярную этому отрезку. Как следует из закона Био-Савара, вижущийся заряд не создает магнитного поля в точках, лежащих на прямой вдоль вектора скорости. Поэтому, можно сказать, что магнитное поле в точке A создается благодаря перпендикулярной компоненте скорости \(~\vec \upsilon_2\) . Это обстоятельство отражено и в формуле (3), где фигурирует произведение υ sin α, равное модулю перпендикулярной компоненты скорости υ2. Таким образом, можно упростить рассматриваемую задачу, рассматривая поля в точках плоскости П0, проходящей через заряд и перпендикулярной вектору заряда (Рис. 127).
По аналогии с законом электромагнитной индукции можно предположить, что циркуляция вектора индукции связана с изменением потока вектора напряженности электрического поля, поэтому найдем эти величины и попытаемся найти связь между ними. Рассмотрим наиболее простой случай. На окружности L, центр которой совпадает с зарядом, вектор индукции направлен по касательной к этой окружности и постоянен по модулю. Поэтому циркуляция вектора индукции по этому контуру равна
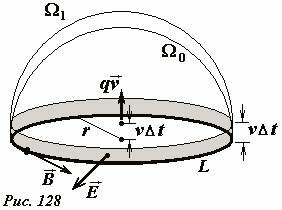
Найдем изменение потока вектора напряженности электрического поля через рассматриваемый контур L. Как и в случае расчета магнитного «потока через контур», мы должны выбрать поверхность, опирающуюся на контур. Пусть в рассматриваемый момент времени заряд находится в плоскости П0. В качестве поверхности, через которую рассчитывается поток, выберем полусферу Ω0, опирающуюся на окружность L (Рис. 128). Через малый промежуток времени Δt заряд сместится на расстояние υΔt. Чтобы найти электрический поток в этот момент времени дополним сместившуюся полусферу Ω1 тонким цилиндрическим слоем, соединяющим край полусферы с окружностью L (на рис. 125 этой слой затенен). Понятно, что изменение потока через контур равно потоку через выделенную полоску. Так как полоска узкая, то можно считать, что во всех ее точках вектор напряженности электрического поля направлен по нормали к поверхности и постоянен по модулю, поэтому искомый поток равен
где \(~E = \frac{q}{4 \pi \varepsilon_0 R^2}\) - напряженность электрического поля точечного заряда, \(S = 2 \pi R \cdot \upsilon \Delta t\) - площадь выделенной полоски. Сравнивая это выражение с формулой для циркуляции вектора магнитной индукции (6), мы видим, что наша гипотеза оправдалась: действительно, циркуляция вектора индукции пропорциональна изменению потока вектора напряженности электрического поля
Тем самым мы пришли к той же формулировке закона, описывающего токи смещения.
В данном выводе сделано одно неявное допущение: мы приняли, что напряженность электрического поля движущегося заряда определяется, так же как и напряженность поля неподвижного заряда. Строго говоря, это условие выполняется только при скоростях движения зарядов значительно меньших скорости света. Однако, полученный закон, связывающий характеристики изменяющегося электрического поля и создаваемого им магнитного поля справедлив при любых скоростях движущихся зарядов.
Примечания
- ↑ Если возникновение электрического поля под действием переменного магнитного поля называется электромагнитная индукция, то обратный процесс разумно бы назвать магнитоэлектрическая индукция, однако такой термин не используется.
- ↑ Отсутствие нормальной к контуру составляющей обосновывается теоремой о магнитном потоке. Эти рассуждения мы использовали при рассмотрении магнитного поля прямого тока.
- ↑ При описании электрического поля в диэлектриках вводят вспомогательную величину, частично обусловленную поляризацией диэлектрика, которая называется электрическим смещение, в вакууме она равна \(~\varepsilon_0 \vec E\)