Слободянюк А.И. Физика 10/16.7
§16. Превращение энергии в электрических и магнитных явлениях
16.7 Изменение энергии конденсатора при изменении его емкости.
Энергия конденсатора зависит от его емкости. Емкость конденсатора можно изменять, когда он заряжен - при этом будет изменяться его энергия. При рассмотрении этих процессов можно выделить два принципиально различных случая: первый - изменение емкости происходит при неизменных зарядах на обкладках; второй – емкость конденсатора изменяется при постоянном напряжении между обкладками (в этом случае конденсатор подключен к источнику постоянной ЭДС).
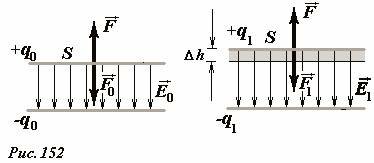
Рассмотрим теперь превращения энергии при изменении емкости плоского конденсатора, образованного двумя параллельными одинаковыми платинами площади S. Размеры пластин будем считать значительно превышающими расстояние между ними, что позволяет пренебречь краевыми эффектами, то есть считать электрическое поле \(~\vec E\) однородным (Рис. 152). Пусть конденсатор заряжен, так что заряды каждой пластины одинаковы по модулю и равны q и противоположны по знаку, поверхностная плотность заряда на каждой пластине равна \(~\sigma = \frac{q}{S}\). Напряженность поля между пластинами в этом случае равна
причем заряды каждой пластины создают поле, напряженность которого в два раза меньше напряженности суммарного поля (1); разность потенциалов между пластинами равна
Так заряды пластин разноименные, то пластины будут притягиваться друг к другу с некоторой силой F. Сила, действующая на одну пластину, равна произведению ее заряда на напряженность поля, создаваемого зарядом второй пластины,
Этой формуле можно придать иной вид, если выразить силу через напряженность электрического поля с помощью формулы (1)
Важно отметить, что давление электрического поля на проводящую платину в точности равно объемной плотности энергии поля
Чтобы изменить (для определенности увеличить см. Рис. 152) расстояние между пластинами, к ним необходимо приложить внешнюю силу F0, превышающую по модулю силе электрического притяжения. При перемещении пластины (увеличении расстояния) на величину Δh эта внешняя сила совершит положительную работу.
Если пластины конденсатора изолированы, то электрический заряд и, как следствие, напряженность поля и сила притяжения не зависят от расстояния между пластинами. Поэтому работа внешней силы по перемещению пластины на расстояние Δh будет минимальна, когда эта сила равна силе притяжения между пластинами, при этом
Благодаря этой работе возрастает энергия электрического поля – при неизменной напряженности и плотности энергии возрастает объем, занятый полем (\(\Delta V = S \Delta h\)), что выражается формулой
При увеличении расстояния между пластинами емкость конденсатора изменяется (уменьшается). Изменение энергии конденсатора можно также рассчитать, с помощью формулы для его энергии, причем следует выразить энергию через не изменяющийся в данном случае заряд конденсатора, то есть
Эта формула равносильна полученным выше выражениям для изменения энергии. Таким образом, в рассмотренном процессе превращения энергии понятны: работа внешней силы увеличивает энергию электрического поля конденсатора.
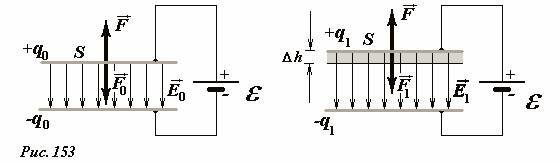
Рассмотрим теперь этот же процесс при условии, что обкладки конденсатора подключены к источнику постоянной ЭДС (Рис. 153). В этом случае при изменении расстояния между пластинами, остается неизменным напряжение U = ε между ними.
В этом случае разноименно заряженные пластины также притягиваются, поэтому для увеличения расстояния между ними внешняя сила также совершает положительную работу, однако при этом энергия конденсатора уменьшается, а не растет! Действительно, при постоянном напряжении между пластинами, изменение энергии конденсатора рассчитывается по формуле
Так как h1 > h0 , то C1 < C0 и ΔWC < 0.
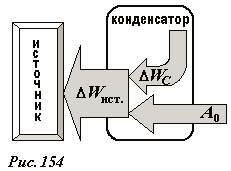
Но и в этом случае нарушения закона сохранения энергии нет, переданная системе энергия (равная совершенной работе) не «теряется» - конденсатор не является замкнутой системой, он же подключен к источнику ЭДС. При увеличении расстояния между пластинами емкость конденсатора уменьшается, поэтому уменьшается заряд на пластинах, которому некуда деться, кроме как вернуться назад, в источник. Их возращению препятствуют сторонние силы (вспомните – сторонние силы источника стремятся «вытолкнуть заряды из источника), поэтому при возвращении зарядов энергия источника повышается. Таким образом, при раздвигании пластин конденсатора происходит подзарядка источника, а энергия, переданная посредством совершенной работы, переходит в энергию источника. Кроме того, энергия поля в конденсаторе также уменьшается, поэтому эта «потеря» энергии также переходит в источник. Иными словами, при перемещении пластины внешняя сила не только совершает работу по подзарядке источника, но и «заставляет» электрическое поле вернуть часть своей энергии. Схематически потоки энергии в этом процессе показаны на Рис. 154.
Подтвердим проведенные рассуждения расчетами энергетического баланса и покажем, что он точно выполняется. Силу притяжения между пластинами (4) выразим через постоянное напряжение между пластинами
В данном случае эта сила зависит от расстояния между пластинами. Поэтому для расчета работы необходимо разбить процесс движения пластины на малые участки и затем просуммировать работы на этих участках. Чтобы избежать этой громоздкой математической процедуры, будем считать, что смещение Δh мало настолько, что можно пренебречь изменением силы притяжения. В этом приближении работа внешней силы будет равна
Преобразуем также выражение для изменения энергии конденсатора с учетом малости смещения. Запишем \(h_1 = h_0 + \Delta h\) и подставим в формулу (9)
Наконец, найдем работу по зарядке источника, которая равна произведению «вернувшегося» заряда на ЭДС источника (которая равна напряжению конденсатора):
Итак, проведенный расчет полностью подтверждает сделанные ранее заключения: увеличение энергии источника (что равносильно - работа по его подзарядке) равно сумме работы внешней силы и уменьшения энергии поля конденсатора
Задание для самостоятельной работы.
- Докажите, что в рассмотренном процессе энергетический баланс выполняется при любом (не малом) смещении пластины.
Признавая, что «аналогии ничего не доказывают, но много объясняют», рассмотрим гидростатическую аналогию преобразования энергии при изменении «емкости» сосуда. Как мы указывали, аналогом электрического заряда может служить объем жидкости, налитой в сосуд, аналогом изменения потенциала – изменение уровня жидкости, тогда аналогом электроемкости вертикального сосуда служит площадь его дна. Таким образом, изменению емкости должно соответствовать изменение площади поперечного сечения сосуда. Представим себе сосуд в форме параллелепипеда (аквариума), одна из стенок которого может двигаться – при ее смещении изменяется площадь сосуда, то есть изменяется его «емкость». При уменьшении площади сосуда уменьшается «емкость». В рассмотренных электростатических примерах – уменьшению емкости конденсатора соответствует увеличению расстояния между его пластинами.
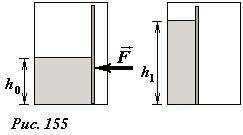
Пусть теперь в нашем сосуде находится некоторый объем жидкости, уровень которой равен h0 (Рис. 155 ). Чтобы сместить подвижную стенку, к ней необходимо приложить некоторую внешнюю силу F. Если объем жидкости в сосуде сохраняется, то при смещении стенки ее уровень повышается, следовательно, увеличивается ее энергия. Понятно, что увеличение потенциальной энергии жидкости равно работе внешней силы.
Сравните: при неизменном объеме жидкости (электрическом заряде) уменьшение площади сосуда (емкости конденсатора) под действием внешней силы приводит к возрастанию уровня жидкости (разности потенциалов) и гидростатической энергии жидкости (электростатической энергии поля).
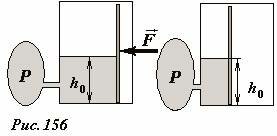
Если конденсатор подключен к источнику постоянной ЭДС, то его напряжение поддерживается постоянным. В гидростатической аналогии необходимо в этом случае говорить о постоянной высоте уровня жидкости в сосуде. В качестве устройства, поддерживающего постоянный уровень можно предложить, например, резиновый сосуд («грушу»), жидкость в которой поддерживается при постоянном давлении. Если теперь наш сосуд «переменной емкости» подключить к источнику постоянного давления (резиновой груше), то получим аналог конденсатора, подключенного к источнику постоянной ЭДС (Рис.156) При смещении подвижной стенки в этом случае внешняя сила также совершает положительную работу, но потенциальная энергия жидкости в сосуде уменьшается, так как уменьшается ее объем при неизменной высоте уровня. Под действием этой внешней силы часть жидкости из сосуда заталкивается в резиновую грушу, при этом энергия последней возрастает. Увеличение ее энергии равно сумме работы внешней силы и уменьшения потенциальной энергии жидкости в сосуде.
Сравниваем: при постоянном уровне жидкости в сосуде (напряжении конденсатора) уменьшение площади дна (емкости конденсатора) под действием внешней силы приводит к возвращению части жидкости (электрического заряда) в резиновый сосуд, поддерживаемый при постоянном давлении (источник постоянной ЭДС). При этом увеличение энергии жидкости в резиновом сосуде постоянного давления (источника ЭДС) равно сумме работы внешней силы и уменьшения потенциальной энергии жидкости в сосуде (энергии конденсатора).
Задание для самостоятельной работы.
- Докажите, что в рассмотренных гидростатических аналогиях энергетический баланс выполняется точно.
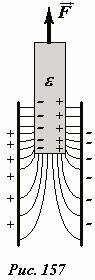
Электроемкость конденсатора зависит также от диэлектрической проницаемости вещества, находящегося между обкладками. Поэтому емкость конденсатора можно изменять, меняя вещество, находящееся между обкладками. Пусть, например, между обкладками плоского конденсатора находится диэлектрическая пластинка. Если конденсатор заряжен, то для извлечения пластинки необходимо приложить к ней внешнюю силу и совершить положительную работу. Механизм возникновения силы, действующей на пластинку со стороны электрического поля, проиллюстрирован на Рис. 157. При ее смещении изначально однородное распределение зарядов на обкладках конденсатора и поляризационных зарядов на пластинке искажается. Как следствие этого перераспределения зарядов искажается и электрическое поле, поэтому возникаю силы, стремящиеся втянуть пластинку внутрь конденсатора.
Расчет этих сил сложен, но энергетические характеристики происходящих процессов могут быть найдены без особого труда. С формальной точки зрения, не важно чем вызваны изменения емкости конденсатора, поэтому можно воспользоваться всеми рассуждениями и выводами предыдущего раздела, как для случая изолированного конденсатора (при сохранении заряда), так для конденсатора подключенного к источнику постоянной ЭДС.
Чрезвычайно интересными и практически важными являются энергетические характеристики процессов поляризации диэлектриков, однако их расчет представляет собой весьма сложную задачу. Для решения возникающих здесь проблем требует привлечения сведения о строении вещества. Некоторые из этих вопросов мы рассмотрим в следующем году после ознакомления с основами теории строения вещества.