Слободянюк А.И. Физика 10/18.6

Содержание книги

Предыдующая страница

§18. Переменный электрический ток

18.6 Цепи переменного тока. Резонанс напряжений.

Полученные соотношения между амплитудами токов и напряжений, а также определяющие сдвиг фаз между ними, позволяют рассчитать характеристики любой цепи переменного тока. Принципиально методика расчета характеристик цепей переменного тока не отличается от методики расчета цепей постоянного тока – физические законы, выраженные в правилах Кирхгофа, справедливы для мгновенных значений токов и напряжений на любом участке цепи. Однако в случае переменных токов ситуация осложняется чисто математическими проблемами – как от уравнений для мгновенных значений токов и напряжений перейти к их амплитудным (или действующим) величинам, к разностям фаз, определяющим, энергетические характеристики рассматриваемых цепей? Именно для преодоления этих математических трудностей разработаны различные математические методы расчета, одним из которых является метод векторных диаграмм.

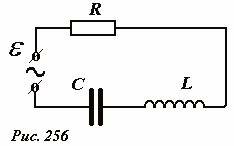
Применим этот метод для описания цепи, изображенной на рис.256: к источнику переменной ЭДС последовательно подключены резистор, катушка индуктивности и конденсатор. Для расчета характеристик цепи запишем уравнение закона Ома для полной цепи (суммарная ЭДС контура равна сумме напряжений на элементах этого контура)

\(~\varepsilon + \varepsilon_{si} = U_R + U_C\) . (1)

здесь \(U_R = IR\), напряжение на резисторе, \(~U_C = \frac{q}{C}\) - напряжение на конденсаторе, \(\varepsilon_{si} = - LI'\) - ЭДС самоиндукции, возникающая в катушке индуктивности. Зависимость ЭДС источника от времени представим в традиционной форме (внутренним сопротивлением источника пренебрегаем)

\(~\varepsilon = U_0 \cos \omega t\) . (2)

Уравнение, конечно, (1) может быть решено аналитически: для этого необходимо представить зависимость силы тока от времени в общей тригонометрической форме \(I = I_0 \cos (\omega t + \varphi)\), и подставить его в уравнение (при этом напряжение на конденсаторе и ЭДС самоиндукции должны быть выражены через параметры силы тока), после чего провести разложения тригонометрических функций, приравнять коэффициенты при синусах и косинусах, решить полученную систему алгебраических уравнений. Такой путь очень длинный, поэтому мы пойдем другим…

Перепишем уравнение (1) в форме, справедливой для мгновенных значений

\(~\varepsilon(t) = U_R(t) + U_C(t) + U_L(t)\) , (3)

где \(U_L = LI'\) , напряжение на катушке, необходимое для преодоления противодействующей ЭДС самоиндукции. Теперь можно поступать формально, как при расчете цепей постоянного тока. Так как все элементы цепи соединены последовательно, то сила тока одинакова во всех точках цепи, сумма напряжений на всех элементах цепи равна ЭДС источника. Для цепей постоянного тока на основании этих законов, мы получали уравнение для определения силы тока в цепи. Для рассматриваемой цепи переменного тока подход к расчету аналогичен, только ситуация осложняется наличием различных сдвигов фаз между током и напряжением на элементах цепи. Только для преодоления этой сложности нам приходится строить векторные диаграммы токов и напряжений.

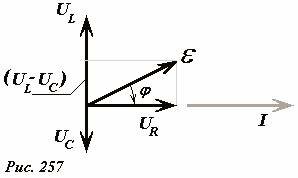
Для рассматриваемой цепи это построение проводится в следующем порядке (Рис.257): выбираем произвольное направление (на рисунке – горизонтальное), вдоль которого направляем вектор I, изображающий колебания силы тока. Модуль этого вектора и его направление относительно вектора ЭДС источника подлежат определению. Можно сказать, что мы «рисуем уравнение» относительно неизвестного вектора силы тока. Далее в соответствии с рисунками 247, 249, 253 строим векторы напряжений на резисторе, конденсаторе и катушке индуктивности, затем строим вектор суммы векторов напряжений, которая в соответствии с уравнением (3) равна ЭДС источника. Наконец, используя теорему Пифагора, записываем соотношение для амплитудных значений напряжений и ЭДС

\(~U^2_0 = U^2_{R0} + (U_{L0} - U_{C0})^2\) . (4)

Обратите внимание, на сколько соотношение для амплитудных значений отличается от соотношения (3) для соответствующих мгновенных значений.

Наконец, выражаем амплитудные значения напряжений через амплитудное значение силы тока \(U_{R0} = I_0 R\), \(U_{C0} = \frac{1}{\omega C} I_0\) , \(U_{L0} = \omega L I_0\) и подставляем их в выражение (4), в результате чего получаем уравнение для определения амплитуды силы тока

\(~U^2_0 = I^2_0 R^2 + \left(\omega L I_0 - \frac{1}{\omega C} I_0 \right)^2\) . (5)

Решение этого уравнения элементарно

\(~I_0 = \frac{U_0}{\sqrt{R^2 + \left(\omega L - \frac{1}{\omega C} \right)^2}}\) . (6)

Также из векторной диаграммы легко определяется сдвиг фаз между ЭДС источника и силой тока в цепи, эта величина подчиняется соотношению

\(~\operatorname{tg} = - \frac{U_{L0} - U_{C0}}{U_{R0}} = - \frac{\omega L - \frac{1}{\omega C}}{R}\) . (7)

Формулы (6)-(7) дают полное решение поставленной задачи, определяют зависимость силы тока в цепи от времени.

Задание для самостоятельной работы.

1. Покажите, что в данной цепи работа источника равна количеству теплоты, выделяющейся на резисторе (активном сопротивлении).

Проанализируем выражение (6) для амплитуды силы тока. Полученная функция I₀(ω) показывает, что сила тока сложным образом зависит от частоты источника. Из виды этой функции следует, что она имеет максимум, если второе слагаемое под корнем обращается в нуль

\(~\omega L - \frac{1}{\omega C} = 0\) ,

то есть, когда частота источника становится равной

\(~\omega_0 = \frac{1}{\sqrt{LC}}\) . (8)

В этом случае амплитуда силы тока принимает максимальное значение равное

\(~I_{max} = \frac{U_0}{R}\) , (9)

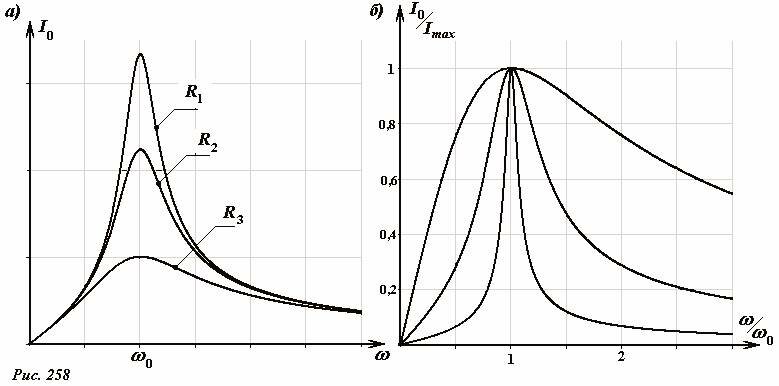
которое не зависит от емкости конденсатора и индуктивности катушки. При частоте стремящейся к нулю и частоте стремящейся к бесконечности сила тока стремится к нулю. Схематические графики зависимостей амплитуды силы тока от частоты показаны на рис. 258. Разные кривые соответствуют разным значениям активного сопротивления, причем R₁ < R₂ < R₃.

Интересно качественно объяснить такое поведение рассматриваемых зависимостей. Так при малых частотах источника, бесконечно возрастает сопротивление конденсатора (постоянный ток через конденсатор не протекает!), а при больших частотах резко возрастает сопротивление катушки индуктивности (из-за резкого возрастания ЭДС самоиндукции). Если же частота источника совпадает с частотой ω₀, то сила тока в цепи полностью определяется ее активным сопротивлением. Взгляните на векторную диаграмму – при этой частоте амплитуды напряжений на конденсаторе и катушке равны, а так как они изменяются в противофазе, то в любой момент полностью компенсируют друг друга. Иными словами, при этой частоте эти элементы как бы «выпадают» из цепи. Механизм этого эффекта заключается в том, что в моменты зарядки конденсатора максимальна ЭДС самоиндукции, и, наоборот, когда ЭДС самоиндукции максимально препятствует ЭДС источника, разряжается конденсатор, поддерживая ток в цепи. В этом режиме осуществляется перекачка энергии между конденсатором и катушкой – энергия электрического поля конденсатора переходит в энергию магнитного поля катушки и обратно, причем эта «перекачка» не влияет на работу источника. Рассмотренное явление резкого возрастания амплитуды силы тока в цепи с последовательно соединенными конденсатором и катушкой индуктивности получило название резонанса напряжений, а частота, определяемая формулой (8) называется резонансной.

Рассмотренная зависимость амплитуды силы тока от частоты является много параметрической (так как зависит от ЭДС источника, активного сопротивления, емкости и индуктивности цепи). Имеет смысл перейти к некоторым безразмерным переменным, чтобы унифицировать построенные зависимости. Наиболее естественно, в качестве аргумента этой функции выбрать относительную частоту – отношение частоты источника к резонансной частоте цепи

\(~\xi = \frac{\omega}{\omega_0}\) . (10)

Тогда подставляя выражение для частоты \(~\omega = \omega_0 \xi = \frac{\xi}{\sqrt{LC}}\) в функцию (6), получим

\(~I_0(\xi) = \frac{U_0}{\sqrt{R^2 + \left(\frac{\xi}{\sqrt{LC}} L - \frac{\sqrt{LC}}{\xi C} \right)^2}} = \frac{U_0}{\sqrt{R^2 + \frac{L}{C} \left(\xi - \frac{1}{\xi} \right)^2}} = \frac{U_0}{R} \frac{1}{\sqrt{1 + \frac{L}{CR^2} \left(\xi - \frac{1}{\xi} \right)^2}}\) .

Далее удобно ввести в качестве функции отношение амплитуды силы тока к ее максимальному значению \(\eta = \frac{I_0}{I_{max}}\), и обозначить единственный безразмерные параметр цепи \(~\beta = \frac{L}{CR^2}\). Тогда изучаемая зависимость становится однопараметрической и приобретает вид

\(~\eta(\xi) = \frac{1}{\sqrt{1 + \beta \left(\xi - \frac{1}{\xi} \right)^2}}\) . (11)

Графики этих функций показаны на рис. 258 б. Безразмерный параметр цепи влияет только на ширину максимума, чем больше этот параметр (чем меньше активное сопротивление), тем резонансная кривая уже и резче.

Примечания

Следующая страница