Слободянюк А.И. Физика 10/2.6
§2. Кинематическое описание механического движения материальной точки
2.6 Равномерное движение материальной точки вдоль прямой
Напомним, что равномерным называется движение с постоянной скоростью. Так как скорость величина векторная, то постоянство скорости предполагает постоянство и направления движения, то есть движение по прямой линии [1]. При таком движении можно совместить направление одной из осей системы координат вдоль траектории движения, тогда движение материальной точки полностью описывается одной функцией.
Найдем зависимость координаты от времени (закон движения) при равномерном движении вдоль прямой. Непосредственно из формулы \(~\upsilon = \frac{\Delta x}{\Delta t}\) , определяющей скорость движения, можно выразить
Эта формула дает закон движения материальной точки при ее равномерном движении вдоль прямой. Знание только скорости движения не позволяет однозначно определить его закон - необходимо знать положение (то есть координату) тела в какой-то момент времени. Часто это дополнительное условие называют начальным - в начальный момент времени t0 тело находится в точке с координатой x0 . Однако, совсем не обязательно, чтобы движение начиналось в момент времени t0 - формулу (1) можно применять для любых времен t (в том числе и t < t0 ), важно только, чтобы во все рассматриваемые моменты времени продолжалось движение с той же скоростью. В этом смысле закон движения обратим - его можно использовать как для того, чтобы предсказать положение тела в будущем (t > t0), так и для того, чтобы определить, где оно находилось в прошлом (t < t0).
При рассмотрении системы координат мы неоднократно подчеркивали, что выбор начала отсчета координат произволен, так же произволен и выбор начала отсчета времени t0. Физический смысл этого «произвола» - вы можете пустить свои часы в любой удобный для вас момент времени. Поэтому часто в формуле закона движения полагают, что t0 = 0, тогда
Различие между формулами (1) и (2) при описании одного и того же движении только в начальном отсчете времени: при описании движения с помощью формулы (1) полагают, что тело находилось в точке с координатой x0 при t = t0 , а в формуле (2) при t = 0.
С математической точки зрения закон движения является функцией, и как всякая функция может быть проиллюстрирован графиком. Графическое представление различных законов наглядно, информативно и чрезвычайно распространено как в физике, так и в других естественных науках.
Построим график функции, описываемой уравнением (1). Зависимость x(t) в данном случае линейна, поэтому ее график является прямой линией (рис. 12). Эта прямая проходит через точку [2] A с координатами (t0,x0). Точки пересечения графика с осями координат также имеют наглядный физический смысл: x1 - положение тела в момент времени t = 0 ; t2 - момент времени, когда тело находилось в точке начала отсчета. Наклон графика определяется скоростью точки - чем выше скорость, тем больший угол образует график с осью t.
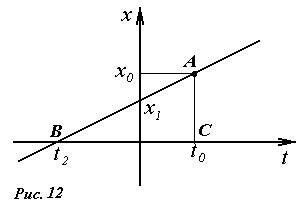
Иногда говорят, что скорость численно равна тангенсу угла наклона графика закона движения к оси времени. Действительно, в прямоугольном треугольнике АВС длина отрезка ВС равна Δt, а длина отрезка АС равна Δx. Следовательно, их отношение, с одной стороны равно скорости движения \(~\upsilon = \frac{\Delta x}{\Delta t}\) , а, с другой - тангенсу угла ∠ ABC. К этому утверждению следует относиться с большой осторожностью, так как изменения координаты Δx и времени Δt являются физическими величинами и имеют разные размерности, поэтому масштабы соответствующих осей могут выбираться произвольно, независимо друг от друга. Изменение масштаба одной из осей приведет к изменению угла наклона графика, скорость же при этом, конечно, не изменится. Поэтому измерять скорость с помощью транспортира не разумно. Поэтому «тангенс наклона» \(~\frac{\Delta x}{\Delta t}\) следует понимать как отношение физических величин, а не длин отрезков на рисунке с произвольным масштабом. Во избежание подобной путаницы в дальнейшем для обозначения отношения \(~\frac{\Delta x}{\Delta t}\) мы будем использовать термин - коэффициент наклона.
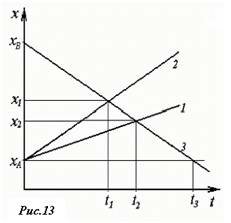
На рис. 13 приведены графики законов движения нескольких человек вдоль одной прямой, причем их движение может быть словесно описано следующим образом: «Из пункта A (расположенного в точке с координатой xA) одновременно вышли два пешехода, причем второй двигался со скоростью в два раза большей скорости первого. Навстречу им из пункта B (расположенного в точке с координатой xB) вышел третий пешеход, со скоростью равной скорости второго. Третий пешеход встретил второго в момент времени t1 в точке с координатой x1, а затем первого в момент времени t2 в точке с координатой x2. В момент времени t3 он прибыл пункт A.» Вот такая «история» изображена на этом графике! Согласитесь, графический способ описания гораздо короче и нагляднее.
В том случае, когда мы описываем движение нескольких тел в разных направлениях, неразумно для каждого тела вводить свою систему координат. В такой ситуации предпочтительнее ввести одну систему координат, а движение каждого тела описывать в векторной форме.
Непосредственно из определения вектора скорости \(~\vec \upsilon = \frac{\Delta \vec r}{\Delta t}\) следует, что векторная запись закона равномерного движения имеет вид
где \(~\vec r\) - радиус-вектор точки в произвольный момент времени t, \(~\vec r_0\) - радиус-вектор точки в некоторый момент времени t0. По поводу закона движения (3) можно повторить все рассуждения, касающиеся необходимости задания начальных условий, приведенные ранее.
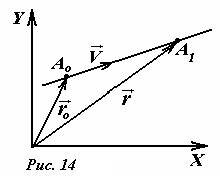
Заметим, что уравнение (3), как любое векторное соотношение, имеет наглядную геометрическую интерпретацию (рис.14), причем величина \(~\vec \upsilon (t - t_0)\) также является вектором и может быть изображена в виде направленного отрезка A0A1 .
Мы построили и описали одну из моделей механического движения, которая как всякая модель упрощает действительное движение. Но эта модель может применяться (и применяется!) для описания некоторых реальных движений. Необходимо только строго очертить рамки ее применимости, которые определяются постановкой задачи - насколько подробно, детально и с какой точностью требуется описать движение. По определению, движение является равномерным, если за равные промежутки времени тело проходит равные отрезки пути. Следовательно, движение можно считать (моделировать) равномерным, если можно пренебречь различиями в расстояниях, проходимых телом за равные промежутки времени.
Примечания
- ↑ Тем не менее, достаточно часто говоря о равномерном движении, подразумевают постоянство только модуля, величины скорости. В этом смысле правомочно говорить, например, о равномерном движении по окружности.
- ↑ У нас начинают проявляться недостатки разговорного языка: «материальная точка (модель тела) находится в точке (положение тела в пространстве) с координатой x0, что соответствует точке А (точка на рисунке) на графике закона движения». Эти недостатки создают определенные трудности, однако в большинстве случаев из смысла фразы понятно о каких «точках» и «координатах» идет речь.
Смотреть HD
видео онлайн
бесплатно 2022 года
