Слободянюк А.И. Физика 10/6.6
§6. Законы сохранения в механике
6.6 Потенциальная энергия деформированной пружины.
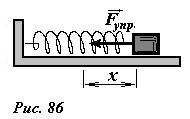
Деформированная (например, растянутая) пружина способна совершить работу. Действительно, если к растянутой пружине прикрепить некоторое тело, то пружина будет действовать на него с некоторой силой, под действием которой тело начнет смещаться, следовательно, будет совершена работа (рис. 86).
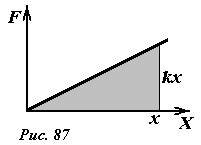
Сила, с которой пружина действует на тело, не является постоянной, поэтому для вычисления работы воспользуемся графическим методом. Построим график зависимости силы упругости F = kx от координаты, который является прямой линией (рис. 87). Площадь выделенного треугольника под графиком равна максимальной работе, которую может совершить пружина, понятно, что она равна
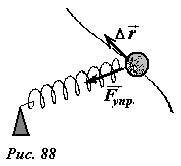
Для того чтобы пружине приписать потенциальную энергию, равную максимальной работе (1) необходимо показать, что эта работа не зависит от траектории движения тела. Чтобы доказать это утверждение, достаточно рассмотреть работу на малом участке перемещения \(~\Delta \vec r\) при движении по произвольной траектории (рис. 88). В данном случае эта работа \(~\delta A = \vec F \cdot \Delta \vec r = kx \cdot \Delta r \cos \alpha = kx \cdot \Delta x\) , полностью определяется изменением деформации пружины x, поэтому она не зависит от траектории движения тела.
Таким образом, силы упругости, подчиняющиеся закону Гука, являются потенциальными, и потенциальная энергия деформированной пружины определяется формулой
Нулевой уровень потенциальной энергии, рассчитываемой по формуле (2), соответствует недеформированной пружине.
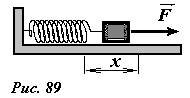
Подсчитаем, какую минимальную работу следует совершить, чтобы пружину, жесткостью k, растянуть на величину x (рис. 89). Чтобы деформировать пружину, к ней необходимо приложить внешнюю силу. Очевидно, что эта работа будет минимальная в том случае, когда внешняя приложенная сила в любой точке равна силе упругости, действующей со стороны пружины, поэтому работа этой силы будет равна \(~A = \frac{kx^2}{2}\) , то есть увеличению потенциальной энергии пружины.