Слободянюк А.И. Физика 10/7.1
§7. Механика жидкости и газа
Рассмотренные нами методы описания механического движения, законы, управляющие этим движением, в принципе, позволяют изучать движение любой механической системы. Основные проблемы, возникающие при этом, носят скорее математический характер – может понадобиться слишком много переменных, слишком много уравнений, слишком много расчетов. Поэтому до настоящего времени продолжаются научные исследования в области механики – строятся новые модели, разрабатываются новые (в том числе компьютерные) методы решения уравнений, анализируются возможности применения различных упрощений и приближений.
В данном параграфе мы рассмотрим основы описания движения жидкостей и газов. Данный раздел физики называется гидродинамика и аэродинамика. Даже основные уравнения этого раздела чрезвычайно сложны, их формулировка и обоснование требует привлечения не только законов механики, но и законов, описывающих процессы теплопередачи, упругих свойств жидких и газообразных сред, и других. Поэтому мы только наметим некоторые основные идеи, тем более что математический аппарат, привлекаемый для описания вполне наглядного движения жидкости, понадобится нам при изучении более абстрактных электрических и магнитных полей.
7.1 Модель сплошной среды, «точечные» характеристики вещества.
Хорошо известно, что все тела, в том числе жидкие газообразные, состоят из молекул. Поэтому если задать положение каждой молекулы в произвольный момент времени, то движение жидкости или газа будет описано очень подробно. Однако очевидно, что выполнение этой программы невозможно [1] – достаточно вспомнить, что в 1 см3 содержится более чем 1019 молекул. Чтобы только выписать нужное число уравнений движения не хватит ни бумаги, ни чернил, ни времени. Более того, такое сверхподробное описание является явно излишним, извлечь полезные сведения из такого массива информации просто невозможно. Итак, нам необходим принципиально иной способ описания движения жидкости.
Прежде всего, отметим, что в подавляющем большинстве случаев описания движения жидкостей и газов нет необходимости рассматривать молекулярную структуру – так как размеры движущихся объемов жидкости, размеры движущихся в жидкости твердых тел значительно превышают размеры молекул. Поэтому в этих случаях используется модель сплошной среды. В рамках этой модели газ или жидкость рассматривается как среда, все характеристики которой плавно и непрерывно изменяются от одной геометрической точки к другой. В рамках такой модели можно вводить «точечные» характеристики среды (например, плотность, удельная теплоемкость, вязкость, показатель преломления, удельное электрическое сопротивление) и рассматривать их как функции координат точек среды. Если свойства среды одинаковы во всех точках пространства, то такая среда называется однородной. С точки зрения математики использование модели сплошной среды означает переход от дискретного к непрерывному описанию. Рассмотрим для примера понятие плотности неоднородной среды. Для однородного вещества плотность ρ равна отношению массы тела m к его объему V, или массе единицы объема тела - \(~\rho = \frac{m}{V}\) . Для однородного вещества отношение массы к объему является величиной постоянной.
В качестве примеров неоднородных веществ можно привести смеси различных веществ; земную атмосферу, плотность которой уменьшается с высотой, плохо перемешенные растворы и т.д.
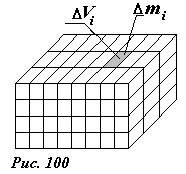
Для тела, изготовленного из неоднородного вещества, введенное понятие плотности \(~\rho = \frac{m}{V}\) дает только среднее значение плотности тела. Для более подробного описания распределения масс в таких телах, можно мысленно разбить тело на малые части (рис. 100), указать номер i «кусочка», определить его объем Vi и массу mi, рассчитать среднюю плотность \(~\overline {\rho_i} = \frac{m_i}{V_i}\) . Для увеличения точности описания число частей должно увеличиваться, соответственно будет возрастать и число средних плотностей. Фактически набор величин ρi представляет собой среднюю плотность как функцию номера выделенной части. Понятно, что такое описание не очень удобно.
Поэтому принят другой метод описания распределения масс внутри неоднородного тела. Выберем внутри тела точку с координатами (x,y,z) и вокруг нее очертим некоторый объем ΔV (его форма – кубик, шарик … несущественна), определим массу вещества, содержащегося внутри выделенного объема Δm и среднюю плотность этого выделенного объема \(~\overline {\rho} (x,y,z) = \frac{\Delta m}{\Delta V}\) . Далее мысленно будем уменьшать объем выделенной части, соответственно будет уменьшаться и масса этой части. Предел, к которому стремится средняя плотность при уменьшении объема, и называется плотностью вещества в данной точке
При таком определении плотность становится непрерывной функцией координат.
Аналогично определяются и другие «точечные» характеристики вещества.
С математической точки зрения для описания характеристик сплошной среды, мы используем функции нескольких переменных – координат и времени (в принципе характеристики среды могут изменяться с течением времени). Такое соответствие – когда каждой точке пространства (трем координатам) ставится в соответствие число, в математике называется скалярным полем. В этом математическом смысле говорят о поле температур, поле давлений, поле плотностей и т.д.
Обратите внимание, на формальную схожесть определения плотности «в точке» с определением мгновенной скорости. Строго говоря, понятие плотности «в точке» физического смысла не имеет – измерению поддается только средняя плотность конечного объема вещества. Особенно абсурдным становится понятие плотности газа, в пределах объема, размеры которого меньше среднего расстояния между молекулами!
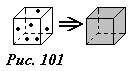
Реальный смысл имеет произведение ρ(x,y,z)ΔV равное массе вещества в малом объеме ΔV, окружающем точку с координатами (x,y,z). Тем не менее, упрощение математического описания, искупает логическую противоречивость. В некоторых случаях, говоря о бесконечно малом объеме, подразумевают физически бесконечно малый объем – с точки зрения математического описания малый, а с физической велик по сравнению со средним расстоянием между молекулами, содержащий достаточно много молекул. В таком объеме, свойства отдельных частиц (например, их массу) мы равномерно «размазываем» по всему объему, сохраняя ее суммарное значение (рис. 101).
Примечания
- ↑ Справедливости ради, отметим, что в настоящее время разрабатывается и используется, так называемый, динамический подход к исследованию молекулярных систем, в рамках которого жидкость, газ моделируется как набор небольших тел (материальных точек, жестких шариков, дисков) движущихся и взаимодействующих по законам механики. В рамках этих исследований получены достаточно интересные результаты. Однако, число частиц, входящих в моделируемую систему, мало - не превышает миллиона (106). Реализация таких моделей возможна только с помощью мощных современных компьютеров.