Слободянюк А.И. Физика 10/7.8

Содержание книги

Предыдующая страница

§7. Механика жидкости и газа

7.8 Распределение давления в идеальной жидкости, движущейся по горизонтальной трубе.

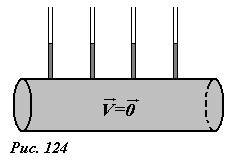
Рассмотрим распределение давления в горизонтальной цилиндрической трубе, полностью заполненной жидкостью. Для этого расположим на трубе ряд измерительных манометров, высота уровня жидкости в которых будет показывать величину давления в данном месте трубы.

Если жидкость неподвижна, то давление жидкости (и соответственно высоту жидкости в измерительных трубках) будут одинаковы во всех точках трубы (рис. 124).

Для идеальной жидкости (то есть при пренебрежении силами вязкого трения) давление внутри горизонтальной трубы остается постоянным и при равномерном движении жидкости – в этом случае нет необходимости преодолевать силы сопротивления.

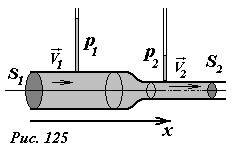
Исследуем теперь распределение давлений внутри трубы переменного сечения при движении идеальной жидкости. Пусть труба состоит из двух сочлененных частей, площади поперечных сечений которых равны S₁ и S₂ (рис. 125). В такой трубе при движении даже идеальной жидкости в области сочленения должна существовать область изменения давления. Действительно, согласно уравнению неразрывности скорости движения жидкости в разных частях трубы связаны соотношением υ₁S₁ = υ₂S₂ . Поэтому, при переходе жидкости из более широкой в более узкую части трубы скорость жидкости должна возрастать, что может произойти только благодаря действию силы, обусловленной разностью давлений в узкой и широкой частях. Причем давление в более широкой части должно быть выше.

Для упрощения расчета разности давлений представим себе, что в обеих частях трубы расположены легкие подвижные поршни. Кроме того, пренебрежем силами вязкого трения, то есть будем считать жидкость идеальной. Пусть поршень в левой части трубы сместился на расстояние h₁ , тогда поршень в правой части сместится на расстояние h₂. Из условия несжимаемости жидкости смещения поршней связаны соотношением h₁S₁ = h₂S₂ = V, где V объем жидкости прошедший через поперечное сечение трубы. На левый поршень действует внешняя сила F₁ = p₁S₁ , работа совершенная этой силой при смещении поршня будет равна A₁ = p₁S₁h₁. Правый поршень совершит работу (по перемещению жидкости за поршнем) A₂ = p₂S₂h₂ . Кроме того, при перемещении жидкости возрастает кинетическая энергия жидкости, прошедшей через место сочленения. Увеличение кинетической энергии равно \(~\Delta E_k = \frac{\rho S_2 h_2}{2} \upsilon^2_2 - \frac{\rho S_1 h_1}{2} \upsilon^2_1\) . По закону сохранения энергии работа, совершенная над левым поршнем внешней силой, равна сумме работы, совершенной правым поршнем над «внешней» жидкостью, и изменению кинетической энергии системы: A₁ = A₁ + ΔE_k. С учетом условия постоянства объема жидкости, это уравнение приобретает вид

\(~p_1 - p_2 = \frac{\rho \upsilon^2_2}{2} - \frac{\rho \upsilon^2_1}{2}\) . (1)

Таким образом, мы получили величину скачка давления в месте сочленения трубы, которая квадратично возрастает с ростом скорости течения.

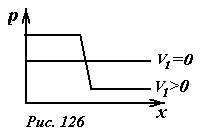
На рисунке 126 схематически показано распределение давления вдоль оси трубы, скачок давления происходит в области сочленения. При скорости движения равной нулю, давление постоянно во всех точках жидкости. Из уравнения (1) можно вычислить скорости движения и расход жидкости в зависимости от приложенной разности давлений

\(~Q = S_1 \upsilon_1 = S_2 \upsilon_2 = \sqrt{\frac{2 S^2_1 S^2_2}{S^2_1 - S^2_2} \frac{\Delta p}{\rho}}\) . (2)

Как следует из полученной формулы, расход жидкости не пропорционален приложенной разности давлений – так, для увеличения расхода жидкости в два раза, разность давлений должна быть увеличена в четыре раза.

Задания для самостоятельной работы.

1. Из формулы (1) следует, что скачок давления не зависит от направления движения жидкости. Объясните полученный результат. В какую же сторону будет двигаться жидкость, если к концам трубы приложить некоторую разность давлений?
2. Нарисуйте силы, действующие на движущуюся жидкость в трубе переменного сечения со стороны стенок трубы.
3. Из формулы (2) следует, что при выравнивании площадей поперечного сечения труб (S₂ → S₁ ) расход жидкости стремится к бесконечности. Объясните этот результат. Можно ли применять эту формулу при S₂ > S₁?

Следующая страница