Т. Капиллярные явления

Капиллярные явления

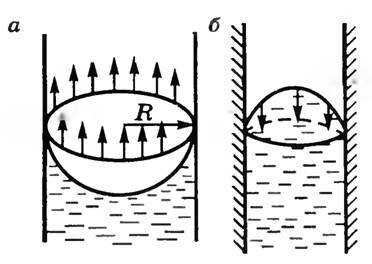
Искривление поверхности жидкости у краев сосуда особенно отчетливо видно в узких трубках, где искривляется вся свободная поверхность жидкости. В трубках с узким сечением эта поверхность представляет собой часть сферы, ее называют мениском. У смачивающей жидкости образуется вогнутый мениск (рис. 1, а), а у несмачивающей — выпуклый (рис. 1, б). Так как площадь поверхности мениска больше, чем площадь поперечного сечения трубки, то под действием молекулярных сил искривленная поверхность жидкости стремится выпрямиться.

Рис. 1

Силы поверхностного натяжения создают дополнительное (лапласово) давление под искривленной поверхностью жидкости.

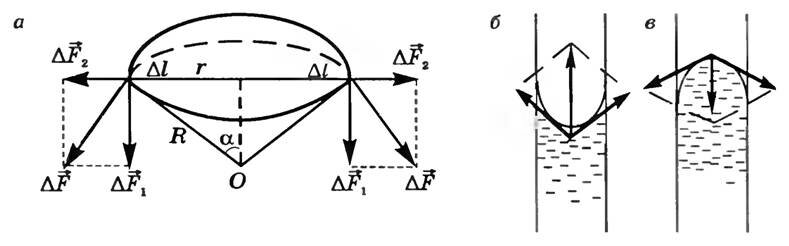
Для расчета избыточного давления предположим, что поверхность жидкости имеет форму сферы радиуса R (рис. 2. а), от которой мысленно отсечен шаровой сегмент, опирающийся на окружность радиуса r = R sin α.

Рис. 2

На каждый бесконечно малый элемент длины Δl этого контура действует касательная к поверхности сферы сила поверхностного натяжения, модуль которой \(~\Delta F = \alpha \Delta l\). Разложим вектор \(~\Delta \vec F\) на две составляющие силы \(~\Delta \vec F_1\) и \(~\Delta \vec F_2\). Из рисунка 2, а видим, что геометрическая сумма сил \(~\Delta \vec F_2\) для двух выделенных диаметрально противоположных элементов Δl равна нулю. Поэтому сила поверхностного натяжения направлена перпендикулярно плоскости сечения внутрь жидкости (рис. 2, в) и модуль ее равен

\(~F = \sum \Delta F_1 = \sum \Delta F \sin \alpha = \sum \alpha \Delta l \frac rR = \frac{\alpha r}{R} \sum \Delta l = \frac{\alpha r}{R} \cdot 2 \pi r = \frac{2 \alpha \pi r^2}{R} .\)

Избыточное давление, создаваемое этой силой\[~p = \frac FS\], где S = πr² — площадь основания сферического сегмента. Поэтому

\(~p = \frac{2 \alpha \pi r^2}{R \cdot \pi r^2} = \frac{2 \alpha}{R} .\)

Если поверхность жидкости вогнутая, то сила поверхностного натяжения направлена из жидкости (рис. 2, б) и давление под вогнутой поверхностью жидкости меньше, чем под плоской, на ту же величину \(~p = \frac{2 \alpha}{R}\) . Эта формула определяет лапласово давление для случая сферической формы свободной поверхности жидкости. Она является частным случаем формулы Лапласа, определяющей избыточное давление для произвольной поверхности жидкости двоякой кривизны:

\(~p = \alpha \left( \frac{1}{R_1} + \frac{1}{R_2} \right),\)

где R₁ и R₂ — радиусы кривизны двух любых взаимно перпендикулярных нормальных сечений поверхности жидкости. Радиус кривизны положителен, если центр кривизны соответствующего сечения находится внутри жидкости, и отрицателен, если центр кривизны находится вне жидкости. Для цилиндрической поверхности (R₁ = l; R₂ = ∞) избыточное давление \(~p = \frac{\alpha}{R}\) .

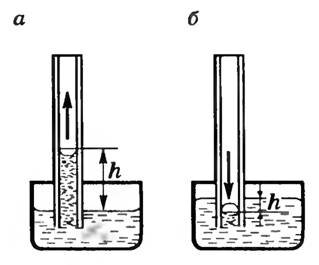
Если поместить узкую трубку (капилляр) одним концом в жидкость, налитую в широкий сосуд, то вследствие наличия силы лапласова давления жидкость в капилляре поднимается (если жидкость смачивающая) или опускается (если жидкость несмачивающая) (рис. 3, а, б), так как под плоской поверхностью жидкости в широком сосуде избыточного давления нет.

Рис. 3

Явления изменения высоты уровня жидкости в капиллярах по сравнению с уровнем жидкости в широких сосудах называются капиллярными явлениями.

Жидкость в капилляре поднимается или опускается на такую высоту h, при которой сила гидростатического давления столба жидкости уравновешивается силой избыточного давления, т.е.

\(~\frac{2 \alpha}{R} = \rho gh .\)

Откуда \(~h = \frac{2 \alpha}{\rho gR}\). Если смачивание не полное θ ≠ 0 (θ ≠ 180°), то, как показывают расчеты, \(~h = \frac{2 \alpha}{\rho gR} \cos \theta\).

Капиллярные явления весьма распространены. Поднятие воды в почве, система кровеносных сосудов в легких, корневая система у растений, фитиль и промокательная бумага — капиллярные системы.

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 182-184.