Т. Скорость молекул газа

Измерение скоростей газовых молекул. Опыт Штерна. Распределение Максвелла

Из формул \(~\mathcal h W_K \mathcal i = \frac 32 kT\) и \(~\mathcal h W_K \mathcal i = \frac{m_0 \mathcal h \upsilon^2 \mathcal i}{2}\) получаем формулу для расчета средней квадратичной скорости движения молекул одноатомного газа:

\(~\mathcal h \upsilon_{KB} \mathcal i = \sqrt{\mathcal h \upsilon^2 \mathcal i} = \sqrt{\frac{3kT}{m_0}} = \sqrt{\frac{3RT}{M}} , \qquad (1)\)

так как \(~m_0 = \frac{M}{N_A}\) и \(~kN_A = R\), где R — универсальная газовая постоянная.

Таким образом \(~\mathcal h \upsilon_{KB} \mathcal i\) зависит от температуры и природы газа. Так, при 0 °С для водорода она равна 1800 м/с. для азота — 500 м/с.

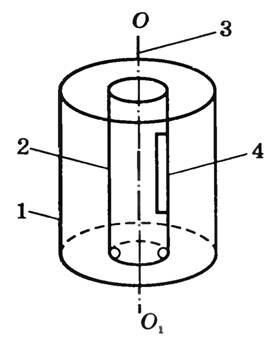
Впервые на опыте определил скорость молекул О. Штерн. В камере, из которой откачан воздух, находятся два коаксиальных цилиндра 1 и 2 (рис. 1), которые могут вращаться вокруг оси OO₁ с постоянной угловой скоростью ω.

Рис. 1

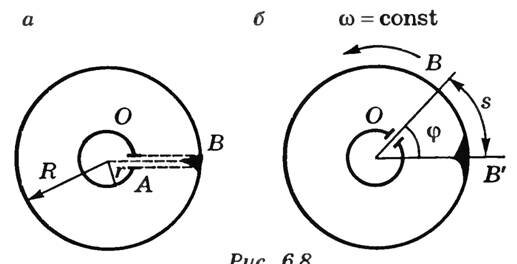
Вдоль оси OO₁ натянута платиновая посеребренная проволока, через которую пропускают электрический ток. Она нагревается, и серебро испаряется. Атомы серебра через щель 4 в стенке цилиндра 2 попадают в цилиндр 1 и оседают на его внутренней поверхности, оставляя след в виде узкой полоски, параллельной щели. Если цилиндры неподвижны, то полоска расположена напротив щели (точка В на рис. 2, а) и имеет одинаковую толщину.

Рис. 2

При равномерном вращении цилиндра с угловой скоростью ω полоска смещается в сторону, противоположную вращению, на расстояние s относительно точки В (рис. 2, б). На такое расстояние сместилась точка В цилиндра 1 за время t, которое необходимо, чтобы атомы серебра прошли расстояние, равное R - r, где R и r — радиусы цилиндров 1 и 2.

\(~s = \upsilon_1 t = \omega Rt ,\)

где υ₁ — линейная скорость точек поверхности цилиндра 1. Отсюда

\(~t = \frac{s}{\omega R} .\)

Скорость атомов серебра

\(~\upsilon = \frac{R - r}{t} = \frac{\omega(R - r)R}{s} .\)

Зная R, r, ω и измерив экспериментально s, по этой формуле можно рассчитать среднюю скорость движения атомов серебра. В опыте Штерна υ ~ 650 м/с. Это значение совпадает с теоретическим значением средней квадратичной скорости молекул. Это служит экспериментальным доказательством справедливости формулы (1), а следовательно, и формулы (3).

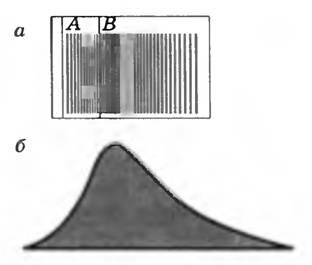
В опыте Штерна было обнаружено, что ширина полоски на поверхности вращающегося цилиндра гораздо больше геометрического изображения щели и толщина ее в разных местах неодинакова (рис. 3, а). Это можно объяснить только тем, что атомы серебра движутся с различными скоростями. Атомы, летящие с некоторой скоростью, попадают в точку В’. Атомы, летящие быстрее, попадают в точку, лежащую на рисунке 2 выше точки В’, а летящие медленнее, — ниже точки В’. Таким образом, каждой точке изображения соответствует определенная скорость, которую достаточно просто определить из опыта. Этим и объясняется то, что толщина слоя атомов серебра, осевших на поверхности цилиндра, не везде одинакова. Наибольшая толщина в средней части слоя, а по краям толщина уменьшается.

Рис. 3

Изучение формы сечения полоски осевшего серебра с помощью микроскопа показало, что она имеет вид, примерно соответствующий изображенному на рисунке 3, б. По толщине отложившегося слоя можно судить о распределении атомов серебра по скоростям.

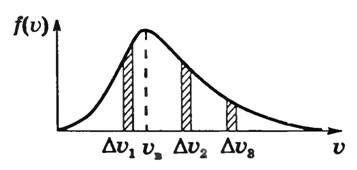
Разобьем весь интервал измеренных на опыте скоростей атомов серебра на малые Δυ. Пусть υ — одна из скоростей этого интервала. По плотности слоя подсчитаем число ΔN атомов, имеющих скорость в интервале от υ до υ + Δυ, и построим график функции \(~f(\upsilon) = \frac{\Delta N}{N \Delta \upsilon}\) , где Ν — общее число атомов серебра, осевших на поверхности цилиндра. Получим кривую, изображенную на рисунке 4. Она называется функцией распределения молекул по скоростям.

Рис. 4

Площадь заштрихованной площадки равна \(~\frac{\Delta N}{N \Delta \upsilon} \Delta \upsilon = \frac{\Delta N}{N}\) , т.е. равна относительному числу атомов, имеющих скорость в пределах υ + Δυ. Мы видим, что числа частиц, имеющих скорость из разных интервалов υ₁ + Δυ₁, υ₂ + Δυ₂, υ₃ + Δυ₃, резко различны. Существует какая-то скорость, около значения которой находятся скорости, с которыми движется наибольшее число молекул. Она называется наиболее вероятной скоростью υ_B, и ей соответствует максимум на рисунке 4. Эта кривая хорошо соответствует кривой, полученной Дж. Максвеллом, который, пользуясь статистическим методом, теоретически доказал, что в газах, находящихся в состоянии термодинамического равновесия, устанавливается некоторое, не меняющееся со временем, распределение молекул по скоростям, которое подчиняется вполне определенному статистическому закону, графически изображаемому кривой f(υ). Наиболее вероятная скорость, как показал Максвелл, зависит от температуры газа и массы его молекул по формуле \(~\mathcal h \upsilon_B \mathcal i = \sqrt{\frac{2RT}{M}}\).

Такому распределению подчиняются молекулы всевозможных веществ в различных состояниях при данной температуре. Если увеличить температуру (T₂ > T₁), то кривая (рис. 5) сместится вправо, наиболее вероятная скорость возрастет, появится больше быстрых частиц, уменьшится число медленных частиц и даже тех, которые движутся со скоростями, близкими к наиболее вероятной. Площади под кривыми будут одинаковыми, так как общее число частиц N не изменяется.

Зная закон изменения функции распределения молекул по скоростям f(υ), можно рассчитать среднюю, или среднюю арифметическую, скорость молекулы:

\(~\mathcal h \upsilon \mathcal i = \frac 1N \int \upsilon dN = \int^{\infty}_0 \upsilon F(\upsilon) d \upsilon .\)

Подставляя сюда значение F(υ) и интегрируя (в виду сложности F(υ) мы ее не приводим), получают

\(~\mathcal h \upsilon \mathcal i = \sqrt{\frac{8kT}{\pi m_0}} = \sqrt{\frac{8RT}{\pi M}} .\)

Среднее значение квадрата скорости

\(~\mathcal h \upsilon^2 \mathcal i = \frac 1N \int \upsilon^2 dN = \int^{\infty}_0 \upsilon^2 F(\upsilon) d \upsilon .\)

Средняя квадратичная скорость

\(~\mathcal h \upsilon_{KB} \mathcal i = \sqrt{\mathcal h \upsilon^2 \mathcal i} = \sqrt{\frac{3RT}{M}} .\)

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 134-136.