Т. Собственные колебания
Собственная частота колебаний в контуре
В идеальном колебательном контуре R =0. Поэтому полная энергия W остается постоянной в течение всего времени колебаний:
где q и I — мгновенные значения заряда конденсатора и силы тока в контуре. Производная по времени \(~w'(t)= 0\) (так как W=const) Следовательно,
Но \(~I = q',\) значит, \(~I' = q''.\) Поэтому
Обозначим \(~\frac 1{LC} = w_0^2,\) тогда \(~q'' = -w_0^2q\) или \(~q''+w_0^2q= 0\) — уравнение свободных электромагнитных колебаний в идеальном колебательном контуре.
Сравнивая это уравнение с уравнением \(~x'' + w^2x = 0,\) описывающим гармонические колебания, можно сделать вывод: свободные электромагнитные колебания в контуре (при R=0) являются гармоническими.
Решение этого уравнения имеет вид\[~q = q_0 \cos w_0 t,\] где q— начальное (амплитудное) значение заряда, сообщенного конденсатору; w — собственная циклическая частота свободных электромагнитных колебаний в контуре
Так как \(~T = \frac {2\pi}{w_0},\) то \(~T = 2\pi \sqrt {LC}\) — формула Томсона (период свободных электромагнитных колебаний в контуре).
Продифференцировав по времени выражение для заряда, найдем, что
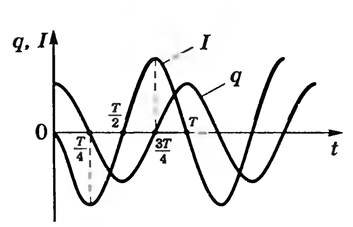
где \(~I_0 = q_0w_0\) — амплитудное значение силы тока. Следовательно, сила тока I в колебательном контуре совершает также гармонические колебания с той же частотой w, но по фазе они смещены на \(~\frac {\pi}2\) относительно колебаний заряда (рис. 3).
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 392-393.