Т. Теорема Гаусса

Теорема Остроградского—Гаусса и ее применение для расчета электростатических полей

Рис. 2

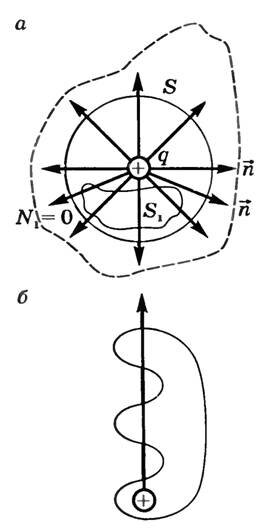
Пусть поле создается точечным электрическим зарядом q. Проведем замкнутую сферическую поверхность площадью S (рис. 2), окружающую этот заряд, центр которой совпадает с точкой нахождения заряда. Вычислим поток вектора напряженности через эту поверхность. За положительное направление нормали выберем направление внешней нормали \(~\vec n\). В этом случае во всех точках сферической поверхности E = const и cos α = 1.

Модуль напряженности поля на расстоянии R от заряда \(~E = \frac{q}{4 \pi \varepsilon_0 \varepsilon R^2}\). Площадь поверхности сферы \(~S = 4 \pi R^2\).

Следовательно, поток вектора напряженности через сферическую поверхность

\(~N_S = \frac{q 4 \pi R^2}{4 \pi \varepsilon_0 \varepsilon R^2} = \frac{q}{\varepsilon_0 \varepsilon} .\)

Полученный результат будет справедлив и для поверхности произвольной формы, а также при любом расположении заряда внутри этой поверхности. Действительно, если окружить сферу произвольной замкнутой поверхностью (рис. 2, а — поверхность изображена штрихами), то каждая линия напряженности, пронизывающая сферу, пройдет и сквозь эту поверхность.

Если замкнутая поверхность произвольной формы охватывает заряд (рис. 2, б), то при пересечении любой выбранной линии напряженности с поверхностью она то входит в поверхность, то выходит из нее. Нечетное число пересечений при вычислении потока в конечном счете сводится к одному пересечению, так как поток считается положительным, если линии напряженности выходят из поверхности, и отрицательным для линии, входящей в поверхность. Если же внутри поверхности площадью S₁ (см. рис. 2) заряды отсутствуют, то поток напряженности через эту поверхность равен нулю (N_S = 0).

Рис. 3

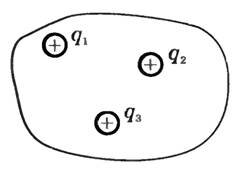
Если рассматриваемая поверхность охватывает не один, а несколько электрических зарядов, то под q следует понимать алгебраическую сумму этих зарядов (рис. 3) и

\(~N_S = \frac{q_1 + q_2 + q_3}{\varepsilon_0 \varepsilon} .\)

Эта формула выражает теорему Остроградского—Гаусса: поток вектора напряженности через замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на произведение электрической постоянной и диэлектрической проницаемости среды.

Применим эту теорему для расчета электростатических полей некоторых проводников.

Равномерно заряженная бесконечная плоскость

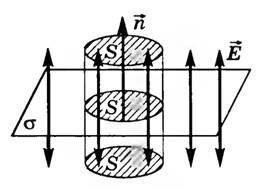
Пусть σ — поверхностная плотность заряда на плоскости (рис. 4).

Рис. 4

В качестве поверхности площадью S выберем цилиндрическую поверхность, образующая которой перпендикулярна плоскости. Основания этого цилиндра расположены перпендикулярно линиям напряженности по обе стороны от плоскости. Так как образующие цилиндра параллельны линиям напряженности (α = 90°, cos α = 0), то поток через боковую поверхность цилиндра отсутствует, и полный поток через поверхность цилиндра равен сумме потоков через два основания: N = 2ES. Внутри цилиндра заключен заряд q = σS, поэтому, согласно теореме Остроградского-Гаусса, \(~2ES = \frac{\sigma S}{\varepsilon_0 \varepsilon}\), где ε = 1 (для вакуума), откуда следует, что напряженность поля равномерно заряженной бесконечной плоскости

\(~E = \frac{\sigma}{2 \varepsilon_0 \varepsilon} .\)

Бесконечная равномерно заряженная нить

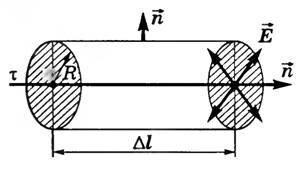
Пусть τ — линейная плотность заряда нити. Выделим участок нити длиной Δl и окружим его цилиндрической поверхностью, расположенной так, что ось цилиндра совпадает с нитью (рис. 5).

Рис. 5

Линии напряженности электростатического поля, создаваемого нитью в сечении, перпендикулярном самой нити, направлены перпендикулярно боковой поверхности цилиндра, поэтому поток напряженности сквозь боковую поверхность \(~N = E \cdot 2 \pi R \Delta l\), где R — радиус цилиндра. Через оба основания цилиндра поток напряженности равен нулю (α = 90°, cos α = 0). Тогда полный поток напряженности через выделенный цилиндр

\(~N = E \cdot 2 \pi R \Delta l .\)

Заряд, находящийся внутри этого цилиндра, q = τ · Δl.

Согласно теореме Остроградского—Гаусса, можно записать \(~E \cdot 2 \pi R \Delta l = \frac{\tau \Delta l}{\varepsilon_0 \varepsilon}\) . Следовательно, модуль напряженности поля, создаваемого равномерно заряженной бесконечно длинной нитью на расстоянии R от нее,

\(~E = \frac{\tau}{2 \pi \varepsilon_0 \varepsilon R} .\)

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 220-222.