Умножение вектора
Умножение вектора на скаляр
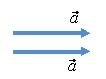
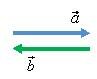
Найдем сумму двух векторов \(\vec a\) (рис. 1, а). Получился вектор \(\vec c = \vec a+\vec a\), направленный так же, как и вектор \(\vec a\), и модуль которого равен \(2a \,\), т.е. \(\vec c = 2\vec a\) (рис. 1, б). Если сложить k векторов \(\vec a\), то получится вектор \(\vec c = \underbrace {\vec a + \vec a + \ldots + \vec a}_{k}\), направленный в ту же сторону, что и вектор \(\vec a\), и имеющий модуль \(k \cdot a\), т.е. \(\vec c = k \cdot \vec a\).
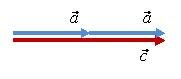
Рассмотрим вектор \(\vec b = -1 \cdot \vec a\). Вектор \(\vec b\) будет направлен в сторону, противоположную вектору \(\vec a\), а модуль его будет равен а (рис. 2, а).
Если сложить k векторов \(\vec b\), то получится вектор \(\vec d = \underbrace {\vec b + \vec b + \ldots + \vec b}_{k}\), направленный в ту же сторону, что и вектор \(\vec b\), и модуль которого равен \(k \cdot b\), т.е. \(\vec d = k \cdot \vec b\) (рис. 2, б).
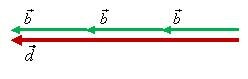
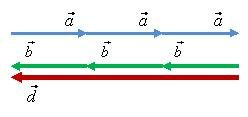
Так как \(\vec b = -\vec a\) , то \(\vec d = -k \cdot \vec a\) (рис. 2, в). Из рисунка видно, что вектор \(\vec d\) направлен в сторону, противоположную направлению вектора \(\vec a\), и модуль его равен \(k \cdot a\).
Обобщая выше сказанное, можно сделать вывод, что
при умножении вектора \(\vec a\) на скаляр k получаем вектор \(\vec c = k \cdot \vec a\), модуль которого равен \(k \cdot a\), и направленный
- в ту же сторону, что и вектор \(\vec a\), если скаляр \(k > 0\,\);
- в сторону, противоположную направлению вектора \(\vec a\), если скаляр \(k < 0\,\).
Произведение векторов
Различают скалярное и векторное произведение векторов.
1. При скалярном умножении векторов \(\vec a\) и \(\vec b\) получается такой скаляр с, что \(c = a \cdot b \cdot \cos \alpha\), где \(\alpha\,\) – угол между векторами \(\vec a\) и \(\vec b\).
Применяются следующие способы обозначения скалярного произведения\[\vec a \cdot \vec b\] или \(\left ( \vec a , \vec b \right )\).
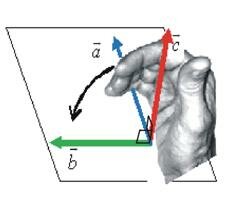
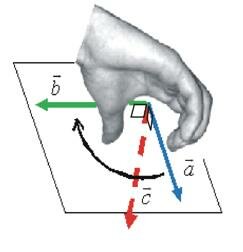
2. При векторном произведении векторов \(\vec a\) и \(\vec b\) получается такой вектор \(\vec c\), что его модуль равен \(c = a \cdot b \cdot \sin \alpha\), где \(\alpha\,\) – угол между векторами \(\vec a\) и \(\vec b\).
Применяются следующие способы обозначения векторного произведения\[\vec a \times \vec b\] или \(\left [ \vec a , \vec b \right ]\).
Направлен вектор \(\vec c\) так, что он перпендикулярен плоскости, в которой лежат вектора \(\vec a\) и \(\vec b\), и совпадает с поступательным движением правого винта (правой руки) при его повороте от \(\vec a\) к \(\vec b\) на угол меньший \(\pi\,\) (рис. 6).