A. Закон Паскаля
Гидростатическое давление
Рассмотрим равновесие однородной жидкости, находящейся в поле тяготения Земли.
На каждую частицу жидкости, находящейся в поле тяготения Земли, действует сила тяжести. Под действием этой силы каждый слой жидкости давит на расположенные под ним слои. В результате давление внутри жидкости на разных уровнях не будет одинаковым. Следовательно, в жидкостях существует давление, обусловленное ее весом.
Давление, обусловленное весом жидкости, называют гидростатическим давлением.
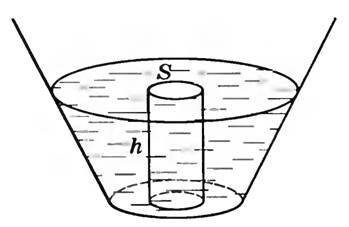
Для количественного расчета мысленно выделим в жидкости малый объем цилиндрической формы, расположенный вертикально, сечением S и высотой h (рис. 2). В случае неподвижной жидкости вес этого цилиндра, а значит, и сила давления на площадку S в основании будет равна силе тяжести \(~m \vec g\).
Тогда давление на площадку
\(~p = \rho gh\) — гидростатическое давление, где ρ — плотность жидкости, h — высота столба жидкости. Таким образом, гидростатическое давление равно весу столба жидкости с единичным основанием и высотой, равной глубине погружения точки под свободной поверхностью жидкости.
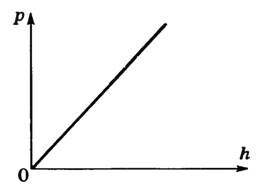
Графически зависимость давления от глубины погружения в жидкость представлена на рисунке 3.
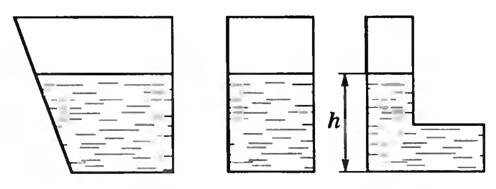
Давление жидкости на дно не зависит от формы сосуда, а определяется только высотой уровня жидкости и ее плотностью. Во всех случаях, приведенных на рисунке 4, давление жидкости на дно сосудов одинаково.
Жидкость давит на данной глубине одинаково по всем направлениям — не только вниз, но и вверх, и в стороны.
Следовательно, давление на стенку на данной глубине будет таким же, как и давление на горизонтальную площадку, расположенную на той же глубине.
Если над свободной поверхностью жидкости создается давление p0 то давление в жидкости на глубине будет
Обратите внимание на различие выражений: "давление жидкости на глубине h" (p = pgh) и "давление в жидкости на глубине h" (p = p0 + pgh). Это надо учитывать при решении различных задач.
Силы давления на дно и на стенки можно рассчитать по формулам\[~F_d = \rho gh S_d\] — сила давления жидкости на горизонтальное дно, где Sd — площадь дна;
\(~F_{st} = \frac{\rho gh}{2} S_{st}\) — сила давления жидкости на боковую прямоугольную вертикальную стенку сосуда, где Sst — площадь стенки.
В покоящейся жидкости свободная поверхность жидкости всегда горизонтальна.
Нередко встречаются случаи, когда жидкость, покоясь относительно сосуда, движется вместе с ним. Если при этом сосуд движется равномерно и прямолинейно, то свободная поверхность жидкости будет горизонтальна. Но если сосуд движется с ускорением, то ситуация меняется и возникают вопросы о форме свободной поверхности жидкости, о распределении давления в ней.
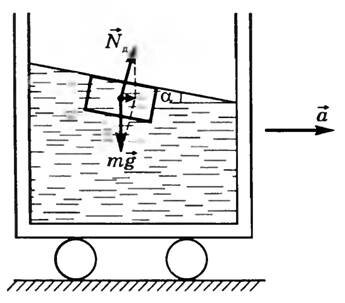
Так, в случае горизонтального движения сосуда с ускорением \(~\vec a\) в поле тяготения Земли любая часть жидкости массой m движется с тем же ускорением \(~\vec a\) под действием равнодействующей силы давления \(~\vec N_d\), действующей со стороны остальной жидкости и силы тяжести \(~m \vec g\) (рис. 5).
Основное уравнение динамики:
В результате свободная поверхность жидкости не будет горизонтальна, а образует с горизонтом угол α, который можно легко найти, если спроецировать а основное уравнение динамики на горизонтальную и вертикальную оси\[~N_d \sin \alpha = ma; \ N_d \cos \alpha = mg\]. Отсюда
Давление на горизонтальную поверхность (горизонтальное дно) будет возрастать в направлении, противоположном ускорению.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 95-97.